WeiMao-2019-LearningTrajectoryDependenciesForHumanMotionPrediction-ICCV

# Learning Trajectory Dependencies for Human Motion Prediction #paper

---

1. paper-info

1.1 Metadata

• Author:: [[Wei Mao]], [[Miaomiao Liu]], [[Mathieu Salzmann]], [[Hongdong Li]]
• 作者机构::
• Keywords:: #HMP, #GAN , #DCT
• Journal:: #ICCV (oral)
• Date:: [[2020-07-06]]
• 状态:: #Done
• 链接:: http://arxiv.org/abs/1908.05436
• 修改时间:: 2022.11.23

1.2. Abstract

Human motion prediction, i.e., forecasting future body poses given observed pose sequence, has typically been tackled with recurrent neural networks (RNNs). However, as evidenced by prior work, the resulted RNN models suffer from prediction errors accumulation, leading to undesired discontinuities in motion prediction. In this paper, we propose a simple feed-forward deep network for motion prediction, which takes into account both temporal smoothness and spatial dependencies among human body joints. In this context, we then propose to encode temporal information by working in trajectory space, instead of the traditionally-used pose space. This alleviates us from manually defining the range of temporal dependencies (or temporal convolutional filter size, as done in previous work). Moreover, spatial dependency of human pose is encoded by treating a human pose as a generic graph (rather than a human skeletal kinematic tree) formed by links between every pair of body joints. Instead of using a pre-defined graph structure, we design a new graph convolutional network to learn graph connectivity automatically. This allows the network to capture long range dependencies beyond that of human kinematic tree. We evaluate our approach on several standard benchmark datasets for motion prediction, including Human3.6M, the CMU motion capture dataset and 3DPW. Our experiments clearly demonstrate that the proposed approach achieves state of the art performance, and is applicable to both angle-based and position-based pose representations. The code is available at https://github.com/wei-mao-2019/LearnTrajDep

---

2. Methods

Fig.1. 网络结构

Source:

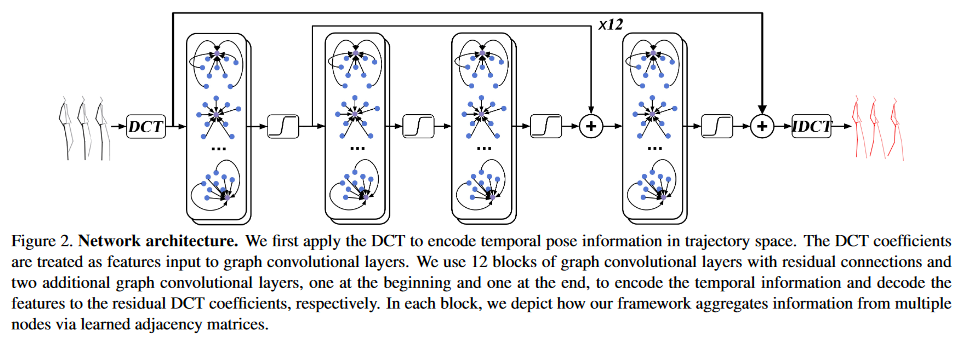
上图对文章的模型进行了展示和说明。输如历史动作序列，经过DCT编码之后， 送入由图卷积组成的网络结构中，然后在经过IDCT解码，得到历史输出。
历史动作序列又两种表示方式，基于角度的和基于3D坐标的，作者给出了对两种表示的结果分析，结果表明3D坐标表示性能更好。
在之前，都是对人体结构建模，而作者则将动作序列看做各个关节点的轨迹运动。为了处理时间维度的信息，作者使用DCT，对时间维度的信息进行编码。此外，为了处理空间维度的信息，作者采用了图卷积神经网络。

2.1 DCT-based Temporal Encoding

Our temporal encoding aims to capture the motion pattern of each joint.

该基于DCT的时间编码是为了处理单个关节点的轨迹的。使用\(\tilde{X}_k=(x_{(k,1)},x_{(k,2)},...,x_{(k,N)})\) 来表示第\(k\)个关节点穿过\(N\)帧的轨迹。作者在此处使用了一种基于Discrete Cosine Transfrom(DCT)的轨迹表征方法。之所以使用该方法，是因为DCT编码可以丢掉那些高频率的信息(在图像上表现为那些细微特征)，这样可以得到更加紧凑的轨迹表征方式，也就可以捕捉到动作序列的连续性。
给定一个轨迹\(\tilde{X}_k\)，其对应的DCT系数可以通过下面的公式进行计算，

\[C_{k, l}=\sqrt{\frac{2}{N}} \sum_{n=1}^{N} x_{k, n} \frac{1}{\sqrt{1+\delta_{l 1}}} \cos \left(\frac{\pi}{2 N}(2 n-1)(l-1)\right) \]

其中\(\delta_{l 1}\)为克罗内克函数：

\[\delta_{i j}=\left\{\begin{array}{ll} 1 & \text { if } i=j \\ 0 & \text { if } i \neq j \end{array}\right.\]

\(l\in \{1,2,...,N\}\) 。
在给定\(C_{k,l}\)时也可以通过IDCT计算出对应的轨迹信息\(\tilde{X}_k\)，计算公式如下：

\[x_{k, n}=\sqrt{\frac{2}{N}} \sum_{l=1}^{N} C_{k, l} \frac{1}{\sqrt{1+\delta_{l 1}}} \cos \left(\frac{\pi}{2 N}(2 n-1)(l-1)\right) \]

上面给出了一个关节点的编码方式，总的来说，若有\(K\)个关节点，则历史序列可以表示为一个\(K\times l\)的矩阵。
有了上面的分析，就可以将原动作预测问题(\(X_{1:N}-->X_{N+1, N+T}\))看做给定\(K\times l ;\ matrix\)去 预测下一个\(K\times l\)矩阵的问题。

注意： 基于zero-velocity baseline[1]，加入了残差连接。

2.2 Graph Convolutional Layer

DCT方法可以解决时间维度的信息，而空间上面的信息无法保证，在本paper中，作者使用了GCN-based的网络结构来处理空间维度的信息。不同于传统的GCN网络结构，本文中的计算方式为：

\[\mathbf{H}^{(p+1)}=\sigma\left(\mathbf{A}^{(p)} \mathbf{H}^{(p)} \mathbf{W}^{(p)}\right) \]

\(A \ and \ (W\in(256\times 256))\)都是可学习的参数矩阵。

Using a different learnable A for every graph convolutional layer allows the network to adapt the connectivity for different operations.

具体的网络结构就如Fig.1所示，包含12个残差块，每个残差块由2个图卷积层构成。在网络开始和结束也各自有一层图卷积层。

2.3 Loss Function

无论用那种表示方式，最后的损失函数都可看做重构损失。

1. angles-based

\[\ell_{a}=\frac{1}{(N+T) K} \sum_{n=1}^{N+T} \sum_{k=1}^{K}\left|\hat{x}_{k, n}-x_{k, n}\right| \]

2. 3D 坐标

\[\ell_{m}=\frac{1}{(N+T) J} \sum_{n=1}^{N+T} \sum_{j=1}^{J}\left||\hat{p}_{j, n}-p_{j, n}\right|| ^2 \]

3. Experiments

• datasets
  • Human3.6m
  • CMU-Mocap
  • 3DPW
• Metrics
  • MPJPE(Mean Per Joint Position Error)
• optimzer
  • ADAM

4. Conclusion

最突出的创新点，将人体运动看做各关节点的轨迹，经过DCT编码，抛掉高频率的特征后，可以得到更加平滑的动作序列。
其次，用GCN来处理空间信息。

---