YeYuan-2021-AgentFormer-AgentAwareTransformers for Socio-Tempolar Multi-Agent Forecasting-ICCV

# AgentFormer: Agent-Aware Transformers for Socio-Temporal Multi-Agent Forecasting #paper

---

1. paper-info

1.1 Metadata

• Author:: [[Ye Yuan]], [[Xinshuo Weng]], [[Yanglan Ou]], [[Kris M. Kitani]]
• 作者机构:: Carnegie Mellon University
• Keywords:: #MutilpleAgents , #Transformer , #CVAE
• Journal:: #ICCV
• Date:: [[2021]]
• 状态:: #Doing
• 链接:: https://openaccess.thecvf.com/content/ICCV2021/html/Yuan_AgentFormer_Agent-Aware_Transformers_for_Socio-Temporal_Multi-Agent_Forecasting_ICCV_2021_paper.html

1.2 Abstract

Predicting accurate future trajectories of multiple agents is essential for autonomous systems but is challenging due to the complex interaction between agents and the uncertainty in each agent’s future behavior. Forecasting multiagent trajectories requires modeling two key dimensions: (1) time dimension, where we model the influence of past agent states over future states; (2) social dimension, where we model how the state of each agent affects others. Most prior methods model these two dimensions separately, e.g., first using a temporal model to summarize features over time for each agent independently and then modeling the interaction of the summarized features with a social model. This approach is suboptimal since independent feature encoding over either the time or social dimension can result in a loss of information. Instead, we would prefer a method that allows an agent’s state at one time to directly affect another agent’s state at a future time. To this end, we propose a new Transformer, termed AgentFormer, that simultaneously models the time and social dimensions. The model leverages a sequence representation of multi-agent trajectories by flattening trajectory features across time and agents. Since standard attention operations disregard the agent identity of each element in the sequence, AgentFormer uses a novel agent-aware attention mechanism that preserves agent identities by attending to elements of the same agent differently than elements of other agents. Based on AgentFormer, we propose a stochastic multi-agent trajectory prediction model that can attend to features of any agent at any previous timestep when inferring an agent’s future position. The latent intent of all agents is also jointly modeled, allowing the stochasticity in one agent’s behavior to affect other agents. Extensive experiments show that our method significantly improves the state of the art on wellestablished pedestrian and autonomous driving datasets.

1. 说明多智能体的轨迹预测问题很重要也面临挑战。
2. 预测多智能体的轨迹需要对两个维度进行建模：time dimension,social dimension
3. 之前的方法单独对这两个维度进行建模。（介绍之前的方法，引出本文方法）
4. 分开建模这些方法会造成信息的缺失。（之前方法的缺陷）
5. 提出了新方法，可以直接对两个维度进行建模分析。
6. 具体介绍方法：
   1. 提出了一种新的transformer--AgentFormer,能够同时对time和social维度进行建模。
      1. sequence representation
   2. 提出了新的注意力机制agent-aware attention mechanism。
   3. 根据1,2， 提出了stochastic multi-agent trajectory prediction model
   4. 在预测模型中也加入了latent intent of all agents
7. 方法性能优秀。

---

2. Introduction

• 问题： forecasting accurate future trajectstate of ohter agents
• 之前的方法：
  • temporal model和social model分开建模
  • 问题：分开建模的性能不是最优的。
  • 原因：
    1. independent feature encoding over either the time or social dimension is not informed by features across the other dimension.
    2. the encoded features may not contain the necessary information for modeling the other dimension.
• 作者的方法：
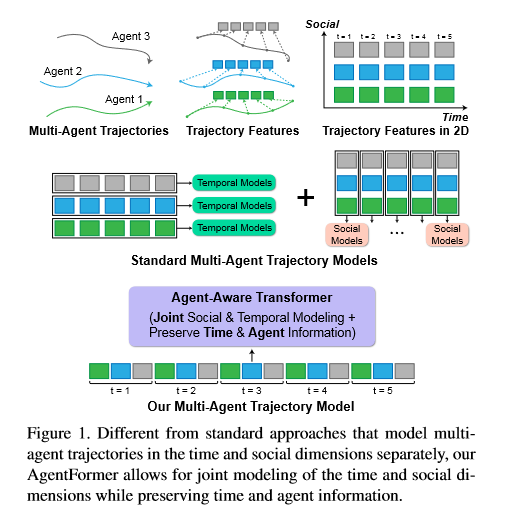
  1. new Transformer model--AgentFormer：能够同时学习time 和 social dimensions, 该transformer允许某个智能体能够直接影响到其他智能体的未来轨迹，而不是通过某个中间特征。
  2. sequence representation：transformer是以序列为输入的，所以作者提出了新的序列表示方法---跨时间和智能体的扁平化轨迹特征(Figure. 1)
     • 问题：如果直接使用Transformer的注意力机制会导致时间和智能体之间的信息丢失，因为标准的注意力操作会丢弃与序列中每个元素关键的时间步长和智能体标识。
  3. 解决2的问题方法：
     1. time encoder：对每个元素增加一个时间编码，保证时间信息不会丢失。
     2. a novel agent-aware attention mechanism：
        • 为什么不使用和time encoder一样的方法：因为在做智能体之间，没有固定的顺序，如果使用和time encoder一样的方法，会破坏多智能体之间的感知不变形(permutation invariance)，并且可能给多智能体之间添加人为依赖关系。
        • 新方法会产生两个key,queries 对，能够同时处理自己与其他智能体之间的关联信息。
          1. inter-agent attention(agent to agent)
          2. intra-agent attention(agent to itself)
        • masked operations：mask矩阵能够标识出没有关联的多智能体，计算注意力时可以更合理。
  4. multi-agent trajectory prediction framework
     • 基于CVAE
     • latent code： 能够对每个智能体的潜在意图编码。该潜在编码使用训练期间所以智能体的未来轨迹中共同推断出来的；也被用于预测多智能体的未来轨迹。
     • multi-agent trajectory sampler： 能够生成多样化和零花的多智能体轨迹。
• 模型评估：
  • dataset：
    • ETH
    • UCY
    • nuScenes
• contributions:
  1. new Transformer
  2. agent-aware attention mechanism
  3. multi-agent forecasting framework

Figure.1. sequence representation

Source: https://openaccess.thecvf.com/content/ICCV2021/html/Yuan_AgentFormer_Agent-Aware_Transformers_for_Socio-Temporal_Multi-Agent_Forecasting_ICCV_2021_paper.html

3. Approach

• \(X^t=(x_1^t,x_2^t,...,x_N^t)\)：\(1,2,,,N\)表示\(N\)个智能体，\(t\)表示当前时间步，\(X\)表示过去轨迹。
  • \(x_n^t \in \mathbb{R}^{d_s}\)：包含了智能体的位置，速度和(可选)头角度信息
• \(X=(X^{-H}, X^{-H+1},...,X^0)\)：多智能体在过去\(H+1\)个时间步的轨迹信息。
• \(Y^t = (y_1^t,y_2^t,...,y_N^t)\)：\(1,2,,,N\)表示\(N\)个智能体，\(t\)表示当前时间步，\(Y\)表示待预测轨迹。
• \(I\)：可选的上下文信息。(人行道，道路边界的注释)
• \(p_{\theta}(Y|X,I)\)：生成模型，\(\theta\)模型参数。

3.1 AgentFormer: Agent-Aware Transformers

与传统Transformer相比

• 共同点：都由encoder和decoder组成。
• 不同点：
  1. time encoder代替positional encoder
  2. agent-aware attention mechanism代替scaled dot-product attention
     Multi-Agent Trajectories as a Sequence
     过去的多智能体轨迹\(X=(x_1^{-H},...,x_N^{-H},x_1^{-H+1},...,x_N^{-H+1},x_1^{0},...,x_N^{0})\) (同Figure.1),\(X\)的长度\(L_p=N \times (H+1)\),(\(N\): 智能体数，\((H+1)\)：时间步长)
     未来的多智能体轨迹\(Y=(y_1^1,...,y_N^1,y_1^2,...,y_N^2,y_1^T,...,y_N^T,)\)，\(Y\)的长度\(L_f=N\times T\)
     如果直接用传统的注意力机制会产生两个问题(同2.Introduction)：

1. loss time information：时间信息没有处理
2. loss of agent information：多智能体之间不一定都由关联。
   解决办法：
3. time encoder
4. agent-aware attention
   time encoder
   同传统的positional encoding相似，同样使用正弦设计，只是用时间戳代替了位置。
   \(x_n^t\)对应的times-tamp feature\(\tau_n^t \in \mathbb{R}^{d_\tau}\):

\[\tau_{n}^{t}(k)=\left\{\begin{array}{ll} \sin \left((t+H) / 10000^{k / d_{\tau}}\right), & k \text { is even } \\ \cos \left((t+H) / 10000^{(k-1) / d_{\tau}}\right), & k \text { is odd } \end{array}\right. \]

\(k\)：时间戳
\(d_{\tau}\)：时间戳的特征维度
time encoder输出时间戳序列\(\bar{X} = (\bar{x}_1^t,...,\bar{x}_N^t), \bar{x}_N^t \in \mathbb{R}^{d_{\tau}}\) ;

\[\bar{x}_N^t=W_2(W_1x_n^t\oplus \tau_n^t) \]

\(W_1\in\mathbb{R}^{d_{\tau}\times d_s}\) and \(W_2\in\mathbb{R}^{d_{\tau}\times 2d_{\tau}}\)

Agent-Aware Attention
不同于传统的注意力机制，作者提出的注意力机制计算过程如下：

\[ \begin{align} AgentAwareAttention & (\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{softmax}\left(\frac{\mathbf{A}}{\sqrt{d_{k}}}\right) V \tag{1} \\ \mathbf{A}&=\mathbf{M} \odot\left(\mathbf{Q}_{\text {self }} \mathbf{K}_{\text {self }}^{T}\right)+(1-\mathbf{M}) \odot\left(\mathbf{Q}_{o t h e r} \mathbf{K}_{\text {other }}^{T}\right) \tag{2}\\ \mathbf{Q}_{\text {self }}&=\mathbf{Q W}_{\text {self }}^{Q}, \quad \mathbf{K}_{\text {self }}=\mathbf{K W}_{\text {self }}^{K} \tag{3} \\ \mathbf{Q}_{o t h e r}&=\mathbf{Q} \mathbf{W}_{o t h e r}^{Q}, \quad \mathbf{K}_{o t h e r}=\mathbf{K} \mathbf{W}_{\text {other }}^{K} \tag{4} \\ \end{align} \]

\(K\),\(V\)： 过去序列\(X \in \mathbb{R}^{L_p\times d_s}\)
\(Q\)：未来轨迹序列\(Y\in mathbb{R}^{L_f\times d_p}\)
\(K_{self},K_{other} \in \mathbb{R}^{L_p\times d_k}\)
\(Q_{self},Q_{other}\in\mathbb{R}^{L_f\times d_k}\)
\(M\in \mathbb{R}^{L_f\times L_p}\)：mask 矩阵，定义如下：

\[M_{ij}=\mathbb{1}(i \bmod N =j \bmod N ) \]

如figure.2 所示，如果\(q_i\)和\(k_j\)为相同的智能体，就只许计算intra-agent attention，反之则计算inter-agent attention。

Figure.2 Illustration of agent-aware attention

Source: https://openaccess.thecvf.com/content/ICCV2021/html/Yuan_AgentFormer_Agent-Aware_Transformers_for_Socio-Temporal_Multi-Agent_Forecasting_ICCV_2021_paper.html

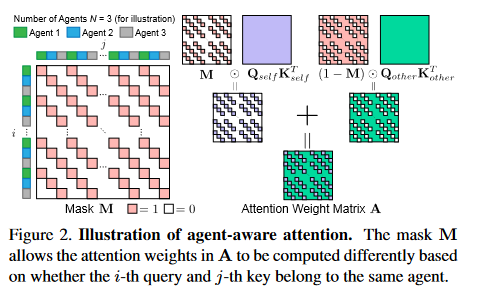
上面只说明了单头注意力机制的过程，也可以用于多头计算。

Encoding Agent Connectivity
也可以将智能体之间的联系关系考虑进去，
如果智能体\(n\)和\(m\)之间的距离\(D_{nm}\)在当前时间步小于一个阈值\(\eta\),则说明两者之间有联系，反之没有联系，则将\(A_{ij}=-\infty\)

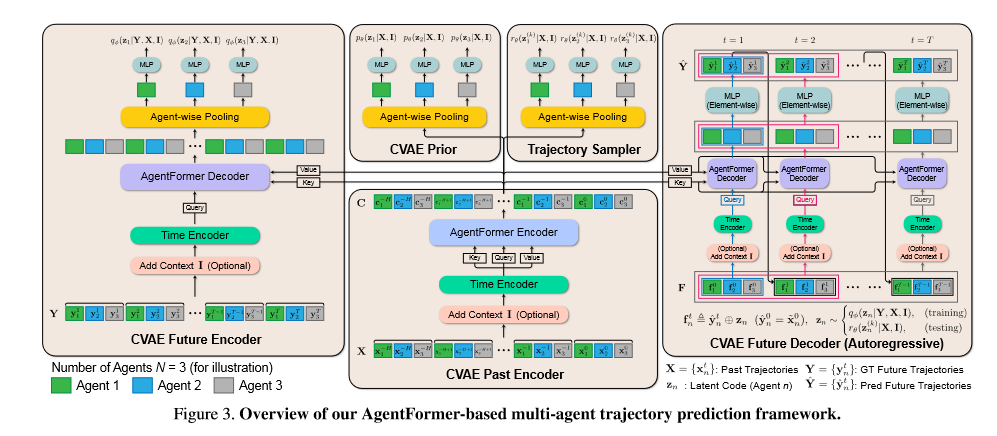
3.2 Multi-Agent Prediction with AgentFormer

该模型在CVAE的基础之上加入了自鞥难题的潜在意图变量\(Z=\{z_1,...,z_N\}\)
未来轨迹分布：

\[p_{\theta}(\mathbf{Y} \mid \mathbf{X}, \mathbf{I})=\int p_{\theta}(\mathbf{Y} \mid \mathbf{Z}, \mathbf{X}, \mathbf{I}) p_{\theta}(\mathbf{Z} \mid \mathbf{X}, \mathbf{I}) d \mathbf{Z} \]

loss function :

\[\begin{aligned} \mathcal{L}_{\text {elbo }}=&-\mathbb{E}_{q_{\phi}(\mathbf{Z} \mid \mathbf{Y}, \mathbf{X}, \mathbf{I})}\left[\log p_{\theta}(\mathbf{Y} \mid \mathbf{Z}, \mathbf{X}, \mathbf{I})\right] \\ &+\mathbf{K L}\left(q_{\phi}(\mathbf{Z} \mid \mathbf{Y}, \mathbf{X}, \mathbf{I}) \| p_{\theta}(\mathbf{Z} \mid \mathbf{X}, \mathbf{I})\right) \end{aligned} \]

model architecture

Figure.3.

Source: https://openaccess.thecvf.com/content/ICCV2021/html/Yuan_AgentFormer_Agent-Aware_Transformers_for_Socio-Temporal_Multi-Agent_Forecasting_ICCV_2021_paper.html

Encoding Context (Semantic Map)
从上下文信息\(I\)中提取出额外的视觉特征\(v_n\) (\(I_n\in \mathbb{R}^{H\times W\times C}\)),通过一个卷积神经网络。
CVAE Past Encoder
输入：past trajectory sequence X
输出：feature sequence\(C=(c_1^{-H},...,C_N^{-H},c_1^{-H+1},...,C_N^{-H+1},c_1^{0},...,C_N^{0},)\)
CVAE Prior
通过agent-wise pooling将CVAE Past Encoder输出的\(C\)进行平均池化，（对每一个智能体）

\[C_n=mean(c_n^{-H},...,c_n^0) \]

在通过多层感知机将\(C_n\)映射成Gaussian parameters\((\mu _n^p,\sigma _n^p)\) ,从而得到\(z_n\)的先验分布

\[p_{\theta}(z_n|X, I) = \mathcal{N}(\mu _n^p,Diag(\sigma _n^p)) \]

这里的\(p_{\theta}(z_n|X,I)\) 近似于 \(q_{\varphi}(z_n|Y,X,I)\)

CVAE Future Encoder
该结构同CVAE Past Encoder+CVAE Prior，只是注意力机制有所不同，学习\(z_n\)的近似后验分布

\[q_{\varphi}(z_n|Y,X,I)=\mathcal{N}(\mu _n^q,Diag(\sigma _n^q)) \]

CVAE Future Decoder
不同于传统的Transformer，这里的结构为autoregressive。具体流程如Figure.3

Trajectory Sampler
采用一种多样性采样技术DLow[note] ,通过该技术，可以生成多样性的多轨迹序列。该采样过程很生成\(K\)个latent code\(\{Z^{(1)},...,Z^{(K)}\}\),其中\(Z^{k}=\{z_1^{k},...,z_N^{k}\}\)
trajectory samples loss：

\[\begin{array}{l} \mathcal{L}_{\text {samp }}=\min _{k}\left\|\hat{\mathbf{Y}}^{(k)}-\mathbf{Y}\right\|^{2} \\ +\sum_{n=1}^{N} \mathrm{KL}\left(r_{\theta}\left(\mathbf{z}_{n}^{(k)} \mid \mathbf{X}, \mathbf{I}\right) \| p_{\theta}\left(\mathbf{z}_{n} \mid \mathbf{X}, \mathbf{I}\right)\right) \\ +\frac{1}{K(K-1)} \sum_{k_{1}=1}^{K} \sum_{k_{1} \neq k_{2}}^{K} \exp \left(-\frac{\left\|\hat{\mathbf{Y}}^{\left(k_{1}\right)}-\hat{\mathbf{Y}}^{\left(k_{2}\right)}\right\|^{2}}{\sigma_{d}}\right) \end{array} \]

4. Experiments

• datasets
  • ETH
  • UCY
  • nuScenes
• Metrics
  • minimum average displacement error\(ADE_K\)
    • \(\mathrm{ADE}_{K}=\frac{1}{T} \min _{k=1}^{K} \sum_{t=1}^{T}\left\|\hat{\mathbf{y}}_{n}^{t,(k)}-\mathbf{y}_{n}^{t}\right\|^{2}\)
  • final displacement error\(FDE_K\)
    • \(FDE_K=\min _{k=1}^{K}\left\|\hat{\mathbf{y}}_{n}^{T,(k)}-\mathbf{y}_{n}^{T}\right\|^{2}\)

5. 总结

本文方法同时处理time dimension和social dimension，time dimension利用和position encoding类似的编码方式对时间维度进行编码，而social dimension利用一种新的注意力机制对输入的序列进行处理，新的注意力机制能够很好地处理智能体与智能体之间和智能体与其他智能体之间的联系，本质上是transformer的变种。
在Transformer的基础上加入了CVAE,可以达到多样化生成的效果。