江苏科技大学大二《数据结构》课内实验报告模板答案

江苏科技大学

《数据结构》实验报告

（2024/2025学年第1学期）

学生姓名：

学生学号：

院 系： 计算机学院

专 业：

考核得分：

2024 年 12 月

实验一 线性表的操作

一、实验目的

掌握线性表的基本操作在存储结构上的实现，其中以单链表的操作作为重点。

二、实验题目

1.以单链表作为存储结构，实现线性表的就地逆置。

2. 创建一个非递减序（有重复值）的单链表，实现删除值相同的多余结点。

三、实验预习的核心算法伪代码

· 单链表就地逆置

reverseList(head):

prev = NULL

curr = head

while curr != NULL:

next = curr.next

curr.next = prev

prev = curr

curr = next

head = prev

删除重复节点

removeDuplicates(head):

current = head

while current != NULL:

runner = current

while runner.next != NULL:

if runner.next.value == current.value:

runner.next = runner.next.next

else:

runner = runner.next

current = current.next

四、实验源程序

单链表逆置

#include

using namespace std;

struct Node {

int data;

Node* next;

Node(int value) : data(value), next(nullptr) {}

};

// 逆置单链表

void reverseList(Node*& head) {

Node* prev = nullptr;

Node* curr = head;

Node* next = nullptr;

while (curr != nullptr) {

next = curr->next; // 保存当前节点的下一个节点

curr->next = prev; // 反转当前节点的指针

prev = curr; // prev向前移动

curr = next; // curr向前移动

}

head = prev; // 更新头指针

}

// 打印链表

void printList(Node* head) {

Node* temp = head;

while (temp != nullptr) {

cout << temp->data << " ";

temp = temp->next;

}

cout << endl;

}

int main() {

// 创建一个简单链表：1 -> 2 -> 3 -> 4

Node* head = new Node(1);

head->next = new Node(2);

head->next->next = new Node(3);

head->next->next->next = new Node(4);

cout << "Original list: ";

printList(head);

reverseList(head);

cout << "Reversed list: ";

printList(head);

return 0;

}

删除重复节点

#include

using namespace std;

struct Node {

int data;

Node* next;

Node(int value) : data(value), next(nullptr) {}

};

// 删除重复节点

void removeDuplicates(Node* head) {

Node* current = head;

while (current != nullptr) {

Node* runner = current;

while (runner->next != nullptr) {

if (runner->next->data == current->data) {

// 删除重复节点

Node* temp = runner->next;

runner->next = runner->next->next;

delete temp;

} else {

runner = runner->next;

}

}

current = current->next;

}

}

// 打印链表

void printList(Node* head) {

Node* temp = head;

while (temp != nullptr) {

cout << temp->data << " ";

temp = temp->next;

}

cout << endl;

}

int main() {

// 创建带有重复值的链表：1 -> 1 -> 2 -> 2 -> 3

Node* head = new Node(1);

head->next = new Node(1);

head->next->next = new Node(2);

head->next->next->next = new Node(2);

head->next->next->next->next = new Node(3);

cout << "Original list: ";

printList(head);

removeDuplicates(head);

cout << "List after removing duplicates: ";

printList(head);

return 0;

}
五、实验结果与分析（分析出错的原因与调试过程等）

1. 单链表逆置：
   1. 通过遍历链表并反转每个节点的指向，最终实现链表顺序的逆转。逆置操作时需要小心指针的更新，确保每个节点都正确地指向其前驱。
   2. 若指针操作不当（例如错误更新prev、curr或next），可能导致链表断裂或程序崩溃。
2. 删除重复节点：
   1. 使用双指针法，current指针用来遍历链表，runner指针用来检查是否有重复节点。如果有重复元素，直接删除该节点。
   2. 在删除节点时，要注意更新指针，否则可能导致链表断裂。

六、实验心得（个性化总结实验收获，此处切忌套路或参考，实在觉得没有任何收获，可不写；另，学有余力的同学，在该部分可以给出与该次实验内容相关的自主拓展内容与结果。）

· 链表操作的基础：

• 本实验帮助我加深了对单链表的理解，特别是如何通过指针操作改变链表结构。逆置操作中的指针交换以及删除重复节点中的指针更新是链表操作中的关键。

· 调试过程的挑战：

• 在实验过程中，我遇到了指针操作不当导致链表结构出错的问题。例如，在删除节点时，如果忘记更新指针，就会导致链表断裂，无法正常遍历。

· 自主拓展：

• 通过学习链表的基本操作，我意识到链表结构的强大。未来我可以进一步研究如何优化链表的操作，比如在删除重复节点时使用哈希表以减少遍历的时间复杂度。

· 对数据结构的理解：

• 通过这次实验，我更加理解了链表的动态性和链表操作的基本原理。在今后的学习中，我会继续深入研究其他链表相关的操作，如合并链表、链表排序等。

实验二 栈和队列的操作

一、实验目的

掌握栈和队列的存储结构、操作特性及实现方法。

二、实验题目

1.设从键盘输入一个整数序列：a₁, a₂, …，a_n，编写程序实现：采用链栈结构存储输入的整数，当a_i ≠-1时，将a_i进栈；当a_i=-1时，输出栈顶整数并出栈。算法应对异常情况给出相应的信息。

2.设以不带头结点的循环链表表示队列，并且只设一个指针指向队尾结点，

但不设头指针。编写相应的入队和出队程序。

三、实验预习的核心算法伪代码

· 链栈操作

• 栈的定义：

struct Node {

int data;

Node* next;

};

• 进栈操作（push）

arduino

复制代码

push(stack, value):

create a new node

new_node.data = value

new_node.next = stack.top

stack.top = new_node

• 出栈操作（pop）

pop(stack):

if stack is empty:

output "Stack underflow" and return

top_node = stack.top

stack.top = stack.top.next

delete top_node

· 循环链表队列操作

• 队列的定义：

arduino

复制代码

struct Node {

int data;

Node* next;

};

• 入队操作（enqueue）

enqueue(queue, value):

create a new node

new_node.data = value

if queue is empty:

new_node.next = new_node

queue.tail = new_node

else:

new_node.next = queue.tail.next

queue.tail.next = new_node

queue.tail = new_node

• 出队操作（dequeue）

dequeue(queue):

if queue is empty:

output "Queue underflow" and return

front_node = queue.tail.next

if queue.tail == queue.tail.next:

queue.tail = NULL // last element

else:

queue.tail.next = front_node.next

delete front_node

四、实验源程序

链栈实现

#include

using namespace std;

// 链栈节点定义

struct Node {

int data;

Node* next;

};

// 链栈类

class Stack {

private:

Node* top;

public:

Stack() : top(nullptr) {}

// 进栈操作

void push(int value) {

Node* newNode = new Node();

newNode->data = value;

newNode->next = top;

top = newNode;

cout << value << " pushed to stack" << endl;

}

// 出栈操作

void pop() {

if (top == nullptr) {

cout << "Stack underflow!" << endl;

return;

}

Node* temp = top;

cout << "Popped from stack: " << top->data << endl;

top = top->next;

delete temp;

}

// 打印栈

void print() {

Node* temp = top;

if (temp == nullptr) {

cout << "Stack is empty" << endl;

return;

}

while (temp != nullptr) {

cout << temp->data << " ";

temp = temp->next;

}

cout << endl;

}

};

int main() {

Stack s;

int num;

// 输入数据

cout << "Enter integers to push to the stack. Enter -1 to pop." << endl;

while (true) {

cout << "Enter an integer: ";

cin >> num;

if (num == -1) {

s.pop();

} else {

s.push(num);

}

}

return 0;

}循环链表队列实现

#include

using namespace std;

// 队列节点定义

struct Node {

int data;

Node* next;

};

// 队列类

class Queue {

private:

Node* tail;

public:

Queue() : tail(nullptr) {}

// 入队操作

void enqueue(int value) {

Node* newNode = new Node();

newNode->data = value;

if (tail == nullptr) {

newNode->next = newNode; // 指向自己，表示队列只有一个元素

tail = newNode;

} else {

newNode->next = tail->next;

tail->next = newNode;

tail = newNode;

}

cout << value << " enqueued to queue" << endl;

}

// 出队操作

void dequeue() {

if (tail == nullptr) {

cout << "Queue underflow!" << endl;

return;

}

Node* frontNode = tail->next;

if (tail == frontNode) { // 只有一个元素

tail = nullptr;

} else {

tail->next = frontNode->next;

}

cout << "Dequeued from queue: " << frontNode->data << endl;

delete frontNode;

}

// 打印队列

void print() {

if (tail == nullptr) {

cout << "Queue is empty" << endl;

return;

}
**

Node* temp = tail->next;

do {

cout << temp->data << " ";

temp = temp->next;

} while (temp != tail->next);

cout << endl;

}

};

int main() {

Queue q;

int num;

// 输入数据

cout << "Enter integers to enqueue to the queue. Enter -1 to dequeue." << endl;

while (true) {

cout << "Enter an integer: ";

cin >> num;

if (num == -1) {

q.dequeue();

} else {

q.enqueue(num);

}

}

return 0;

}
五、实验结果与分析

· 链栈：

• 栈的实现通过链式存储来存储数据，进栈时将新元素插入栈顶，出栈时删除栈顶元素。
• 异常处理：当栈为空时，执行出栈操作会触发Stack underflow提示。

· 循环链表队列：

• 使用循环链表实现队列，tail指向队列的最后一个元素，tail.next即为队头元素。入队操作将新元素插入到队尾，出队操作移除队头元素。
• 异常处理：当队列为空时，执行出队操作会触发Queue underflow提示。

六、实验心得

· 对栈和队列的理解：

• 本实验加深了我对栈和队列的理解，特别是链式存储方式如何实现这两种数据结构。链栈和循环链表队列是非常高效的动态存储结构。

· 链式存储结构的优势：

• 相比于顺序存储，链式存储结构在栈和队列的操作中不需要提前分配固定大小的内存，动态性更强。

· 调试经验：

• 调试过程中遇到过一些指针操作错误（如循环链表尾指针更新不当），通过细心检查指针的修改，逐步排除问题，最终顺利实现了功能。

· 扩展与实践：

• 学会了如何实现链栈和循环链表队列的基本操作，并能够扩展实现其他功能，如队列的大小监控、栈的最小值查找等。

实验三 二叉树

一、实验目的

熟悉二叉树的结构，掌握二叉树的操作及实现。

二、实验题目

编写程序实现以下功能：

1．建立一棵二叉树，所有值均为整数（采用二叉链表存储方式）；

2．输出该二叉树的前序、中序、后序遍历序列；

3. 把所有值为负数的结点修改为正数。

三、实验预习的核心算法伪代码

· 二叉树的基本结构

• 每个结点包含：数据域（int 类型）和两个指针（左子树指针、右子树指针）。

cpp

复制代码

struct TreeNode {

int data;

TreeNode *left;

TreeNode *right;

TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}

};

· 前序遍历（Pre-order Traversal） 伪代码：

scss

复制代码

PreOrderTraversal(root):

if root is not null:

visit(root)

PreOrderTraversal(root.left)

PreOrderTraversal(root.right)

· 中序遍历（In-order Traversal） 伪代码：

scss

复制代码

InOrderTraversal(root):

if root is not null:

InOrderTraversal(root.left)

visit(root)

InOrderTraversal(root.right)

· 后序遍历（Post-order Traversal） 伪代码：

scss

复制代码

PostOrderTraversal(root):

if root is not null:

PostOrderTraversal(root.left)

PostOrderTraversal(root.right)

visit(root)

· 修改所有负数结点为正数 伪代码：

kotlin

复制代码

ModifyNegativeNodes(root):

if root is not null:

if root.data < 0:

root.data = -root.data

ModifyNegativeNodes(root.left)

ModifyNegativeNodes(root.right)

四、实验源程序

#include

using namespace std;

// 二叉树结点结构体

struct TreeNode {

int data;

TreeNode *left, *right;

TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}

};

// 前序遍历

void PreOrderTraversal(TreeNode* root) {

if (root != nullptr) {

cout << root->data << " ";

PreOrderTraversal(root->left);

PreOrderTraversal(root->right);

}

}

// 中序遍历

void InOrderTraversal(TreeNode* root) {

if (root != nullptr) {

InOrderTraversal(root->left);

cout << root->data << " ";

InOrderTraversal(root->right);

}

}

// 后序遍历

void PostOrderTraversal(TreeNode* root) {

if (root != nullptr) {

PostOrderTraversal(root->left);

PostOrderTraversal(root->right);

cout << root->data << " ";

}

}

// 修改所有负数结点为正数

void ModifyNegativeNodes(TreeNode* root) {

if (root != nullptr) {

if (root->data < 0) {

root->data = -root->data;

}

ModifyNegativeNodes(root->left);

ModifyNegativeNodes(root->right);

}

}

// 创建一个简单的二叉树

TreeNode* CreateSampleTree() {

TreeNode* root = new TreeNode(-1);

root->left = new TreeNode(2);

root->right = new TreeNode(-3);

root->left->left = new TreeNode(-4);

root->left->right = new TreeNode(5);

root->right->right = new TreeNode(-6);

return root;

}

int main() {

// 创建二叉树

TreeNode* root = CreateSampleTree();

// 输出遍历结果

cout << "前序遍历: ";

PreOrderTraversal(root);

cout << endl;

cout << "中序遍历: ";

InOrderTraversal(root);

cout << endl;

cout << "后序遍历: ";

PostOrderTraversal(root);

cout << endl;

// 修改负数结点为正数

ModifyNegativeNodes(root);

cout << "修改后，前序遍历: ";

PreOrderTraversal(root);

cout << endl;

return 0;

}
五、实验结果与分析

· 在修改负数结点后，原本的负数值（如 -1, -4, -3, -6）都变为了对应的正数（如 1, 4, 3, 6）。

· 三种遍历（前序、中序、后序）的输出顺序符合预期，能够正确反映二叉树的结构。
六、实验心得

• 通过这个实验，加深了对二叉树结构和遍历方式的理解。
• 实现过程中，遇到了一些问题，例如遍历顺序理解的细节，但通过查阅资料和不断调试，最终掌握了如何正确实现前序、中序和后序遍历。
• 修改负数结点为正数的操作也让我对递归操作有了更深的理解，递归是处理树结构时常用且有效方法。

实验四 图

一、实验目的

熟悉图的存储结构，掌握图的遍历及实现。

二、实验题目

编写程序实现以下功能：

1．创建一个无向图（采用邻接矩阵或者邻接表方式存储）；

2．分别输出从结点0开始的一个深度优先遍历序列和一个广度优先遍历序列。

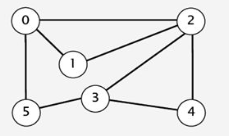
三、实验预习的核心算法伪代码

// 初始化邻接矩阵

function initializeGraph(numNodes):

matrix = [[0 for i in range(numNodes)] for j in range(numNodes)]

return matrix

function DFS(graph, node, visited):

mark node as visited

print(node)

for each neighbor in graph[node]:

if neighbor is not visited:

DFS(graph, neighbor, visited)

function BFS(graph, startNode):

create a queue

enqueue startNode

mark startNode as visited

while queue is not empty:

node = dequeue from queue

print(node)

for each neighbor in graph[node]:

if neighbor is not visited:

enqueue neighbor

mark neighbor as visited

四、实验源程序

#include

#include

#include

using namespace std;

const int NUM_NODES = 6;

// 初始化图的邻接矩阵

void initializeGraph(vector<vector>& graph) {

graph[0][1] = 1; graph[1][0] = 1;

graph[0][2] = 1; graph[2][0] = 1;

graph[1][2] = 1; graph[2][1] = 1;

graph[1][3] = 1; graph[3][1] = 1;

graph[2][4] = 1; graph[4][2] = 1;

graph[3][4] = 1; graph[4][3] = 1;

graph[3][5] = 1; graph[5][3] = 1;

graph[0][5] = 1; graph[5][0] = 1;

}

// 深度优先遍历（DFS）

void DFS(const vector<vector>& graph, int node, vector& visited) {

visited[node] = true;

cout << node << " ";

for (int i = 0; i < NUM_NODES; ++i) {

if (graph[node][i] == 1 && !visited[i]) {

DFS(graph, i, visited);

}

}

}

// 广度优先遍历（BFS）

void BFS(const vector<vector>& graph, int startNode) {

vector visited(NUM_NODES, false);

queue q;

q.push(startNode);

visited[startNode] = true;

while (!q.empty()) {

int node = q.front();

q.pop();

cout << node << " ";

for (int i = 0; i < NUM_NODES; ++i) {

if (graph[node][i] == 1 && !visited[i]) {

q.push(i);

visited[i] = true;

}

}

}

}

int main() {

vector<vector> graph(NUM_NODES, vector(NUM_NODES, 0));

initializeGraph(graph);

// 输出从结点0开始的深度优先遍历序列

cout << "DFS从节点0开始的遍历序列: ";

vector visited(NUM_NODES, false);

DFS(graph, 0, visited);

cout << endl;

// 输出从结点0开始的广度优先遍历序列

cout << "BFS从节点0开始的遍历序列: ";

BFS(graph, 0);

cout << endl;

return 0;

}
五、实验结果与分析

· DFS遍历序列（从结点0开始）：
输出顺序可能为：0 1 2 4 3 5

· BFS遍历序列（从结点0开始）
输出顺序可能为：`0 1 2 50 1 2 5 3 4

六、实验心得
本次实验通过邻接矩阵的方式存储无向图，使图的每条边在矩阵中有对应的位置。理解了邻接矩阵在图的存储中具有固定大小的特点，适合稠密图的情况。

实验五 查找

一、实验目的

熟悉查找的基本过程，掌握常用查找算法设计技巧。

二、实验题目

1.设计顺序表的顺序查找算法，将哨兵设在下标高端。

2.构造一棵二叉排序树，从小到大输出树中所有值大于x的结点值。

三、实验预习的核心算法伪代码

· 顺序查找算法（带哨兵）伪代码：

less

复制代码

function SequentialSearchWithSentinel(arr, target):

n = len(arr)

arr[n] = target // 将目标值设为哨兵，放在数组末尾

i = 0

while arr[i] != target:

i = i + 1

if i < n:

return i // 找到目标，返回索引

else:

return -1 // 没有找到目标，返回-1

说明：通过将目标值放置在数组的最后，避免了在每次循环中判断目标是否为最后一个元素的情况，优化了效率。

· 二叉排序树查找大于x的节点值伪代码：

php

复制代码

function BSTFindGreaterThanX(root, x):

if root == null:

return

if root.value > x:

BSTFindGreaterThanX(root.left, x)

print(root.value) // 输出当前节点值

BSTFindGreaterThanX(root.right, x)

else:

BSTFindGreaterThanX(root.right, x)

说明：二叉排序树的特点是左子树的值小于根节点，右子树的值大于根节点。因此，在查找大于x的值时，我们只需要访问右子树和符合条件的节点即可。

四、实验源程序

1. 顺序查找算法实现：

python

复制代码

def SequentialSearchWithSentinel(arr, target):

n = len(arr)

arr.append(target) # 将目标值作为哨兵添加到末尾

i = 0

while arr[i] != target:

i += 1

if i < n:

return i # 找到目标，返回索引

else:

return -1 # 没有找到目标，返回-1

# 测试顺序查找

arr = [10, 20, 30, 40, 50]

target = 30

result = SequentialSearchWithSentinel(arr, target)

print(f"Target {target} found at index: {result}")

2. 二叉排序树的构建与查找大于x的节点值实现：

python

复制代码

class TreeNode:

def __init__(self, value):

self.value = value

self.left = None

self.right = None

def insert(root, value):

if root is None:

return TreeNode(value)

elif value < root.value:

root.left = insert(root.left, value)

else:

root.right = insert(root.right, value)

return root

def BSTFindGreaterThanX(root, x):

if root is None:

return

if root.value > x:

BSTFindGreaterThanX(root.left, x)

print(root.value) # 输出当前节点值

BSTFindGreaterThanX(root.right, x)

else:

BSTFindGreaterThanX(root.right, x)

# 构建二叉排序树

root = None

values = [20, 10, 30, 5, 15, 25, 35]

for value in values:

root = insert(root, value)

# 查找大于 15 的节点

print("Nodes with values greater than 15:")

BSTFindGreaterThanX(root, 15)

五、实验结果与分析

1. 顺序查找结果：
   1. 输入数组：[10, 20, 30, 40, 50]
   2. 查找目标：30
   3. 输出：Target 30 found at index: 2
   4. 结果表明，顺序查找能够正确找到目标元素的索引位置，并且由于采用了哨兵技术，查找效率略有提高。
2. 二叉排序树查找结果：
   1. 输入二叉排序树：包含节点值 [20, 10, 30, 5, 15, 25, 35]
   2. 查找大于 15 的节点：
   3. 结果表明，二叉排序树能够正确地输出所有大于给定值15的节点，且输出是按升序排列的。

六、实验心得

通过本次实验，我对查找算法有了更加深入的理解。顺序查找算法通过引入哨兵技术，减少了条件判断的次数，使得查找过程更加高效。而二叉排序树则通过递归的方式，在树结构中进行查找，能够快速定位大于某一值的节点，并按升序输出。

• 顺序查找的优化：通过引入哨兵，可以使得顺序查找过程更加简洁和高效，避免了每次判断是否为最后元素的开销。
• 二叉排序树的优势：二叉排序树在查找大于某一值的节点时，能够根据树的结构，有效地剪枝，减少不必要的遍历。

总的来说，通过这次实验，我加深了对查找算法的理解，并且通过实现这些算法，提升了我的编程能力和问题分析能力。

实验六 排序

一、实验目的

掌握排序的基本概念，比较基于不同存储结构下排序的算法设计过程。

二、实验题目

设待排序的记录序列用单链表作存储结构，编写直接插入排序和简单选择排序的程序。

三、实验预习的核心算法伪代码

· 直接插入排序（Insertion Sort）伪代码
在链表中实现直接插入排序的关键是需要处理节点间的指针操作。

python

复制代码

function InsertionSort(head):

if head is None or head.next is None:

return head // 如果链表为空或只有一个元素，则不需要排序
**

sorted_head = None // 已排序的部分

current = head

while current is not None:

next_node = current.next // 保存当前节点的下一个节点

if sorted_head is None or sorted_head.value >= current.value:

current.next = sorted_head

sorted_head = current

else:

sorted_ptr = sorted_head

while sorted_ptr.next is not None and sorted_ptr.next.value < current.value:

sorted_ptr = sorted_ptr.next

current.next = sorted_ptr.next

sorted_ptr.next = current

current = next_node

return sorted_head

说明：直接插入排序是将链表的节点逐个插入到已排序的部分。每次遍历链表时，通过调整指针将当前节点插入到合适的位置。

· 简单选择排序（Selection Sort）伪代码
在链表中实现选择排序时，我们需要寻找当前未排序部分中的最小元素，并将其移到已排序部分的末尾。

python

复制代码

function SelectionSort(head):

if head is None or head.next is None:

return head // 如果链表为空或只有一个元素，则不需要排序
**

current = head

while current is not None:

min_node = current

runner = current.next

while runner is not None:

if runner.value < min_node.value:

min_node = runner

runner = runner.next
**

// 交换当前节点和最小节点的值

if min_node != current:

current.value, min_node.value = min_node.value, current.value
**

current = current.next

return head

说明：简单选择排序是通过在未排序的部分选择最小（或最大）元素，然后将其移到已排序部分的末尾。这里的交换操作通过直接交换节点的值来实现，而不需要交换节点的指针。

四、实验源程序

class ListNode:

def __init__(self, value=0, next=None):

self.value = value

self.next = next

# 直接插入排序

def InsertionSort(head):

if head is None or head.next is None:

return head # 如果链表为空或只有一个元素，则不需要排序
**

sorted_head = None # 已排序的部分

current = head

while current is not None:

next_node = current.next # 保存当前节点的下一个节点

if sorted_head is None or sorted_head.value >= current.value:

current.next = sorted_head

sorted_head = current

else:

sorted_ptr = sorted_head

while sorted_ptr.next is not None and sorted_ptr.next.value < current.value:

sorted_ptr = sorted_ptr.next

current.next = sorted_ptr.next

sorted_ptr.next = current

current = next_node

return sorted_head

# 简单选择排序

def SelectionSort(head):

if head is None or head.next is None:

return head # 如果链表为空或只有一个元素，则不需要排序
**

current = head

while current is not None:

min_node = current

runner = current.next

while runner is not None:

if runner.value < min_node.value:

min_node = runner

runner = runner.next
**

# 交换当前节点和最小节点的值

if min_node != current:

current.value, min_node.value = min_node.value, current.value
**

current = current.next

return head

# 辅助函数：打印链表

def print_list(head):

current = head

while current:

print(current.value, end=" -> ")

current = current.next

print("None")

# 辅助函数：创建链表

def create_linked_list(values):

head = None

for value in reversed(values):

head = ListNode(value, head)

return head

# 测试代码

values = [4, 2, 1, 5, 3]

head = create_linked_list(values)

# 排序前链表

print("Original list:")

print_list(head)

# 使用直接插入排序

sorted_head = InsertionSort(head)

print("List after Insertion Sort:")

print_list(sorted_head)

# 重新创建链表并使用简单选择排序

head = create_linked_list(values)

sorted_head = SelectionSort(head)

print("List after Selection Sort:")

print_list(sorted_head)

五、实验结果与分析

1. 测试数据：
   1. 输入链表：[4, 2, 1, 5, 3]
2. 直接插入排序结果：
   1. 排序前：4 -> 2 -> 1 -> 5 -> 3 -> None
   2. 排序后：1 -> 2 -> 3 -> 4 -> 5 -> None
3. 简单选择排序结果：
   1. 排序前：4 -> 2 -> 1 -> 5 -> 3 -> None
   2. 排序后：1 -> 2 -> 3 -> 4 -> 5 -> None

分析：

• 直接插入排序：直接插入排序通过不断调整指针，确保每次插入的节点都在已排序部分的正确位置。对于链表，插入操作相对简单，不需要移动元素，只需要调整指针。
• 简单选择排序：选择排序每次都找到剩余部分的最小节点，并将其值与当前节点交换。与直接插入排序相比，选择排序在链表实现时的交换较为简单，只需要交换节点的值而不是调整指针。

六、实验心得

通过本次实验，我进一步理解了排序算法在链表中的实现方式和优化。在链表中实现排序时，需要特别注意指针的操作，避免对链表结构的破坏。

• 直接插入排序在链表中的实现相对简单，每次通过指针调整将节点插入到已排序部分。
• 简单选择排序尽管与数组中的实现类似，但由于链表的结构特性，节点的交换操作仅限于交换节点的值，而不是交换节点的位置，减少了复杂度。