并查集专题
并查集专题训练
最近也是把HS找的几道史关于并查集的专题做了一遍，简单整理回顾一下
个人在洛谷题单整理的(部分题目未收录，请转到原网址）
9.11 添加了最后一题
并查集基础模板 cogs259 亲戚 P3367 模板并查集
我可以只讲思路，不讲代码吗
——致敬传奇讲课王HS
题目大意
有n个元素和m次操作，每次操作分别为
- 把x , y合并到一个集合
- 查询x , y是否在一个集合
对于这个问题，可以使用并查集解决
并查集概念
并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素
浅显一点就是把不同的元素放入一个容器，小容器可以再放入大容器
对于容器，我们有两种操作
- 合并（Union）：合并两个元素所属集合（合并对应的树/容器）
- 查询（Find）：查询某个元素所属集合（查询对应的树的根节点/大容器），这可以用于判断两个元素是否属于同一集合
对于任意一个元素ai所属的集合，可以定义为 f[ai]，最初ai所属集合为自己，则可以实现合并与查询操作
查询x所属集合
int find(int x){
if(f[x]==x)
return x;
return find(x);
}
//利用递归算法寻找根节点，根节点所属集合一定为自身
把x与y合并到一个集合
void Union(int x,int y){
f[y]=x;//y的所属集合加入x
}
如果这么查找任意一个点所属集合的话复杂度到达了O(n)级别，显然十分鸡肋，所以我们引入一个优化方法，路径压缩
这是集合的初始形态
这是压缩后的
显然，如果只是查询所在集合，对于
f[x]只需指向最高根节点就行，所以有了路径优化算法
int find(int x){
if(f[x]==x)
return x;
return f[x]=find(f[x]);
}
//查找过程中把最后的根节点赋值给路径上所有点
合并算法也同理
void join(int x,int y){
int rx=find(x),ry=find(y);
f[ry]=rx;
}
//把y所在集合根节点连接x所在根节点
对于压缩路径，复杂度不会大于O(logn)
代码
这里粘贴的是洛谷的P3367上的代码，仅供并查集具体查询合并的参考
ps：注意附上链接的两题输入输出略有差异
#include<bits/stdc++.h>
using namespace std;
int n,m,q,f[100010];
int fi(int x){//查询
if(f[x]==x)
return x;
return f[x]=fi(f[x]);
}
void hb(int x,int y){//合并
int u=fi(x),v=fi(y);
if(u==v){
return;
}
f[v]=u;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
f[i]=i;
for(int i=1;i<=m;i++){
int x,y,z;
cin>>z>>x>>y;
if(z==1)//判断查询与合并
hb(x,y);
else{
if(fi(x)==fi(y)){
cout<<"Y"<<endl;
}
else{
cout<<"N"<<endl;
}
}
}
return 0;
}
基础并查集应用
[NOI2015] 程序自动分析 【logu】[NOI2015] 程序自动分析 【cogs】[NOI2015] 程序自动分析
题目大意
有n个元素，每次给定其中元素x与y，有两种判定，一种是x=y，一种是x!=y，经过m次判断后判断是否有冲突判定，无输出“Yes”，有则输出"No"
例：若x=y , y=z , 则x!=z是冲突的
思路
很朴实的一道并查集板子题，若x=y则把x与y加入一个集合，最后再判断每次不等于判断的二者是否在同一集合，如果判定为真则直接输出no
注意，这道题的ai大小为109，直接`f[ai]`超过了内存限制无法存下。但元素只有105，可以离散化存储
代码
#include<bits/stdc++.h>
using namespace std;
int t,n,fa[300010];
vector<long long>v;
struct node{
int x;
int y;
int z;
}e[100010];
int get(int x){
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
//离散化中二分求下标
int find(int x,int l){
if(fa[x]==x){
return x;
}
return fa[x]=find(fa[x],x);
}
void join(int x,int y){
int rx=find(x,0),ry=find(y,0);
if(rx==ry)
return;
fa[ry]=rx;
}
int ask(int x,int y){
int rx=find(x,0),ry=find(y,0);
if(rx==ry)
return 1;
return 0;
}
int main(){
cin>>t;
while(t--){
cin>>n;
v.clear();
for(int i=1;i<=n;i++){
cin>>e[i].x>>e[i].y>>e[i].z;
v.push_back(e[i].x);
v.push_back(e[i].y);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
//离散化
for(int i=1;i<=n;i++){
e[i].x=get(e[i].x);
e[i].y=get(e[i].y);
fa[e[i].x]=e[i].x;
fa[e[i].y]=e[i].y;
}
for(int i=1;i<=n;i++){
if(e[i].z==0)
continue;
join(e[i].x,e[i].y);
}
for(int i=1;i<=n;i++){
if(e[i].z==0){
if(ask(e[i].x,e[i].y)==1){
cout<<"NO"<<endl;
break;
}
}
if(i==n){
cout<<"YES"<<endl;
}
}
}
return 0;
}
带权并查集
概念
在并查集的基础上加上权值扩展，解决更多的问题
银河英雄传说【luogu】银河英雄传说【cogs】银河英雄传说
个人找了一篇认为讲解带权并查集不错的题解（因为我懒得再写一次这题）
动物园 【cogs】动物园
接下来是这个题单的带权并查集扩展三部曲，前两题是第三题的前置，有一定的思维难度
这道我认为是带权并查集很好的练习题，很可惜没有在洛谷上找到相似题拿双倍经验
题目大意
对于任意两点 p 和 q，f(p,q) 是 p 到 q 所有简单路径中，经过路径权值的最小值
题目要求计算所有点对 (p,q)（其中
p!=q）的 f(p,q) 的总和
思路
题目看起来还是很裸的，如果两个子树依靠第i条路径联通且i为其中最小值，只需要把ans加上两子树所构成的数对个数乘以i即可，难点就在于两点的路径不唯一，后添加的路径可能会构成更优的方案
仔细思考一下，其实这道题就是取k条路径让所有节点联通，同时每一条的边权都尽可能的大(类似于最小生成树)，所以我们可以把边以边权从大到小排序以此合并每个q，p集合中最大边权，解决掉后效性问题
代码
#include<bits/stdc++.h>
using namespace std;
long long n,m,q,f[100010],a[100010],k[100010],ans;
struct node{
long long x;
long long y;
long long z;
}e[1000010];
long long cmp(node A,node B){
if(A.z==B.z)
return A.x<B.x;
return A.z>B.z;
}
long long fi(long long x){
if(f[x]==x){
return x;
}
return f[x]=fi(f[x]);
}
void hb(long long x,long long y,long long z){
long long u=fi(x),v=fi(y);
if(u==v){
return;
}
ans+=(k[u]*k[v])*z*2;
k[u]+=k[v];
f[f[y]]=f[u];
}
int main(){
freopen("happyzoo.in","r",stdin);
freopen("happyzoo.out","w",stdout);
cin>>n>>m;
for(long long i=1;i<=n;i++){
f[i]=i;
cin>>a[i];
k[i]=1;
}
for(long long i=1;i<=m;i++){
cin>>e[i].x>>e[i].y;
if(e[i].y<e[i].x)
swap(e[i].x,e[i].y);
e[i].z=min(a[e[i].x],a[e[i].y]);
}
sort(e+1,e+m+1,cmp);
for(long long i=1;i<=m;i++){
hb(e[i].x,e[i].y,e[i].z);
}
cout<<ans;
return 0;
}
ps：这道题我在已知思路的情况下调了两个小时，原因是把并查集中f[rooty]=rx写成了f[y]=rx,样例离谱的过了
可见我抽象的编码能力和查找问题的能力有多垃圾
食物链 【luogu】食物链【cogs】食物链
题目大意
有3种动物互相克制，现在每次给一组x，y表示x被y克制或x与y是同类，但如果与之前给出的有冲突，就是假话，即
- 当前的话与前面的某些真的话冲突，就是假话
- 当前的话中X或Y比N大，就是假话
- 当前的话表示X吃X，就是假话
输出假话的数量
思路
这道题牵扯到了并查集的一个种类问题，也就是题目给定了集合数量，把元素按照最优解分配到各个集合里面，各个集合之间都有传递性
我们只需要把x克制的设置为x+n，天敌为x+2*n，所以我们需要在每次合并时把两个x，y的三种元素合并，即
- 当x,y为同类，把x+n，y+n以及x+2*n，y+2*n全部合并
- 当x吃y，则x与y+2n合并，x+n与y合并，x+2*n与y+n合并
代码
#include<bits/stdc++.h>
using namespace std;
int n,k,ans,fa[1000010];
inline int read()
{
int sum=0;
char ch=getchar();
while(ch>'9'||ch<'0') ch=getchar();
while(ch>='0'&&ch<='9') sum=sum*10+ch-48,ch=getchar();
return sum;
}
int find(int x){
if(fa[x]==x)
return x;
return fa[x]=find(fa[x]);
}
void join(int x,int y){
int rx=find(x),ry=find(y);
fa[ry]=rx;
}
int main(){
cin>>n>>k;
for(int i=1;i<=3*n;i++)
fa[i]=i;
for(int i=1;i<=k;i++){
int d,x,y;
d=read(),x=read(),y=read();
if(max(x,y)>n){
ans++;
continue;
}
if(d==1){
if(find(y)==find(x+n)||find(y)==find(x+2*n)){
ans++;
continue;
}
join(x,y),join(x+n,y+n),join(x+2*n,y+2*n);
}
else{
if(x==y){
ans++;
continue;
}
if(find(x)==find(y)||find(y)==find(x+2*n)){
ans++;
continue;
}
join(x,y+2*n),join(x+n,y),join(x+2*n,y+n);
}
}
cout<<ans;
return 0;
}
关押罪犯 【cogs】关押罪犯 【luogu】关押罪犯
引入
这道题个人认为难度可以到达省选-，不过远古题自动减难度
题目大意
给定两个集合，把n个数a1...an分配放入，有m对数之间有权值，若两数放入一个集合就会生效。最终权值为生效的最大权值，求如何让最终权值最小
思路
之前的两道题可以说是这道题的前置了。根据前面的思路，把每对数权值按从大到小排序，但不同的是尽量不选前面的数对。对于一组x，y，如果x的最大敌人与y的最大敌人已经在同一集合才不得不选此数对
- 设x+n为x的敌人，每次双方若不在一集合则把x+n，y加入一个集合
- ans的值即为每次x，y合并是的权值最大值（准确来说是第一次合并，应该可以优化）
代码
#include<bits/stdc++.h>
using namespace std;
int n,k,fa[40010],m,ans;
inline int read()
{
int sum=0;
char ch=getchar();
while(ch>'9'||ch<'0') ch=getchar();
while(ch>='0'&&ch<='9') sum=sum*10+ch-48,ch=getchar();
return sum;
}
struct node{
int x;
int y;
int z;
}e[100010];
bool cmp(node A,node B){
return A.z>B.z;
}
int find(int x){
if(fa[x]==x)
return x;
return fa[x]=find(fa[x]);
}
void join(int x,int y){
int rx=find(x),ry=find(y);
fa[ry]=rx;
}
int main(){
cin>>n>>m;
for(int i=1;i<=2*n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
cin>>e[i].x>>e[i].y>>e[i].z;
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++){
int x=e[i].x,y=e[i].y,z=e[i].z;
if(find(x+n)!=find(y+n)){
join(x+n,y);
join(x,y+n);
}
else{
join(x,y);
join(x+n,y+n);
ans=max(ans,z);
}
}
cout<<ans;
return 0;
}
并查集其他应用
树 【luogu】树【cogs】树
直接开讲
后三题前的幽默蓝题之耻了，没什么好讲的，每次打标记再找最深深度就行了，普通并查集就能过
不是一条路径查询问题 【cogs】不是一条路径查询问题
又是一道写过忘了正解的题，时间有限先挖坑
呜呜呜 【cogs】呜呜呜
题目大意
byd的这题怎么描述
思路
还是经典把每个c排个降序，这样的话保证每次把ci插入的c都是最小值直接使用，再用并查集维护当前所在连续区间内的ai，bi最大值
铭记
因为这道题我先看题了没有听正解，所以线段树加快读卡常，大家看个乐子
#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
struct abc{
long long x;
long long y;
}c[1000010];
inline int read()
{
int k=0,f=1;
char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) k=(k<<1)+(k<<3)+(c&15);
return k*f;
}
long long l1[1000010],r1[1000010],al,ar,a[1000010],b[1000010],sa[4000010],sb[4000010],n,ans;
long long fl(long long x){
if(l1[x-1])
return l1[x]=fl(l1[x-1]);
return x;
}
long long fr(long long x){
if(r1[x+1])
return r1[x]=fr(r1[x+1]);
return x;
}
void tj(long long x){
l1[x]=x;
r1[x]=x;
if(l1[x-1])
l1[x]=fl(x-1);
if(r1[x+1])
r1[x]=fr(x+1);
}
void js1(long long k,long long l,long long r){
if(l==r){
sa[k]=a[l];
return;
}
js1(k*2,l,(l+r)/2);
js1(k*2+1,(l+r)/2+1,r);
sa[k]=max(sa[k*2],sa[k*2+1]);
}
void js2(long long k,long long l,long long r){
if(l==r){
sb[k]=b[l];
return;
}
js2(k*2,l,(l+r)/2);
js2(k*2+1,(l+r)/2+1,r);
sb[k]=max(sb[k*2],sb[k*2+1]);
}
void ask1(long long k,long long l,long long r,long long x,long long y){
if(l>y||r<x)
return;
if(x<=l&&y>=r){
al=max(sa[k],al);
return;
}
ask1(k*2,l,(l+r)/2,x,y);
ask1(k*2+1,(l+r)/2+1,r,x,y);
}
void ask2(long long k,long long l,long long r,long long x,long long y){
if(l>y||r<x)
return;
if(x<=l&&y>=r){
ar=max(sb[k],ar);
return;
}
ask2(k*2,l,(l+r)/2,x,y);
ask2(k*2+1,(l+r)/2+1,r,x,y);
}
long long cmp(abc A,abc B){
return A.x>B.x;
}
int main(){
cin>>n;
for(long long i=1;i<=n;i++)
a[i]=read();
for(long long i=1;i<=n;i++)
b[i]=read();
for(long long i=1;i<=n;i++){
c[i].x=read();
c[i].y=i;
}
sort(c+1,c+n+1,cmp);
js1(1,1,n);
js2(1,1,n);
for(long long i=1;i<=n;i++){
long long z=c[i].y;
tj(z);
long long x=fl(z),y=fr(z);
al=0;
ar=0;
ask1(1,1,n,x,c[i].y);ask2(1,1,n,c[i].y,y); ans=max(ans,ar*al*c[i].x);
}
cout<<ans;
return 0;
}
[USACO18OPEN]Disruption P
【luogu】Disruption P【cogs】Disruption
终于到了最后一题，这道题有一个显然的树剖板子，但不得不说第一个想到并查集求路径维护的真是一个甜菜
题目大意
给一个树以及m条边，每条边带一个边权，求对于任意条边删除后想要维护图的联通性需要添加的边权最小的边
思路
首先这道题一眼丁真，明显可以枚举每一条路径两条树剖求线段树最小值来做，复杂度大概是 $ O(nlog2n) $
但事实上树剖求点找了许多无用的路径，可以就行优化
- 首先，对于任意一条可添(u,v)边来说，他们所能影响到的值就是(u,v)两点间在树上经过的所有路径
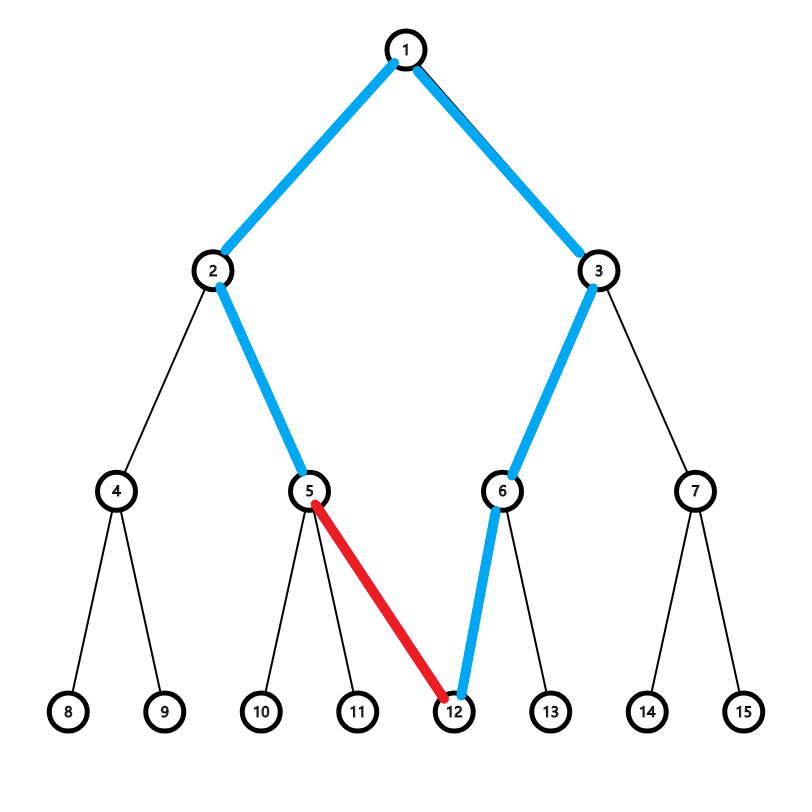如图，（u，v）更新只会影响到所在树上路径 - 我们对于每条边进行排序再遍历，则每次树上未赋值的路径最优解即为当前所枚举的（u,v)
- 显然，我们可以用lca来求出（u，v）路径，同时每一条赋值过的路径用并查集压缩避免再次判断
这道题大体思路想出来后就要感叹紫题智齿了，不过如果没有并查集标签和知道题目考察所在的并查集应用类型怕是这辈子想不出来
代码
for(int i=1;i<=m;i++){
int x=find(e[i].x),y=find(e[i].y);
int zx=lca(x,y);
while(d[x]>d[zx]){
v1[make_pair(p[x][0],x)]=e[i].z;
v1[make_pair(x,p[x][0])]=e[i].z;
f[x]=find(p[x][0]);
x=find(x);
}
while(d[y]>d[zx]){
v1[make_pair(p[y][0],y)]=e[i].z;
v1[make_pair(y,p[y][0])]=e[i].z;
f[y]=find(p[y][0]);
y=find(y);
}
}
for(int i=1;i<=n-1;i++){
if(v1[make_pair(lj[i][0],lj[i][1])]==0)
cout<<"-1"<<endl;
else
cout<<v1[make_pair(lj[i][0],lj[i][1])]<<endl;
}
核心代码还是展示一下
铭记
p[100010][21]
我开成了
p[100010][20]
结果部分数据数组越界，但是大部分数据都过了，又调了2h，动物园经典复刻
