平衡树
之前不是怎么会所以就从头说
1.定义,性质:
平衡树大概是二叉搜索树与堆合并形成的一种数据结构(tree + heap = treap)
需要注意的是,由于二叉搜索树与堆的性质有点矛盾(二叉:left < root <rignt 堆:root < left and rignt)所以就有了平衡术中不能以单一的键值作为节点的val
对于treap上的每一个节点都有两个值(val,id):
val:满足二叉搜索树的性质。
key
:随机生成,满足堆的性质,即优先级
2.无旋treap:
Tree{
int l,r;
int val ;
int size ;
int id ;
}
Creat a new dot:
int build(int val){
tree[++tot].val = v..al ;
tree[tot].id = rand() ;
tree[tot].l = tree[tot].r = 0 ;
tree[tot].size = 1 ;
return tot ;
}
void pushup(int x)
{
tree[x].size = tree[tree[x].l].size + tree[tree[x].r].size+1;
}
分裂split:(k,val,x,y)
把以k为root的子树按照权值val分裂:
1.val1(son) < val(root) 分到以x为根的子树
2.val2(son) > val(root) 分到以y为根的子树
具体的呢我直接饮用:
如果这个节点的权值是小于等于 val 的,说明节点 k 和节点 k 的左子树都会被划分到子树 x 上去,而 k 的右子树还没有被划分,那我们就需要再递归一下去划分 k 的右子树。注意此处我们是带引用的在进行递归,所以如果有要划分到 x 上的节点,直接把他挂上去即可。
void split(int k,int val,int &x,int &y)
{
if(!k)//root没了
{
x = y = 0 ;
return ;
}
// 看似像是递归
if(tree[k].val <= val )
{
x = k ;
split(tree[k].r,val,tree[k].r,y) ;
}
else
{
y = k ;
split(tree[k].l,val,x,tree[k].l) ;
}
push_up(k) ;
}
合并merge:
将以 x 为根的子树与以 y 为根的子树合并,需要注意的是我们这里保证了以 x 为根的子树的权值最大值小于以 y 为根的子树的权值最小值。同时我们需要不断维护优先级,因为有如上的性质,所以我们不用判断节点权值的大小而可以直接进行合并,最后这段代码返回的值是合并完两棵子树后的根节点。
int merge(int x,int y)
{
if(!x || !y) return x + y ;
if(tree[x].id >tree[y].id)
{
tree[x].r = merge(tree[x].r,y) ;
push_up(x) ;
return x ;
}
//根据对称性
else {
tree[x].l = merge(x,tree[y].l) ;
push_up(y) ;
return y ;
}
}
nexmoe
然后就是维护id:
如果 x 的优先级大于 y 的优先级,那么 x 和它的左子树我们就不需要动,需要处理的是 x 的右子树和 y
的合并问题,递归处理即可。
反之,y的优先级大于 x 的优先级亦同。理,我们仍然可以递归处理 y 的左子树和 x
按照这个过程一直递归,当有一棵子树为空,则返回 x+y
3.还有一些操作:
插入:
向平衡树中插入一个权值为 val的节点。
实现时,按照权值 val−1
进行分裂,分裂后,权值小于 val−1 的节点都在 x 子树中,其它节点在 y 子树中,先把 x 和新建的节点合并,再合并整棵树。
void insert(int val)
{
int x ;
int y ;
split(root,val-1,x,y);
root = merge(merge(x,build(val)),y) ;
}.
删除:
分裂之后,以 y 为根的子树里只有权值等于 val的节点,合并左右子树,并删除根即可。删除完成后,将整棵树重新合并。
void del(int val)
{
int x,y,z;
split(root,val,x,z);
split(x,val-1,x,y);
if(y) y = merge(tree[y].l,tree[y].r) ;
root = merge(merge(x,y),z) ;
}
查询排名:
x的排名:比x小的数的个数cnt+1分裂之后插x子树size大小
int getrk(int val)
{
int x,y,ans;
split(root,val-1,x,y) ;
ans = tree[x].size - 1 ;
root = merge(x,y) ;
return ans ;
}
查询排名为k的数:
int getval(int rk)
{
int k = root ;
while(k)
{
if(tr[tr[k].l].siz+1==rank) break;
else if(tr[tr[k].l].siz>=rank) k=tr[k].l;
else rank-=tr[tr[k].l].siz+1,k=tr[k].r;
}
return !k : INF : tree[k].val ;
}
查找前驱与后继:
int getpre(int val)
{
int x,y,k,ans;
split(root,val-1,x,y);//把整棵树分裂,然后每次分裂取x子树中最靠右的节点
k=x;
while(tr[k].r) k=tr[k].r;
ans=tr[k].val;
root=merge(x,y);
return ans;
}
int getnext(int val)
{
int x,y,k,ans;
split(root,val,x,y);
k=y;
while(tr[k].l) k=tr[k].l;
ans=tr[k].val;
root=merge(x,y);
return ans;
}
最后sui手敲一个模板吧:
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,INF=1e9;
inline int read()
{
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') { if(ch=='-') w*=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
int n;
struct node{ int l,r,val,siz,key; }tr[N];
inline int random(int lim) { return rand()*rand()%lim+1; }
struct Treap{//封装Treap
int tot,root;
inline void pushup(int k) { tr[k].siz=tr[tr[k].l].siz+tr[tr[k].r].siz+1; }
inline int build(int val){
tr[++tot].val=val,tr[tot].key=random(INF);
tr[tot].l=tr[tot].r=0,tr[tot].siz=1;
return tot;
},,
inline void split(int k,int val,int &x,int &y){
if(!k) { x=y=0; return; }
if(tr[k].val<=val) x=k,split(tr[k].r,val,tr[k].r,y);
else y=k,split(tr[k].l,val,x,tr[k].l);
pushup(k);
}
inline int merge(int x,int y){
if(!x||!y) return x+y;。
if(tr[x].key>tr[y].key){
tr[x].r=merge(tr[x].r,y),pushup(x);
return x;
}
else{
tr[y].l=merge(x,tr[y].l),pushup(y);
return y;
}
}
inline void insert(int val){
int x,y;
split(root,val-1,x,y);
root=merge(merge(x,build(val)),y);
}
inline void delet(int val){
int x,y,z;
split(root,val,x,z),split(x,val-1,x,y);
if(y) y=me。。rge(tr[y].l,tr[y].r);
root=merge(merge(x,y),z);
}
inline int getrank(int val){
int x,y,ans;
split(root,val-1,x,y);
ans=tr[x].siz+1,root=merge(x,y);
return ans;
}
inline int getval(int rank){
int k=root;
while(k){
if(tr[tr[k].l].siz+1==rank) break;
else if(tr[tr[k].l].siz>=rank) k=tr[k].l;
else rank-=tr[tr[k].l].siz+1,k=tr[k].r;
}
return !k?INF:tr[k].val;
}
inline int getpre(int val){
int x,y,k,ans;
split(root,val-1,x,y),k=x;
while(tr[k].r) k=tr[k].r;
ans=tr[k].val,root=merge(x,y);
return ans;
}
inline int getnext(int val){
int x,y,k,ans;
split(root,val,x,y),k=y;
while(tr[k].l) k=tr[k].l;
ans=tr[k].val,root=merge(x,y);
return ans;
}
}treap;
int main()
{
n=read();
for(register int i=1;i<=n;i++){
int opt=read(),x=read();
if(opt==1) treap.insert(x);
else if(opt==2) treap.delet(x);
else 。。if(opt==3) printf("%d\n",treap.getrank(x));
else if(opt==4) printf("%d\n",treap.getval(x));
else if(opt==5) printf("%d\n",treap.getpre(x));
else if(opt==6) printf("%d\n",treap.getnext(x));
}
return 0;
}
嗨嗨嗨,splay来喽:
就是一种通过旋转来维护的Treap
前置LCT:实边和虚边用到了一些LCT的性质
之前最不理解的是Splay的旋转:
首先来说你这个旋转有一些东西是不能改变的:
1.整棵 Splay 的中序遍历不变
2.受影响的节点维护的信息依然正确有效。
3.root 必须指向旋转后的根节点。
举个栗子:
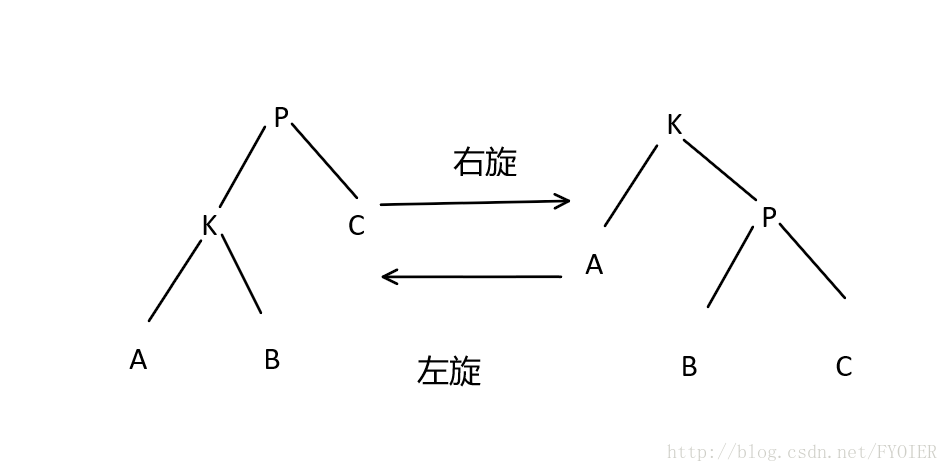
我们现在要把x节点旋转对吧,y为x节点的父亲节点:
1.将y的左儿子指向x的右儿子,且x的右儿子(如果x有右儿子的话)的父亲指向y;
ch[y][0]=ch[x][1];
fa[ch[x][1]]=y;
2.将x的右儿子指向y,且y的父亲指向x;
ch[x][chk^1]=y;
fa[y]=x;
3.如果原来的y还有父亲z,那么把z的某个儿子(原来y所在的儿子位置)指向x,且x的父亲指向z.
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
写出来就是above
void rotata(int x)
{
int y = fa[x] ;
int z = fa[y] ;
int k = get(x) ; //判断x是y的左或者右儿子
ch[y][k] = ch[x][k^1] ;
ch[x][k^1] = y ;
fa[y] = x ;
fa[x] = z ;
fa[ch[y][k]] = y ;
if(z)
{
ch[z][ch[z][1] == y] = x ;
}
maintain(y);
maintain(x);
}
偷来一张图看一看

Splay操作呢
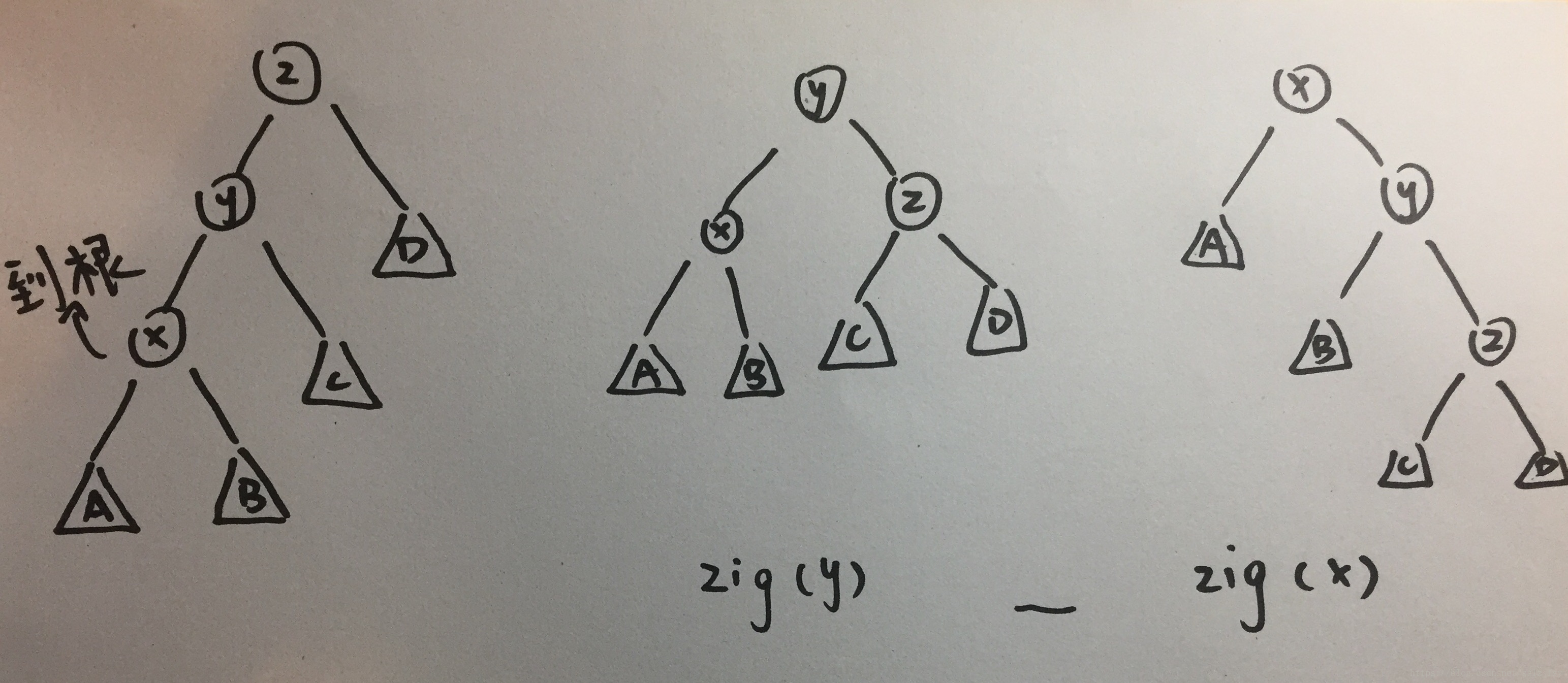
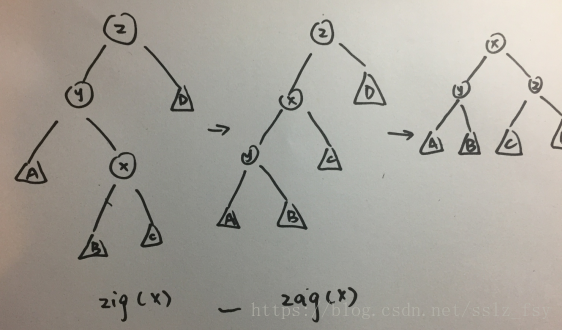
zig,zig-zig,zig-zag
zig:当目标节点是根节点的左子节点或右子节点时,进行一次单旋转,将目标节点调整到根节点的位置
zig-zig:x是它爸的什么儿子,它爸就是它爷爷的什么儿子(它们的线是直的)
zig-zag:x是它爸什么儿子,它爸就不是它爷爷什么儿子(它们是弯的)
struct node{
int fa ;
int val ;
int size ;//子树大小
int cnt ;//与该dot权值相同的点的个数
}tree[MAXN];
int son[MAXN][2] ;//i,0:i点左儿子,1-右儿子
void push_up(int k)
{
tree[k].size = tree[k].cnt + tree[son[k][0]].size + tree[son[k][1]].size;
}
void rotata(int x)
{
int y = fa[x] ;
int z = fa[y] ;
int k = get(x) ; //判断x是y的左或者右儿子
ch[y][k] = ch[x][k^1] ;
ch[x][k^1] = y ;
fa[y] = x ;
fa[x] = z ;
fa[ch[y][k]] = y ;
if(z)
{
ch[z][ch[z][1] == y] = x ;
}
maintain(y);
maintain(x);
}
void splay(int x) {
for (int f = fa[x]; f = fa[x], f; rotate(x))
if (fa[f]) rotate(get(x) == get(f) ? f : x);
rt = x;
}
#include<bits/stdc++.h>
#define ls(x) T[x].ch[0]
#define rs(x) T[x].ch[1]
#define fa(x) T[x].fa
#define root T[0].ch[1]
using namespace std;
const int MAXN=1e5+10,mod=10007,INF=1e9+10;
inline char nc()
{
static char buf[MAXN],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin)),p1==p2?EOF:*p1++;
}
inline int read()
{
char c=nc();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=nc();}
return x*f;...
}
struct node
{
int fa,ch[2],val,rec,sum;
}T[MAXN];
int tot=0,pointnum=0;
void update(int x){T[x].sum=T[ls(x)].sum+T[rs(x)].sum+T[x].rec;}
int ident(int x){return T[fa(x)].ch[0]==x?0:1;}
void connect(int x,int fa,int how){T[fa].ch[how]=x;T[x].fa=fa;}
void rotate(int x)
{
int Y=fa(x),R=fa(Y);
int Yson=ident(x),Rson=ident(Y);
connect(T[x].ch[Yson^1],Y,Yson);
connect(Y,x,Yson^1);
connect(x,R,Rson);
update(Y);update(x);
}
void splay(int x,int to)
{
to=fa(to);
while(fa(x)!=to)
{
int y=fa(x);
if(T[y].fa==to) rotate(x);
else if(ident(x)==ident(y)) rotate(y),rotate(x);
else rotate(x),rotate(x);
}
}
int newnode(int v,int f)
{
T[++tot].fa=f;
T[tot].rec=T[tot].sum=1;
T[tot].val=v;
return tot;
}
void Insert(int x)
{
int now=root;
if(root==0) {newnode(x,0);root=tot;}//
else
{
while(1)
{
T[now].sum++;
if(T[now].val==x) {T[now].rec++;splay(now,root);return ;}
int nxt=x<T[now].val?0:1;
if(!T[now].ch[nxt])
{
int p=newnode(x,now);
T[now].ch[nxt]=p;
splay(p,root);return ;
}
now=T[now].ch[nxt];
}
}
}
int find(int x)
{
int now=root;
while(1)
{
if(!now) return 0;
if(T[now].val==x) {splay(now,root);return now;}
int nxt=x<T[now].val?0:1;
now=T[now].ch[nxt];
}
}
void delet(int x)
{
int pos=find(x);
if(!pos) return ;
if(T[pos].rec>1) {T[pos].rec--,T[pos].sum--;return ;}
else
{
if(!T[pos].ch[0]&&!T[pos].ch[1]) {root=0;return ;}
else if(!T[pos].ch[0]) {root=T[pos].ch[1];T[root].fa=0;return ;}
else
{
int left=T[pos].ch[0];
while(T[left].ch[1]) left=T[left].ch[1];
splay(left,T[pos].ch[0]);
connect(T[pos].ch[1],left,1);
connect(left,0,1);//
update(left);
}
}
}
int rak(int x)
{
int now=root,ans=0;
while(1)
{
if(T[now].val==x) return ans+T[T[now].ch[0]].sum+1;
int nxt=x<T[now].val?0:1;
if(nxt==1) ans=ans+T[T[now].ch[0]].sum+T[now].rec;
now=T[now].ch[nxt];
}
}
int kth(int x)//排名为x的数
{
int now=root;
while(1)
{
int used=T[now].sum-T[T[now].ch[1]].sum;
if(T[T[now].ch[0]].sum<x&&x<=used) {splay(now,root);return T[now].val;}
if(x<used) now=T[now].ch[0];
else now=T[now].ch[1],x-=used;
}
}
int lower(int x)
{
int now=root,ans=-INF;
while(now)
{
if(T[now].val<x) ans=max(ans,T[now].val);
int nxt=x<=T[now].val?0:1;//这里需要特别注意
now=T[now].ch[nxt];
}
return ans;
}
int upper(int x)
{
int now=root,ans=INF;
while(now)
{
if(T[now].val>x) ans=min(ans,T[now].val);
int nxt=x<T[now].val?0:1;
now=T[now].ch[nxt];
}
return ans;
}
int main()
{
#ifdef WIN32
freopen("a.in","r",stdin);
#else
#endif
int N=read();
while(N--)
{
int opt=read(),x=read();
if(opt==1) Insert(x);
else if(opt==2) delet(x);
else if(opt==3) printf("%d\n",rak(x));
else if(opt==4) printf("%d\n",kth(x));
else if(opt==5) printf("%d\n",lower(x));
else if(opt==6) printf("%d\n",upper(x));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号