<轻量算法>根据核密度估计检测波峰算法 ---基于有限状态自动机和递归实现

原创博客，转载请联系博主！

 

希望我思考问题的思路，也可以给大家一些启发或者反思！

 

问题背景：

　　现在我们的手上有一组没有明确规律，但是分布有明显聚簇现象的样本点，如下图所示：　　

 

　　　

　　　　　　　　　　

 

 

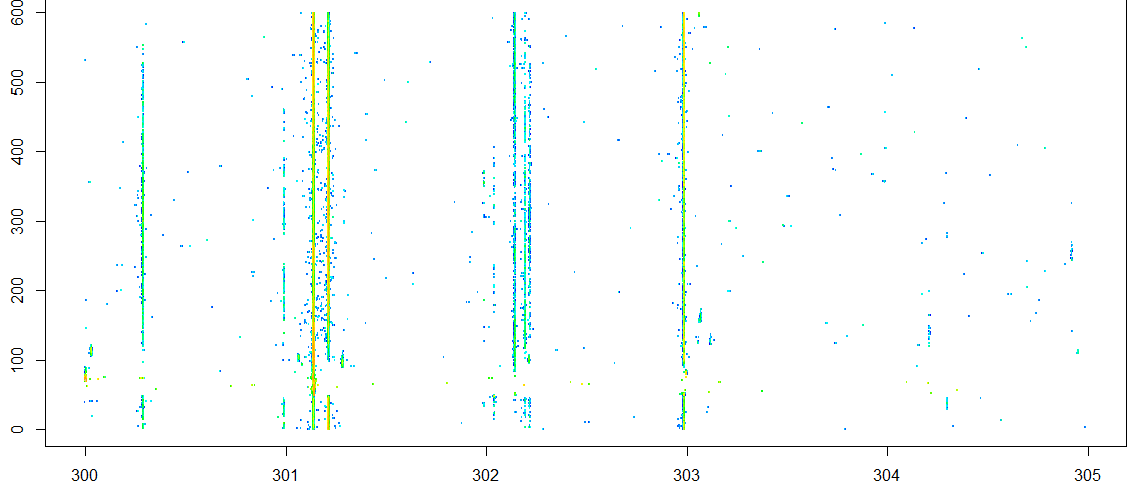
　　图中数据集是显然是个3维的数据集，包括横纵坐标和色彩（高度），由于数据的分布比较不均匀，我们选择分布比较典型的[300，305)区间的数据点进行处理

　　

　　我们的目的是找出这个数据空间中数据比较集中的部分，根据肉眼对样本的初步观察，这篇文章将讨论一个从横轴的维度对数据较密集的区域进行识别的一个轻量算法，其实也就是找出数据空间中的所谓“条状物”。 

 

算法思路：

 

　　其实如果不限制处理数据的维度，那么一个更准确的算法思路是使用非圆形聚类算法对数据样本进行处理，经过实验结果也确实符合我们的想法。

 

　　在这里我们的思路是这样的：

 

　　1.首先使用核密度估计算法对样本区间进行一个直观的统计

　　2.对样本进行归一化

　　3.对处理后的样本做求导数（这里为了追求效率使用向后差分）

　　4.通过对样本的统计结果使用有限状态自动机进行扫描，得到一个记录的峰值的结果

 

　　这里为了客观衡量算法的效率和准确度我们使用一个 加速比 和 过滤比 作为标准。

 

　　过滤比：  =得到的“条状物”中的样本的个数/样本的全部个数

　　

　　加速比：  =得到的“条状物”的横轴长度/整个样本横轴区间长度

 

　　

 

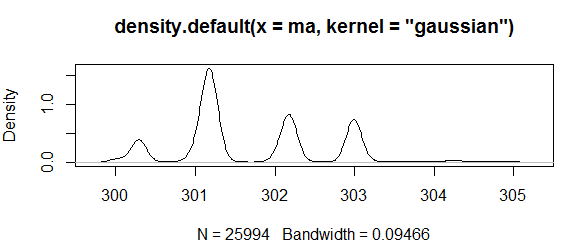
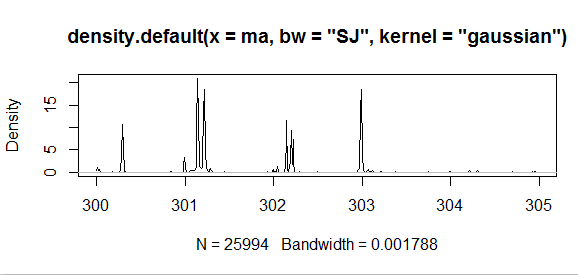
　　由于核密度估计的核函数有很多种选择，包括高斯核，伽马核，三角核，矩形核等，我们这里选择相对比较平滑的高斯核核函数对样本进行核密度估计统计，而且带宽的选择也有两种一个是迭代计算的，结果拟合得比较真实准确但是速度比较慢，另一种是非迭代计算的，计算速度很快但是结果也过于“平滑”。如下图所示：

　　非迭代计算核密度估计：

　　

 

 

　　迭代计算核密度估计：

　　

 

 

　　时间消耗对比也非常明显：

　　

　　

 

　　所以我们处理的策略是： 用非迭代的核密度估计处理大区间的数据，当区间的长度小于一个阈值的时候，使用迭代的核密度估计对数据进行准确的拟合。

 

　　梳理下来总的思路可以用下图来表示：

 

　　1.对过大的区间进行等分成“足够小”的大区间

 

 

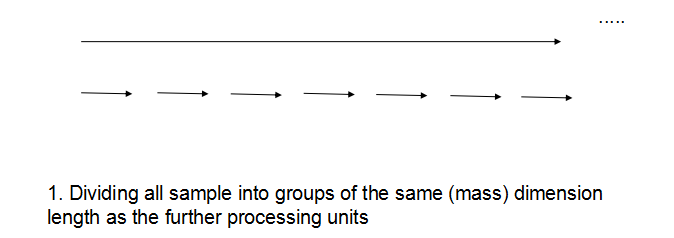
　　2.对分割后的区间进行递归的“统计+寻峰” （一个普通的递归处理，将起点放入peakStart数组中，终点放入peakEnd数组中）

 

　　

 

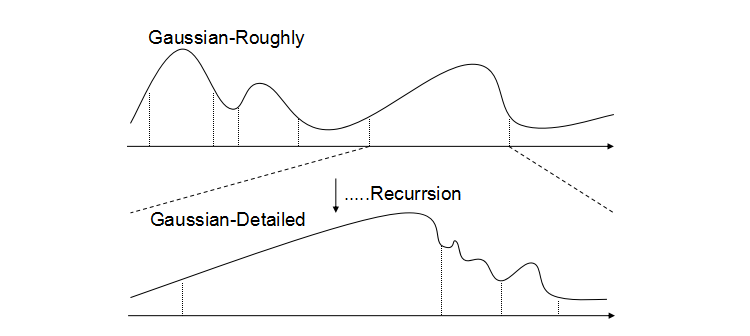
自动机寻峰的思路是这样的：

 

　　在对样本进行归一化处理和差分求导之后，根据对样本的观察，我们大致了解了这个样本之中峰的大致的形状，由此人工地去设定三个阈值作为自动机寻峰算法的参数：

　　

　　第一个参数是判断峰开始的斜率阈值

　　第二个参数是判断到达峰顶的斜率阈值

　　第三个参数是判断峰结束的斜率阈值

　　

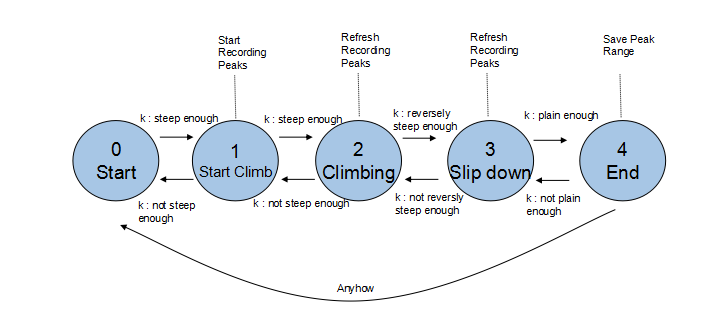
　　设定这三个阈值是为了防止数据中的快速抖动（平滑/“降噪“后也难以避免）导致自动状态的错误或者出现过多细碎的"小峰"的状况，如下图所示是自动机的状态转换图：

　　　　

　　下图是一次自动机寻峰之后的处理结果：

　　

 　　

以下是这个算法对几个不同的样本区间进行处理的结果plot图：

　　　　

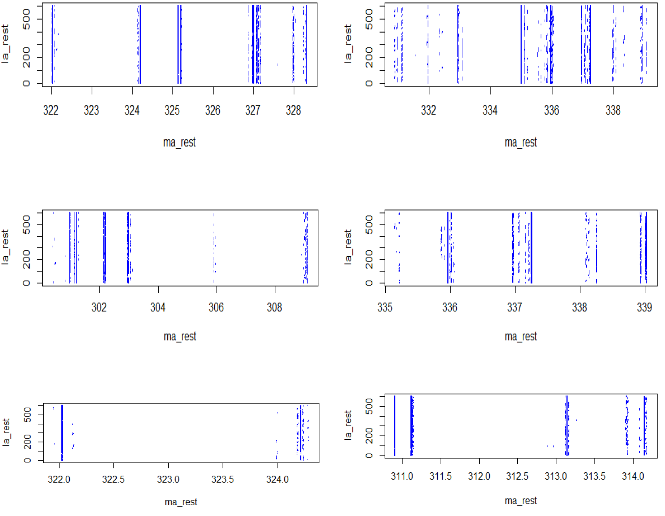
以及过滤比和加速比的结果：

 

　　　　　　

 

 

实现代码（R实现）：

 

　　由于项目中的一些其他原因，尽管这个算法表现不错，但最后也没有运用到项目中去，也就没有深入去做优化和修改。

　　R代码在我的github中：　　https://github.com/yue9944882/R_Util/tree/master/FSM_scan_peak

 

　　想更细节了解欢迎联系我的邮箱或者评论！