算法学习总结(六)：堆排序

一、算法简介

　　堆排序利用了大根堆（或小根堆）堆顶记录的关键字最大（或最小）这一特征，使得在当前无序区中选取最大（或最小）关键字的记录变得简单。

二、算法描述

1、什么是堆？

      我们这里提到的堆一般都指的是二叉堆，它满足二个特性：

           1---父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

           2---每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

     如下为一个最小堆(父结点的键值总是小于任何一个子节点的键值)

2、什么是堆调整(Heap Adjust)？

        这是为了保持堆的特性而做的一个操作。对某一个节点为根的子树做堆调整，其实就是将该根节点进行“下沉”操作(具体是通过和子节点交换完成的)，一直下沉到合适的位置，使得刚才的子树满足堆的性质。

       例如对最大堆的堆调整我们会这么做：

              1、在对应的数组元素A[i], 左孩子A[LEFT(i)], 和右孩子A[RIGHT(i)]中找到最大的那一个，将其下标存储在largest中。

              2、如果A[i]已经就是最大的元素，则程序直接结束。

              3、否则，i的某个子结点为最大的元素，将A[largest]与A[i]交换。

              4、再从交换的子节点开始，重复1,2,3步，直至叶子节点，算完成一次堆调整。

       这里需要提一下的是，一般做一次堆调整的时间复杂度为log(n)。

       如下为我们对4为根节点的子树做一次堆调整的示意图，可帮我们理解。

3、如何建堆

         建堆是一个通过不断的堆调整，使得整个二叉树中的数满足堆性质的操作。在数组中的话，我们一般从下标为n/2的数开始做堆调整，一直到下标为0的数(因为下标大于n/2的数都是叶子节点，其子树已经满足堆的性质了)。下图为其一个图示：

　　很明显，对叶子结点来说，可以认为它已经是一个合法的堆了即20，60， 65， 4， 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30，A[2] = 17，A[1] = 12，A[0] = 9分别作一次向下调整操作就可以了。

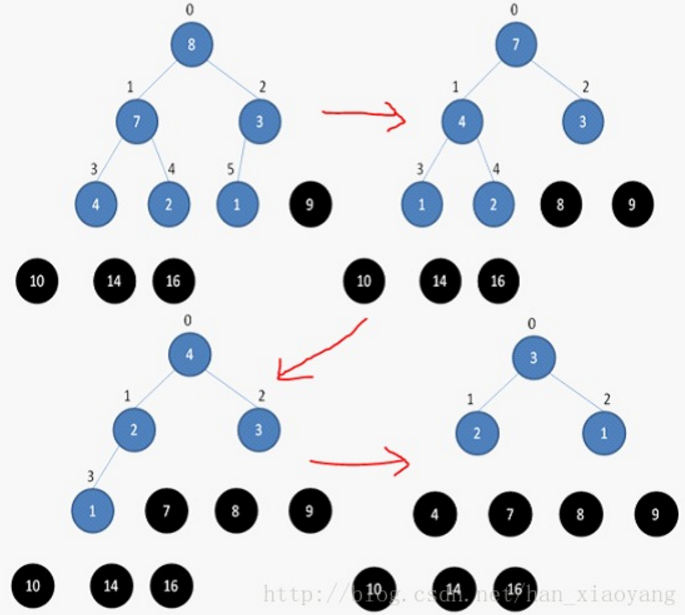
 4、如何进行堆排序

        堆排序是在上述3中对数组建堆的操作之后完成的。

        数组储存成堆的形式之后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n-2]交换，再对A[0…n-3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。

如下图所示：

 

最差时间复杂度	O(n log n)
最优时间复杂度	O(n log n)
平均时间复杂度	O(n log n)
最差空间复杂度	需要额外辅助空间O(n)

 

三、示例代码

public class HeapSort {
    public int[] heapSort(int[] A, int n) {
        // write code here
        for(int i=n/2; i>=0; i--){
            heapAdjust(A,i,n);
        }
        
        for(int i=n-1;i>0;i--){
            swap(A,0,i);
            heapAdjust(A,0,i);
        }
        return A;
    }
    
    void heapAdjust(int[] A,int index,int length){
        int childLeft;
        int temp = A[index];
        for( ;index*2+1 < length;index = childLeft){
            childLeft = index*2+1;
            if(childLeft !=length-1 && A[childLeft] < A[childLeft+1]){
                 childLeft++;
            }
            if(temp > A[childLeft]){
                break;
                
            }                
            else {
                A[index] = A[childLeft];
                index = childLeft;
            }           
        }
         A[index] = temp;
        
    }
    
    static void  swap(int[] A,int m,int n){
        int temp = A[m];
        A[m] = A[n];
        A[n] = temp;
    }
}