深度学习中的正则化

       

       在做机器学习的项目中，常常会出现这么一个常见而又头痛问题: 训练出来的模型效果不够好。这可怎么办呢？ 不着急，本文分析了这个问题的几种类型，并对其中一种类型介绍一种解决办法：正则化。

       先讲一个故事: 老师给你布置了一个人脸识别的问题，你很快做出了一个模型。很快你发现你的模型在训练集上准确率很高，达到99%, 但是在测试集上的准确率只有85%。你的这种情况说明你的模型方差过大。而与此同时，实验室的另一位同学在训练集和测试集上效果都只有87%,这个同学的模型偏差过大。

       偏差过大的原因一般是模型的泛化能力弱，如果是dnn，那么需要考虑从网络结构方面优化，如用较深较复杂的网络。

       方差过大的原因一般是模型过拟合了。过拟合主要从两方面来优化模型: 1,增大数据量。 2,对模型正则化。下面就主要介绍深度学习常用的正则化方法。

   1、L2正则化

       假设正则化前，损失函数$Loss=C_0$,加上 L2正则化后:

              $Loss=C_{0} + |w|_2$

                       $=C_{0} + \frac{\lambda}{2} \sum_{k=1}^N {w_i}^2 $

       这里$\lambda$是正则项的惩罚参数，$\lambda$越大惩罚程度也越大。$w_i$ 是每个权重的大小，这个公式中一共有 N 个参数。好了，到这里我们已经有了加入L2正则化的目标函数，然后就可以去求梯度了。有了梯度之后，我们就可以用经典的梯度下降法去解这个目标函数。哈哈，这个问题就算解决了。

       等等，好像哪里不太对。我们好像忽略了最本质的问题。那就是没有解释为什么 L2正则可以防止过拟合。想要明白这个问题，我们需要对$w_i$进行分析。首先看下$Loss$对$w_i$的导数:

               $\frac {\partial Loss}{w_i} = \frac{\partial C_0}{w_i} + {\lambda}{w_i}$

       求导后继续对$w_i$更新:

                $w_i=w_i - \eta(\frac{\partial C_0}{w_i} +  {\lambda}{w_i})$

                     $=(1-\eta{\lambda}){w_i} - \eta(\frac{\partial C_0}{w_i})$

       由于$1-\eta{\lambda}$小于1，可以看出$w_i$在梯度下降的过程中先进行$1-\eta{\lambda}$倍的衰减，这就是权重衰减的由来。

       至此我们解释了 L2正则可以让权重衰减，但依旧没有解释为什么衰减可以降低过拟合。首先给出直观的解释: 权重绝对值小说明模型简单，根据"奥姆剃须刀"的说法，越简单的模型越不容易过拟合。但是这样的说法往往很难让人信服。接下来从梯度的角度进行解释: 过拟合往往是因为模型过于考虑数据集中的每一个样本了。考虑的"面面俱到"就会致使模型复杂化，复杂化体现在在一些点上模型的梯度很陡峭。由于输入数据是不变的，为了拟合出这个陡峭的梯度，模型的参数的绝对值很可能就变得很大。而 L2正则正是通过权重衰减来降低模型过拟合的。

   2、L1正则化

        L1正则化与 L2的正则化的区别是: L1正则项用的一阶范式:

                 $Loss = C_0 +  |w|_1$

                          $=C_0 +  {\lambda} \sum_{k=1}^N {|w_i|}$  

        同样的也对$Loss$进行求导:

                 $\frac {\partial Loss}{w_i} =  \frac {\partial C_0}{w_i} + \lambda sign(w_i)$

        与 L2正则一样，这里进行权重更新:

                 $w_i = w_i - \eta (\frac{\partial C_0}{w_i} + \lambda sign(w_i))$ 

                      $=(w_i - \eta \lambda sign(w_i)) - \eta \frac{\partial C_0}{w_i}$

        当 $w_i > 0$时: $w_i = (w_i - \eta \lambda) - \eta \frac{\partial C_0}{w_i}$

        当 $w_i < 0$时: $w_i = (w_i + \eta \lambda) - \eta \frac{\partial C_0}{w_i}$

        可以发现参数更新时在减去"不加入正则的梯度前"总喜欢先往0靠近，这就解释了为什么 L1正则化后训练出的参数比较稀疏。L1正则同样起到了控制模型参数不使其太大，起到了防止过拟合作用，原理和 L2正则相同。

        这里从权重$w_i$更新的角度解释了 L1正则容易得到稀疏参数的现象。下面给出第二种解释从$Loss$最优化的角度进行解释。

                 $Loss(w) = C(w) + R(w) $

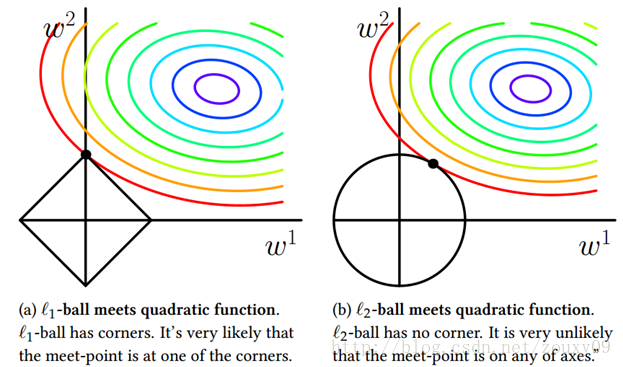
        这里$C(w)$ 表示不加正则化的损失函数，$R(w)$表示正则化函数。 我们把$Loss$当成两个函数$C(w)$和$R(w)$两个函数加和的时候，那么$Loss(w)$的极值一定在函数 $-C(w)$ 和 $R(w)$"相切"(之所以加引号，是因为当不可导时极值可以在边界)的地方。这张图是 PRML 里边的一样图: 这个图片里只考虑了2个参数的情况。 这里边黑色的是 $R(w)$的等高线，彩色的是$-C(w)$的等高线。由于L2正则化时$R(w)$的等高线很"圆滑"，所以它们"相切"的地方很难落在坐标轴上。 而 L1正则时，等高线有"角", 它们"相切"时比较容易落在"角"上，而这个"角"就在坐标轴上，所以 L1正则化时得到的参数比较稀疏。 

                                                                

      3、Dropout

         Dropout 是计算机视觉领域非常重要的一种正则化方法。这里先介绍 Dropout 的具体方法，然后介绍为什么 Dropout 是正则化。

         Dropout 是计算机视觉领域非常重要的一种正则化方法。这里先介绍 Dropout 的具体方法，然后介绍为什么 Dropout 是正则化。Dropout 本质很简单，就是在每次 batch训练的时候对一些层以一定的概率随机去掉神经元。下面神经网络一共有四层，每次训练的时候以一定的概率$keep\_pro$随机移出相应的神经元和与神经元相连的边。为了保持得到结果的公平，每个神经元计算得到的$z^{l}_{i}$需要除以$keep\_pro$。

         需要注意的时每一层的$keep\_pro$可以不一样。而且在使用训好的模型时不需要 Dropout。

                                                                          

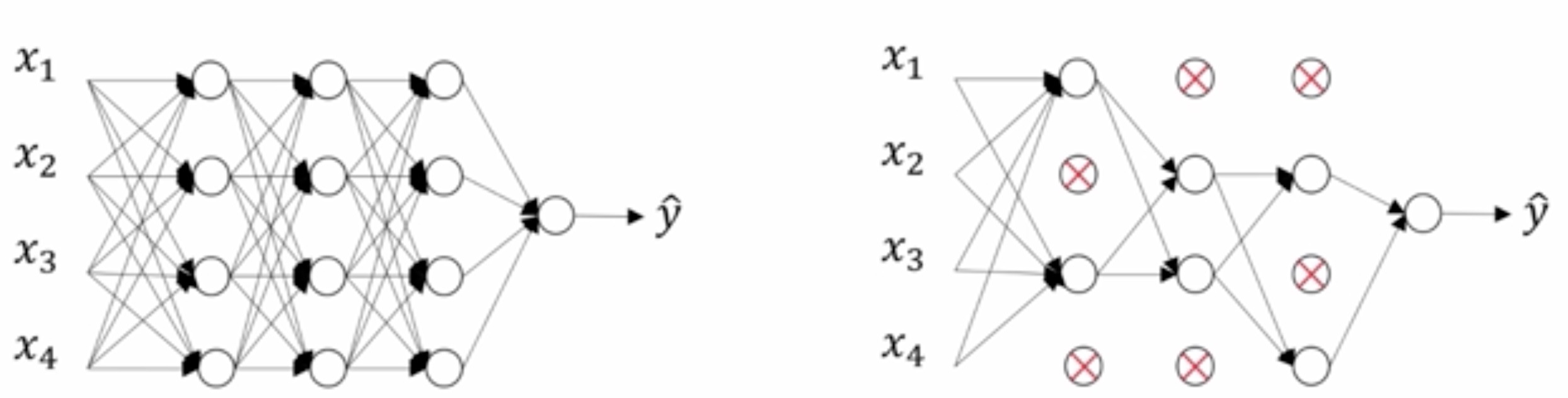
        是不是很简单呀。可能你还会觉得很 amazing，这随机删除一些结构居然还能起到正则化的作用?  其实 Dropout 的思想是在神经网络中不严重依赖某一个特定的神经元。每一个神经元都可能被移出，所以模型不会过分的将权重分配在某个特定神经元上。这与 L2正则很像，如果某个参数的权值过高，模型具有对参数打压的机制。 因此说，Dropout 是一种正则化方法。这里提下，对于计算机视觉问题的目标来讲，数据量往往不够，因此在解决计算机视觉问题的时候很容易发生过拟合。Dropout 作为一种正则化方法在计算机视觉上往往有很好的效果。