线索二叉树（先序/中序/后续 图解+代码）

一、问题引入

在二叉树中存在以下两个问题：

  • \(n\)个结点的二叉树，有\(n+1\)个空链域

    对于具有\(n\)个结点的二叉树，当采用二叉链存储结构时，每个结点有两个指针域，总共有\(2n\)个指针域。只有\(n-1\)个结点被有效指针域所指向(\(n\)个结点中只有根节点没有被有效指针域指向)。所以共有\(2n-(n-1)=n+1\)个空链域。

  • 二叉树的遍历效率不高。

    在普通二叉树中，每个节点的遍历可能需要递归调用或者使用栈来存储节点，这在最坏的情况下会占用较多的空间，并且递归调用可能有较大的开销。

遍历二叉树的的结果是一个结点的线性序列。图中二叉树的中序遍历的结果为：\(DGBAECF\)。可以利用这些空链域存放指向结点的前驱结点和后继结点的地址。这些“前驱结点”和“后继节点”的指针称为线索。

二叉树

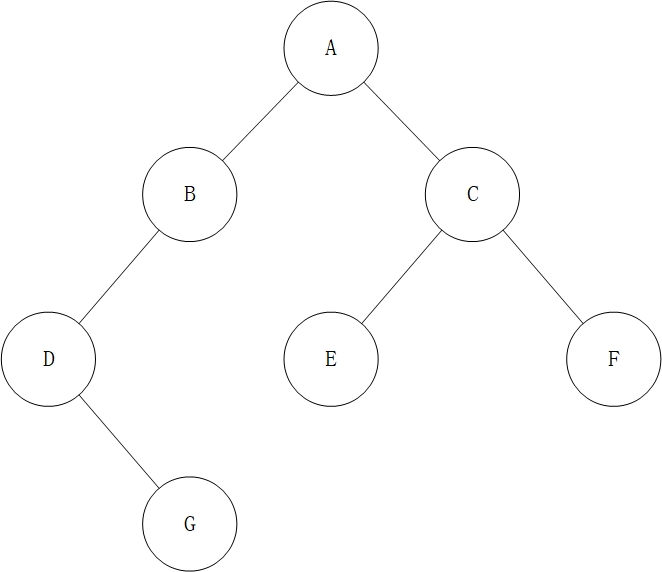
创建线索的过程成为线索化。线索化的二叉树称为线索二叉树。

二、线索二叉树

规定：某结点的左指针为空时，令该指针指向这个线性序列中该结点的前驱结点；某结点的右指针为空时，令该指针指向这个线性序列中该结点的后继节点。

为了区分左指针指向的是左孩子结点还是前驱结点，右指针指向的是右孩子结点还是后继节点，在此结点上添加两个标志位来区分这两种情况。

\[左标志 ltag=\begin{cases} 0,&表示lchild指向左孩子结点\\ 1, &表示lchild指向前驱结点\end{cases} \]

\[右标志rtag=\begin{cases} 0, & 表示rchild指向右孩子结点 \\ 1,& 表示rchild指向后继结点\end{cases} \]

这样，每个结点的存储结构如下：

ltag lchild data rchild rtag

为了使创建线索二叉树的算法设计方便，在线索二叉树中再增加一个头节点。

头结点的\(data\)域为空；\(lchild\)指向无线索时的根节点，即原本二叉树的根结点，\(ltag\)为\(0\);\(rchild\)指向按某种方式遍历二叉树的最后一个结点,\(rtag\)为1.

这样在线索二叉树中没有空指针域。

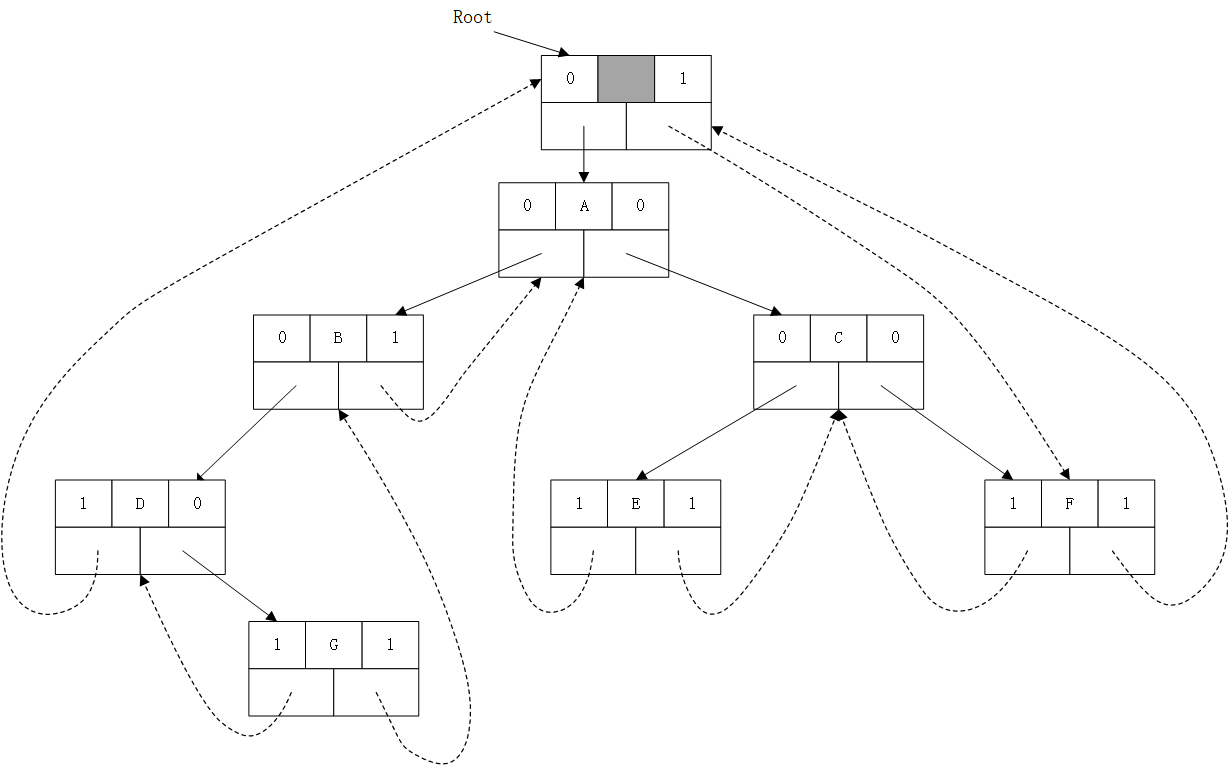
如下图所示，为中序线索二叉树。

中序线索树

三、设计实现

3.1 结点类型

根据前面的分析，线索二叉树的结点应包含以下内容：

typedef char ElemType;
typedef struct node
{
    ElemType data;		//结点数据域
    bool ltag, rtag;	//增加线索的标记
    struct node *lchild;//左孩子或前驱线索指针
    struct node *rchild;//右孩子或后驱线索指针
} TBTNode;

3.2 中序线索树

根据前面分析，当一个结点\(p\)没有左孩子时，它的左指针应该指向结点\(p\)的前驱结点。那么不妨用一个变量\(pre\)表示。

即：结点\(p\)表示当前访问的结点，结点\(pre\)总是指向刚访问过的结点。初始化\(pre=root\)。

采用类似中序遍历的递归算法来构造线索二叉树。

先线索化左子树，再线索化该节点，最后线索化右子树。

对于每个结点\(p\)都考虑以下步骤：

  1. 递归处理左子树：首先，对结点\(p\)的左子树进行递归处理，直到结点\(p\)没有左孩子。
    • 在这个过程中，如果结点\(p\)没有左孩子，它将成为中序遍历中的第一个结点。
  2. 处理左孩子结点
    • 如果当前结点\(p\)有左孩子结点，则将标记\(ltag\)设为\(0\)，即\(p\to ltag=0\)
    • 如果当前结点\(p\)无左孩子结点，则\(p\)的左指针应指向前驱结点\(pre\)，并将标记\(ltag\)设为\(1\),即\(p\to lchild=pre,p\to ltag=1\)
  3. 更新前驱结点的线索
    • 如果前驱结点\(pre\)有右孩子结点，则将标记\(rtag\)设为\(0\)，即\(pre\to rtag=0\)
    • 如果前驱结点\(pre\)无右孩子结点，则\(pre\)的右指针应指向后继结点\(p\),并将标记\(rtag\)设为\(1\)，即\(pre\to rchild=p,pre\to rtag=1\)
  4. 更新前驱结点
    • 接下来要处理\(p\)的后继节点，所以要更改\(pre=p\)
  5. 递归处理右子树

以上面中序线索二叉树为例解释一下：

从结点\(root\)开始,找到根节点\(A\)。

从结点\(A\)开始递归，结点\(A\)有左孩子\(B\)，进入结点\(B\).

结点\(B\)有左孩子结点\(D\)，进入结点\(D\).

结点\(D\)无左孩子，则它的左指针应该指向\(pre\),即\(p\to lchild=pre\).

注意这理\(pre->rchild=p\)，即\(root\)的右指针会指向结点\(D\),与图中不符。这里只因为后续将会更改\(root\)的右指针，使之指向中序遍历的最后一个结点。

更新\(pre=p\).递归右子树，来到结点\(G\).无左右孩子结点，则左指针指向前驱结点\(pre\),即指向结点\(D\)。\(pre\)有右孩子结点，则更新标记\(rtag\)为\(0\).

更新\(pre\)，此时指向结点\(G\)

回归到结点\(B\),它有左孩子结点，所以更新标记\(ltag\)为\(0\)。前驱结点\(pre\)无右孩子结点，指向结点\(B\).即结点\(G\)的右指针指向结点\(B\).

...

代码实现：


TBTNode *pre; // 全局遍历，前驱结点

void Thread(TBTNode *&p) // 中序线索化二叉树，被CreateThread调用
{
    if (p == NULL)
        return;
    Thread(p->lchild);     // 左子树线索化
    if (p->lchild == NULL) // 左子树为空
    {
        p->lchild = pre; // 指向前驱结点pre
        p->ltag = 1;
    }
    else
        p->ltag = 0;

    if (pre->rchild == NULL)
    {
        pre->rchild = p; // 指向后继结点p
        pre->rtag = 1;
    }
    else
        pre->rtag = 0;
    pre = p;
    Thread(p->rchild); // 右子树线索化
}

TBTNode *CreateThread(TBTNode *b)
{
    TBTNode *root = new TBTNode;
    root->ltag = 0, root->rtag = 1; // 左孩子为二叉树，因此左标记为0.右孩子为空，因此为1.
    root->lchild = b;
    if (b == NULL) // 空二叉树
        root->lchild = root;
    else
    {
        root->lchild = b;
        pre = root;
        Thread(b);
        pre->rchild = root; // pre是二叉树最后访问的结点，右子树指向头节点
        pre->rtag = 1;
        root->rchild = pre; // 头节点线索化
    }
    return root;
}

3.3 先序线索树

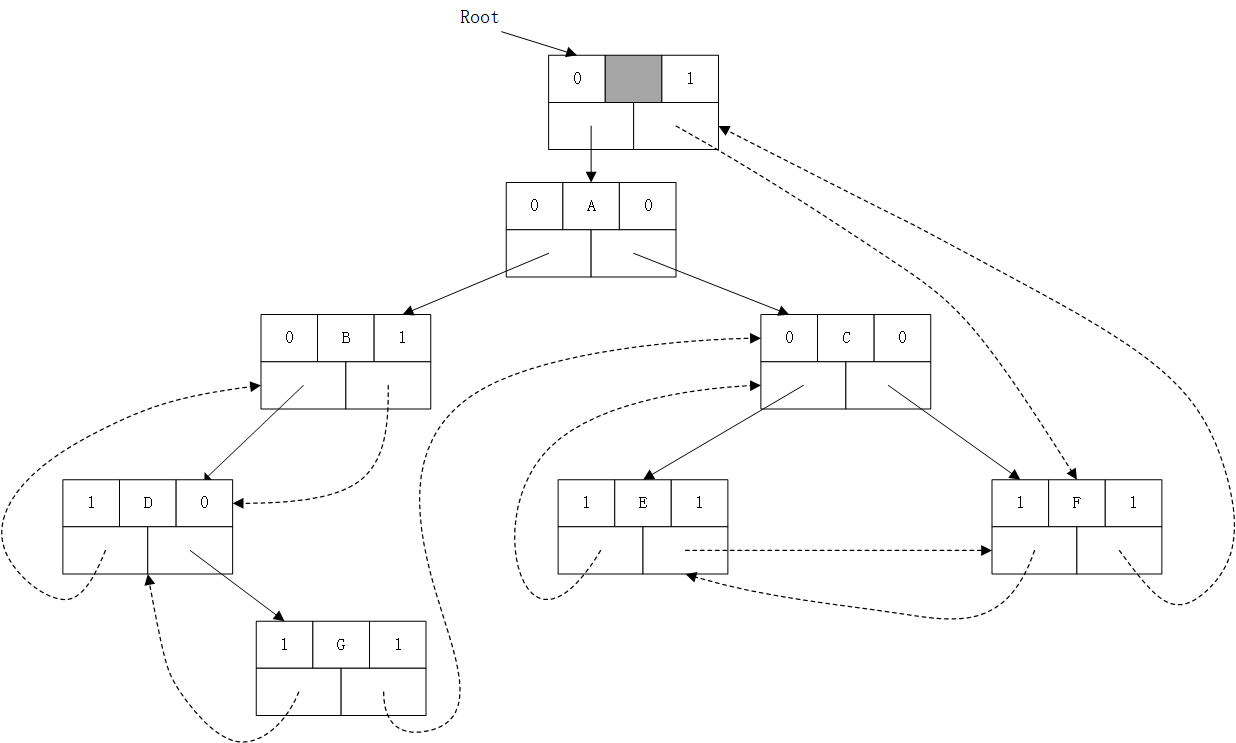
先序线索树

与中序线索树的构造方式类型。

令\(p\)结点表示当前结点，\(pre\)表示上一个访问的结点，然后按照先序遍历的方式构造线索。

先处理当前结点的信息，然后再递归左右子树。

当结点\(p\)没有左孩子或者右孩子时，会因为前面的操作，导致指针不为空，直接递归会导致死循环。

在递归之前先判断是否为左孩子。若标记\(tag\)为\(0\),则为孩子结点，反之，则为线索。

代码实现：


void ProOrderThread(TBTNode *&p) // 先序线索化二叉树
{

    if (p == NULL)
        return;
    if (p->lchild == NULL) // 左子树为空，则为线索
    {
        p->lchild = pre;
        p->ltag = 1;
    }
    else
        p->ltag = 0;
    if (pre->rchild == NULL) // pre的右子树为空，则为线索
    {
        pre->rchild = p;
        pre->rtag = 1;
    }
    else
        pre->rtag = 0;
    pre = p;          // 先更新pre
    if (p->ltag == 0) // 如果存在左孩子，则访问。不加判断 会陷入死循环
        ProOrderThread(p->lchild);
    if (p->rtag == 0) // 判断是否存在右孩子
        ProOrderThread(p->rchild);
}

TBTNode *CreateProOrderThread(TBTNode *b)
{
    TBTNode *root = new TBTNode; // 创建头结点
    root->ltag = 0, root->rtag = 1;
    root->lchild = b;
    if (b == NULL) // 二叉树为空
        root->lchild = root;
    else
    {
        root->lchild = b;
        pre = root;
        ProOrderThread(b);  // 线索化二叉树
        pre->rchild = root; // pre是最后一个结点，令它的右指针指向头结点
        pre->rtag = 1;
        root->rchild = pre; // 头结点的右指针指向最后一个结点
    }
    return root;
}

3.4 后续线索树

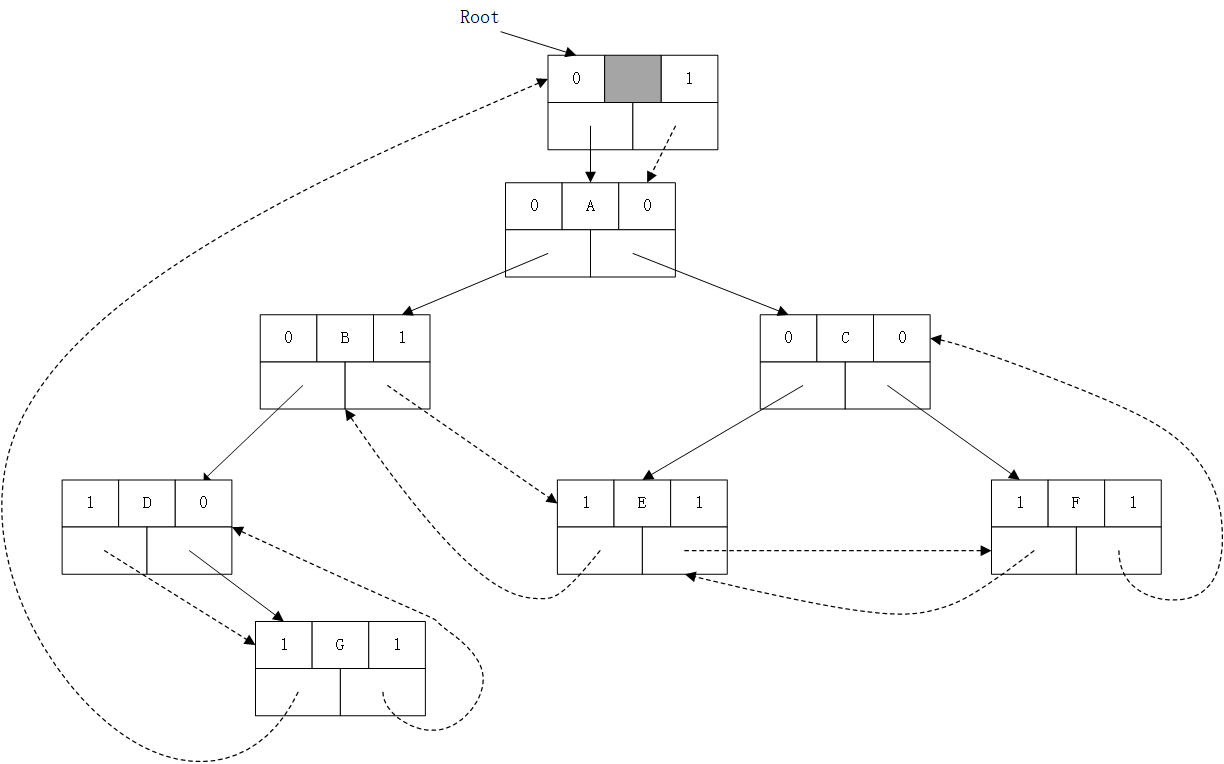
后序线索树

与前两种的思路一致。

按照后序遍历的方式构造线索。

先线索化左右子树，再线索化该节点。

代码实现：

void PostorderThread(TBTNode *&p)
{
    if (p == NULL)
        return;
    PostorderThread(p->lchild);
    PostorderThread(p->rchild);

    cout << p->data;
    if (p->lchild == NULL)
    {
        p->lchild = pre;
        p->ltag = 1;
    }
    else
        p->ltag = 0;

    if (pre->rchild == NULL)
    {
        pre->rchild = p;
        pre->rtag = 1;
    }
    else
        pre->rtag = 0;
    pre = p;
}

TBTNode *CreatePostorderThread(TBTNode *b)
{
    TBTNode *root = new TBTNode;
    root->ltag = 0, root->rtag = 1;
    root->lchild = b;
    if (b == NULL)
        root->lchild = root;
    else
    {
        root->lchild = b;
        pre = root;
        PostorderThread(b);
        pre->rtag = 1;
        root->rchild = pre;
    }
    return root;
}

四、遍历实现

4.1 中序线索树

先找到开始结点，然后访问开始结点\(p\)。

如果结点\(p\)的右指针是右线索，说明右线索指向的是后继结点，就跳到后继结点继续遍历；

如果结点\(p\)的右指针不是右线索，它指向的是右子树，就转向右子树，右子树的遍历遍历对整个二叉树的遍历是相似的。

整个过程描述如下：

p指向根节点：
while p!=root时循环
{
	找开始结点p;
    访问p结点;
    while(p结点有线索)
    	一直访问下去;
    p转向右孩子结点;                        //不是右线索的情况
}

代码实现：

void ThInOrde(TBTNode *tb)
{
    TBTNode *p = tb->lchild; // p指向根节点
    while (p != tb)
    {
        while (p->ltag == 0)
            p = p->lchild;

        cout << p->data;
        while (p->rtag == 1 && p->rchild != tb)
        {
            p = p->rchild;
            cout << p->data;
        }
        p = p->rchild;
    }
}

4.2 先序线索树

与中序二叉树的遍历方式相似。

第一个结点即为开始结点。

如果结点\(p\)的左指针是左子树，则跳转到左子树。

如果结点\(p\)右指针为右线索，则跳转到后继结点继续访问。

如果当前结点\(p\)有左子树则跳转到左子树，否则跳转右子树。

过程描述如下：

p指向根节点：
while p!=root时循环
{
	访问结点p;
	while(p有左子树):
		一直访问下去;
	while(p有右线索):
		一直访问下去;
	if(p有左子树)					//此时结点p右指针一定是右子树，但在先序遍历中要先检查左子树
		访问左子树
	else
		访问右子树
}

代码实现：

void ThProOrde(TBTNode *tb)
{
    TBTNode *p = tb->lchild; // p指向根节点

    while (p != tb)
    {
        cout << p->data;
        while (p->ltag == 0)
        {
            p = p->lchild;
            cout << p->data;
        }

        while (p->rtag == 1 && p->rchild != tb)
        {
            p = p->rchild;
            cout << p->data;
        }
        if (p->ltag == 0)
            p = p->lchild;
        else
            p = p->rchild;
    }
}

4.3 后续线索树

当前设计下，在访问后续线索树时，无法通过非递归的方式访问结点的父节点，所以需要在结点添加\(parent\)指针，指向父节点。

此处略。

附：代码

#include <bits/stdc++.h>
using namespace std;

typedef char ElemType;

// 结点
typedef struct node
{
    ElemType data;
    bool ltag, rtag;
    struct node *lchild;
    struct node *rchild;
} TBTNode;

// 创建结点
TBTNode *CreateNode(ElemType data)
{
    if (data == 'X')
        return NULL;
    TBTNode *ans = new TBTNode;
    ans->data = data;
    ans->lchild = NULL;
    ans->rchild = NULL;
    return ans;
}

// 创建二叉树
void CreateTBTree(TBTNode *&b, string str)
{
    int pos = 0;
    b = CreateNode(str[pos++]);
    queue<TBTNode *> que;

    que.push(b);
    while (pos < str.size())
    {
        TBTNode *head = que.front();

        que.pop();
        if (head == NULL)
            continue;

        head->lchild = CreateNode(str[pos++]);
        que.push(head->lchild);

        head->rchild = CreateNode(str[pos++]);
        que.push(head->rchild);
    }
}

// 中序遍历
void InorderTraversal(TBTNode *b)
{
    if (b == NULL)
        return;
    if (b->lchild)
    {
        InorderTraversal(b->lchild);
    }
    cout << b->data;
    if (b->rchild)
    {
        InorderTraversal(b->rchild);
    }
}

// 先序遍历
void ProorderTraversal(TBTNode *b)
{
    if (b == NULL)
        return;
    cout << b->data;
    if (b->lchild)
        ProorderTraversal(b->lchild);
    if (b->rchild)
        ProorderTraversal(b->rchild);
}

TBTNode *pre; // 全局遍历，前驱结点

void InOrderThread(TBTNode *&p) // 中序线索化二叉树，被CreateThread调用
{
    if (p == NULL)
        return;
    InOrderThread(p->lchild); // 左子树线索化
    if (p->lchild == NULL)    // 左子树为空
    {
        p->lchild = pre; // 指向前驱结点pre
        p->ltag = 1;
    }
    else
        p->ltag = 0;

    if (pre->rchild == NULL)
    {
        pre->rchild = p; // 指向后继结点p
        pre->rtag = 1;
    }
    else
        pre->rtag = 0;
    pre = p;
    InOrderThread(p->rchild); // 右子树线索化
}
TBTNode *CreateInOrderThread(TBTNode *b)
{
    TBTNode *root = new TBTNode;
    root->ltag = 0, root->rtag = 1; // 左孩子为二叉树，因此左标记为0.右孩子为空，因此为1.
    root->lchild = b;
    if (b == NULL) // 空二叉树
        root->lchild = root;
    else
    {
        root->lchild = b;
        pre = root;
        InOrderThread(b);
        pre->rchild = root; // pre是二叉树最后访问的结点，右子树指向头节点
        pre->rtag = 1;
        root->rchild = pre; // 头节点线索化
    }
    return root;
}
// 遍历线索二叉树
void ThInOrde(TBTNode *tb)
{
    TBTNode *p = tb->lchild; // p指向根节点
    while (p != tb)
    {
        while (p->ltag == 0)
            p = p->lchild;

        cout << p->data;
        while (p->rtag == 1 && p->rchild != tb)
        {
            p = p->rchild;
            cout << p->data;
        }
        p = p->rchild;
    }
}

void ProOrderThread(TBTNode *&p) // 先序线索化二叉树
{

    if (p == NULL)
        return;
    if (p->lchild == NULL) // 左子树为空，则为线索
    {
        p->lchild = pre;
        p->ltag = 1;
    }
    else
        p->ltag = 0;
    if (pre->rchild == NULL) // pre的右子树为空，则为线索
    {
        pre->rchild = p;
        pre->rtag = 1;
    }
    else
        pre->rtag = 0;
    pre = p;          // 先更新pre
    if (p->ltag == 0) // 如果存在左孩子，则访问。不加判断 会陷入死循环
        ProOrderThread(p->lchild);
    if (p->rtag == 0) // 判断是否存在右孩子
        ProOrderThread(p->rchild);
}

TBTNode *CreateProOrderThread(TBTNode *b)
{
    TBTNode *root = new TBTNode; // 创建头结点
    root->ltag = 0, root->rtag = 1;
    root->lchild = b;
    if (b == NULL) // 二叉树为空
        root->lchild = root;
    else
    {
        root->lchild = b;
        pre = root;
        ProOrderThread(b);  // 线索化二叉树
        pre->rchild = root; // pre是最后一个结点，令它的右指针指向头结点
        pre->rtag = 1;
        root->rchild = pre; // 头结点的右指针指向最后一个结点
    }
    return root;
}

void ThProOrde(TBTNode *tb)
{
    TBTNode *p = tb->lchild; // p指向根节点

    while (p != tb)
    {
        cout << p->data;
        while (p->ltag == 0)
        {
            p = p->lchild;
            cout << p->data;
        }

        while (p->rtag == 1 && p->rchild != tb)
        {
            p = p->rchild;
            cout << p->data;
        }
        if (p->ltag == 0)
            p = p->lchild;
        else
            p = p->rchild;
    }
}

int main()
{
    string str = "ABCDXEFXGXXXX";
    TBTNode *b, *tb;
    CreateTBTree(b, str);
    ProorderTraversal(b);
    cout << endl;
    tb = CreateProOrderThread(b);
    cout << endl;
    ThProOrde(tb);
}
posted @ 2024-09-30 23:47  Gu_diao  阅读(548)  评论(0)  编辑  收藏  举报