unity三维地球模型生成

准备一张贴图

 

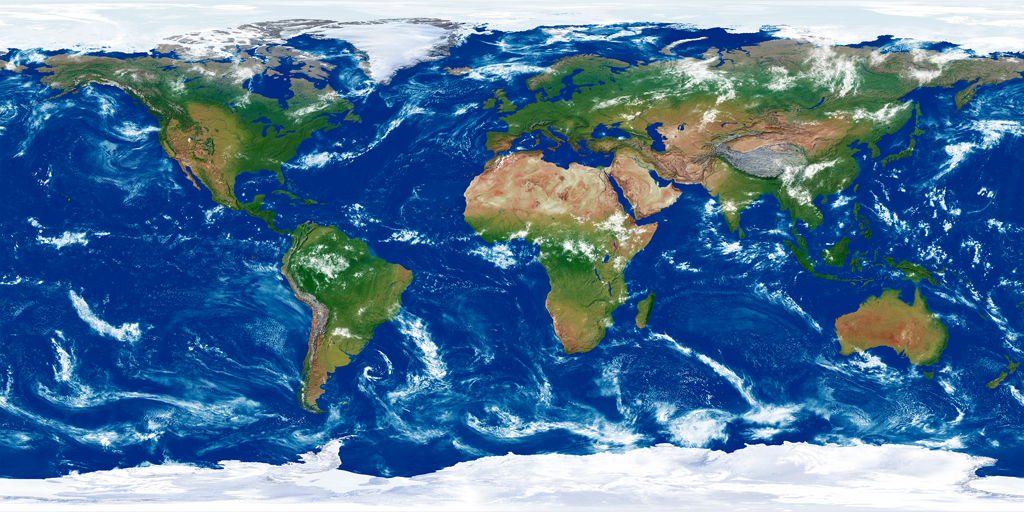
创建材质球

 

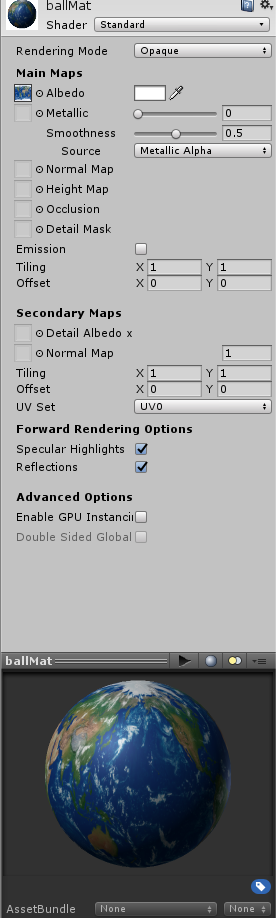
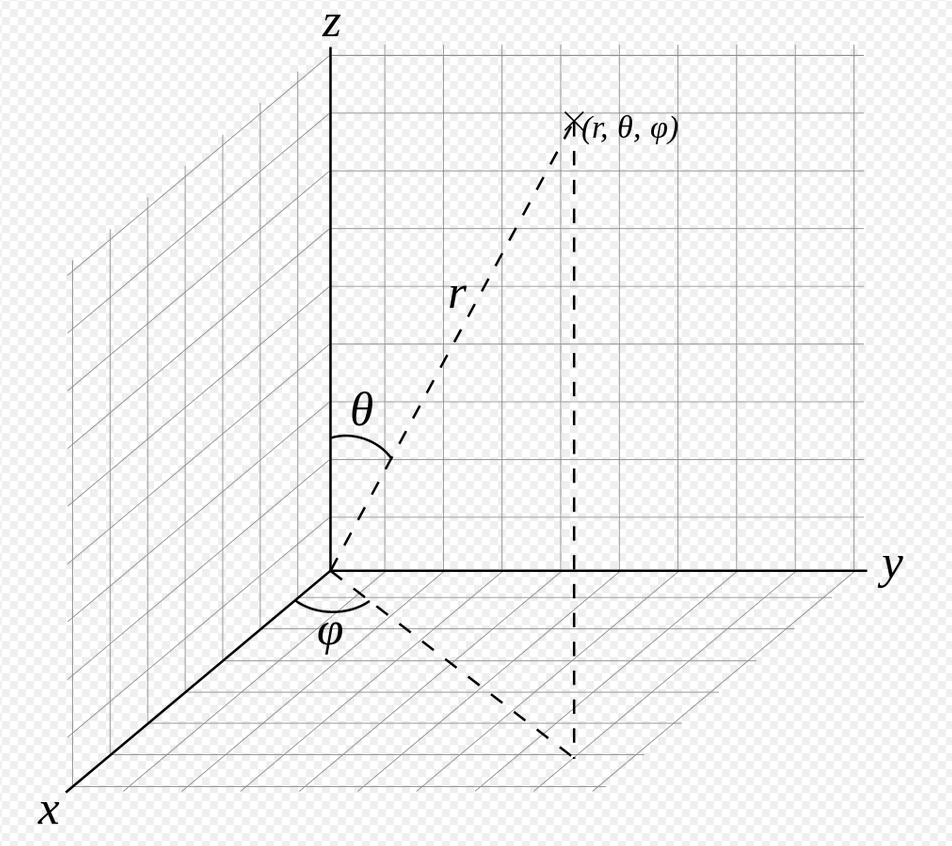
球面坐标系转直角坐标系

x=rsinθcosφ.

y=rsinθsinφ.

z=rcosθ.

效果如下

 

脚本如下

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

//创建球形mesh
public class BallCreater : MonoBehaviour {
    public Material ballMat;//材质
	void Start () {
        createBall("mEarth",new Vector3(0,0,0),100.0f,181,88);
    }

    void Update () {
		
	}
    /// <summary>
    /// 创建球形mesh
    /// </summary>
    /// <param name="meshName">名称</param>
    /// <param name="center">球心</param>
    /// <param name="radius">半径</param>
    /// <param name="longPart">经线数</param>
    /// <param name="latPart">纬线数</param>
    /// <returns></returns>
    private GameObject createBall(string meshName,Vector3 center, float radius, int longPart, int latPart)
    {
        GameObject meshObject = new GameObject(meshName);

        int verticeNum = longPart * latPart+2* longPart;//经线数*纬线数+极点处多个重合点 (首尾经线重合)
        Vector3[] vertices = new Vector3[verticeNum];//顶点数组 
        Vector3[] normals = new Vector3[verticeNum];//顶点法线数组
        Vector2[] uvs = new Vector2[verticeNum];//uv数组
        int[] triangles = new int[(longPart-1)* latPart * 3 * 2];//三角集合数组,保存顶点索引 

        float degreesToRadians = Mathf.PI / 180.0f; //弧度转换
        float deltaLong = 360.0f /(longPart-1);//经度每份对应度数
        float deltaLat = 180.0f/ (latPart+2);//纬度每份对应度数
        //极点放置多个顶点，同位置不同uv
        for (int i = 0; i < longPart; i++)
        {
            vertices[i] = new Vector3(0, 0, 1) * radius;
            normals[i] = vertices[0].normalized;
            uvs[i] = new Vector2((float)i/(float)longPart,0);
        } 
        int k = 0; 
        for (int i = 0; i < longPart-1; i++)
        {
            triangles[k++] = i; 
            triangles[k++] = i+ longPart;
            triangles[k++] = i + longPart+1;
        }  
        for (int tempLat = 0; tempLat < latPart; tempLat++) 
        { 
            float tempAngle1 = ((tempLat+1)* deltaLat) * degreesToRadians; 
            for (int tempLong = 0; tempLong < longPart; tempLong++) 
            {
                float tempAngle2 = (tempLong*deltaLong) * degreesToRadians; 
                int tempIndex = tempLong+ tempLat* longPart+ longPart; 
                vertices[tempIndex] = new Vector3(Mathf.Sin(tempAngle1) * Mathf.Cos(tempAngle2), Mathf.Sin(tempAngle1) * Mathf.Sin(tempAngle2), Mathf.Cos(tempAngle1)) * radius;
                normals[tempIndex] = vertices[tempIndex].normalized;
                uvs[tempIndex] = new Vector2((float)tempLong / (float)longPart, (float)tempLat / (float)latPart);
                if (tempLat!= latPart-1)
                {
                    if (tempLong != longPart-1)
                    {
                        triangles[k++] = tempLong + tempLat * longPart + longPart;
                        triangles[k++] = tempLong + tempLat * longPart + 2 * longPart;
                        triangles[k++] = tempLong + tempLat * longPart + longPart + 1;

                        triangles[k++] = tempLong + tempLat * longPart + 2 * longPart;
                        triangles[k++] = tempLong + tempLat * longPart + 1 + 2 * longPart;
                        triangles[k++] = tempLong + tempLat * longPart + 1 + longPart;

                    } 
                }  
            } 
        }
        //极点放置多个顶点，同位置不同uv
        for (int i = 0; i < longPart; i++)
        {
            vertices[verticeNum - 1-i] = new Vector3(0, 0, -1) * radius;
            normals[verticeNum - 1-i] = vertices[verticeNum - 1].normalized;
            uvs[verticeNum - 1-i] = new Vector2(1.0f-(float)i / (float)longPart, 1.0f); 
        } 
        for (int i = 0; i < longPart-1; i++)
        {
            triangles[k++] = verticeNum - 1-i; 
            triangles[k++] = verticeNum - 1-i- longPart;
            triangles[k++] = verticeNum - 2 - i- longPart;
        } 

        Mesh mesh = new Mesh();
        mesh.vertices = vertices;
        mesh.triangles = triangles;
        mesh.normals = normals;
        mesh.uv = uvs;
        mesh.RecalculateBounds();
        mesh.RecalculateNormals();
        meshObject.AddComponent<MeshFilter>();
        meshObject.AddComponent<MeshRenderer>();
        meshObject.GetComponent<MeshFilter>().mesh = mesh;
        meshObject.GetComponent<MeshRenderer>().material = ballMat;
        meshObject.transform.position += center;
        return meshObject;
    }

}

 

本文链接 https://www.cnblogs.com/gucheng/p/10121903.html