ALV平衡树实现
1.1 基本介绍
平衡二叉树又称AVL树,是一种最早的自平衡二分搜索树结构,它是具有如下性质的二叉树:
- 左、右子树是平衡二叉树;
- 所有结点的左、右子树深度之差的绝对值≤1。
- 满二叉树一定是平衡二叉树,高度最低。
- 完全二叉树也是平衡二叉树,叶子节点深度相差不为1
为了方便起见,给每个结点附加一个数字 = 该结点左子树与右子树的深度差。这个数字称为结点的平衡因子。这样,可以得到AVL树的其它性质(可以证明) :
任一结点的平衡因子只能取: -1、0、1,如果树中任意一个结点的平衡因子的绝对值大于1,则这棵二叉树就失去平衡。
1.2 LL平衡旋转
1、思路分析
插入的元素在不平衡的节点的左侧。
节点大小:T1 < z < T2 < x < T3 < y < T4
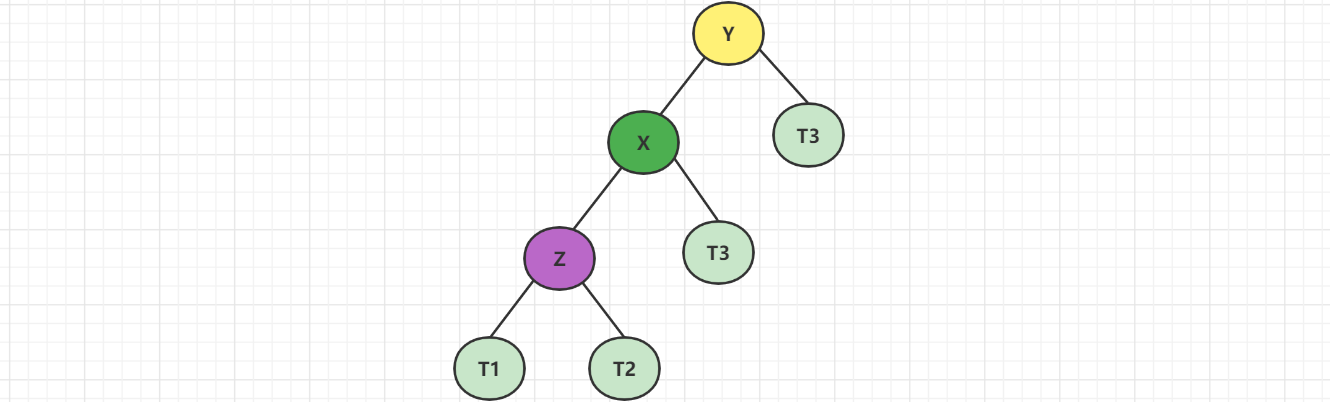
先让X的右子树变成以Y为根的子树,再让Y的左子树变成x的右子树。然后让X变成新的二叉树的根节点。
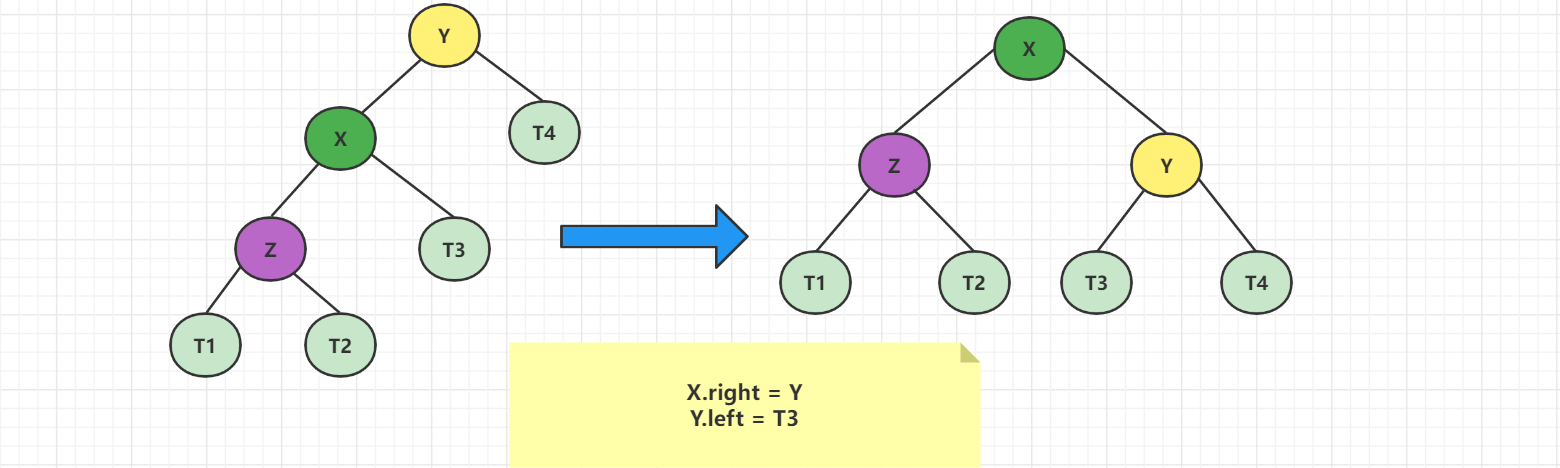
2、案例实现
以B为轴,对A做了一次单向右旋平衡旋转。
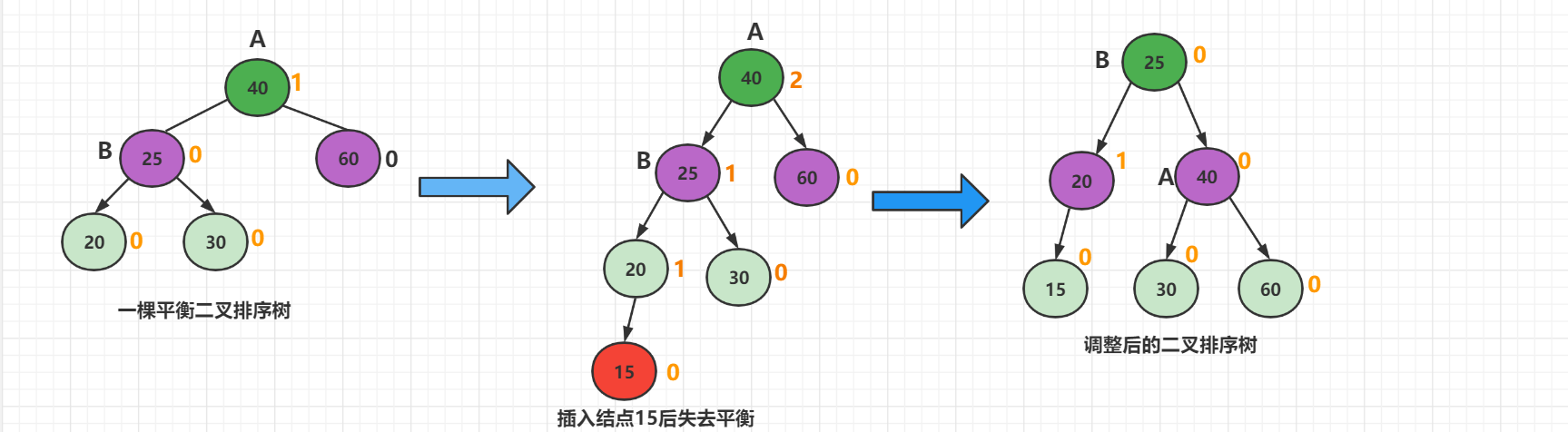
1.3 RR平衡旋转
1、思路分析
插入的元素在不平衡的节点的右侧的右侧。
节点大小:T4 < Y < T3 < x < T1 < Z < T2
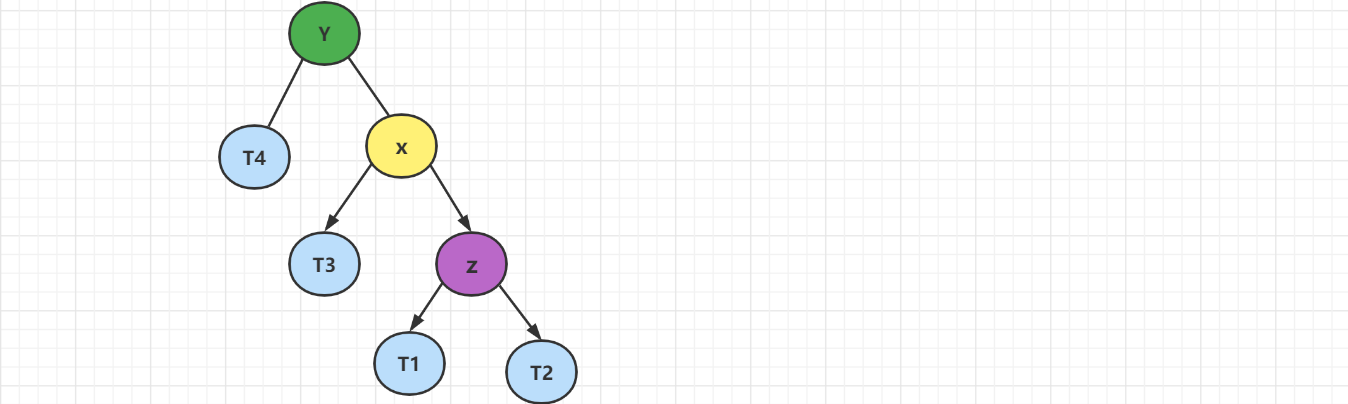
先让X的左子树变成以Y为根的子树,再让Y的右子树变成x的左子树
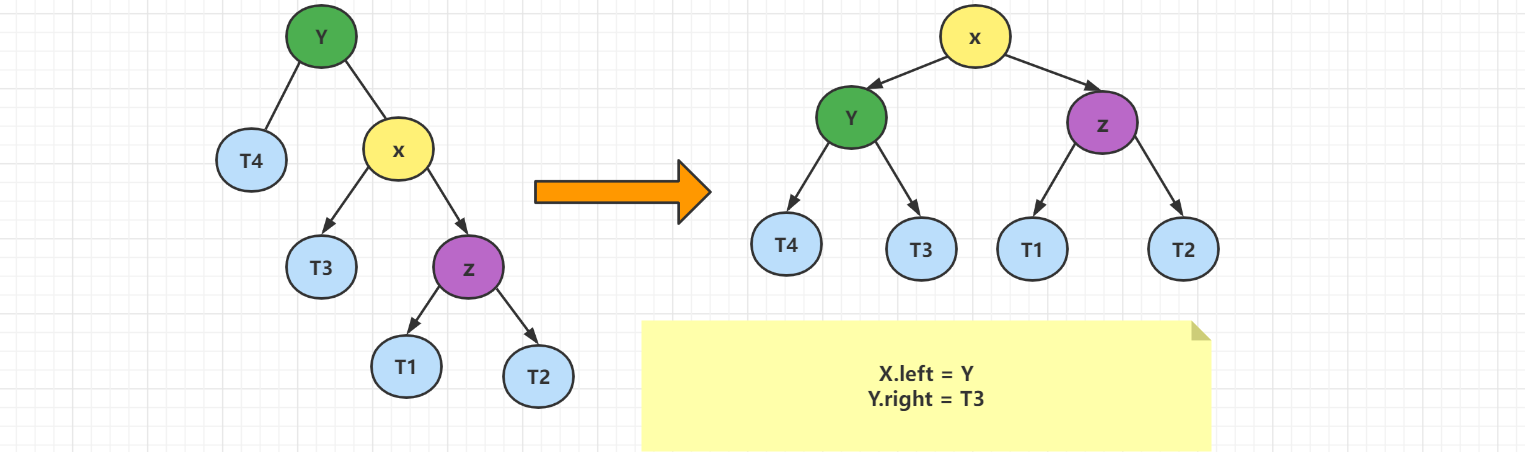
2、案例实现
以B为轴,对A做了一次单向左旋平衡旋转。
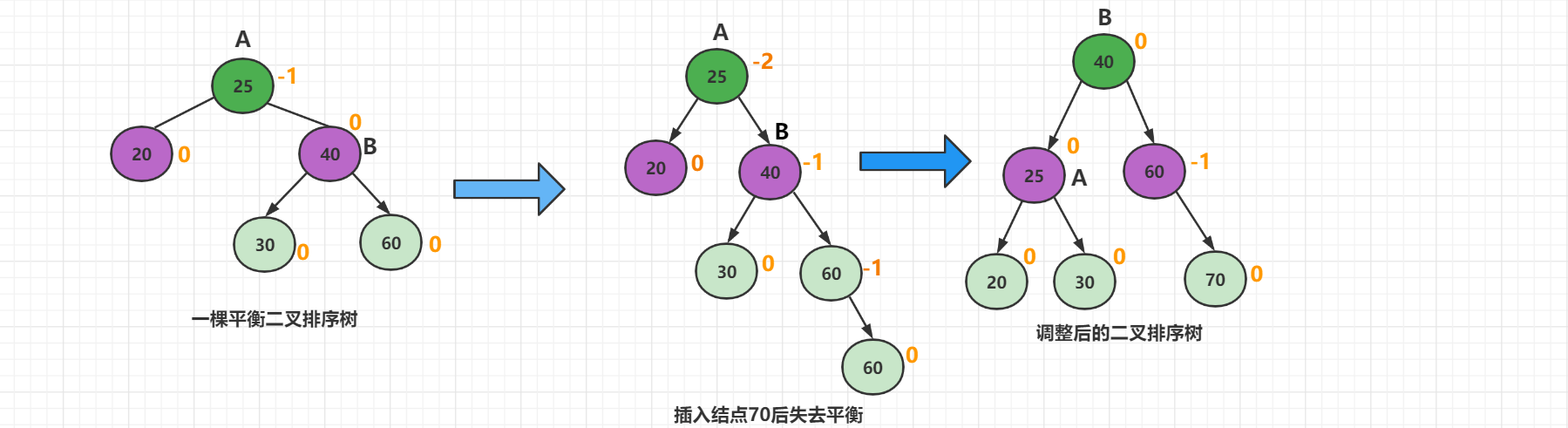
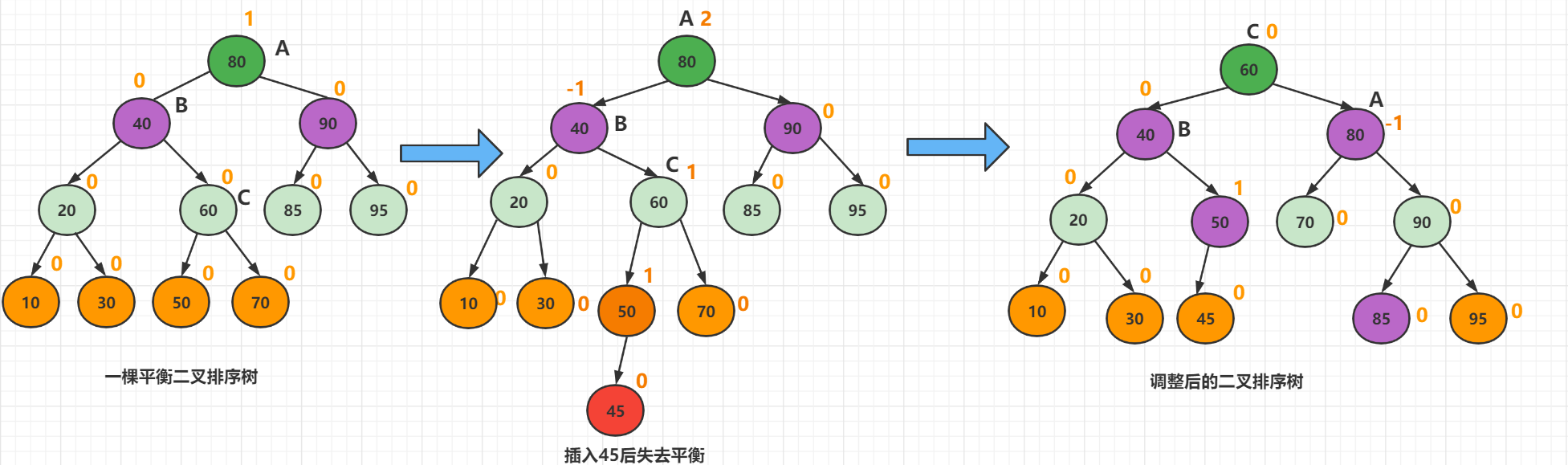
1.4 LR平衡旋转
1、思路分析
插入的元素在不平衡的节点的左侧的右侧。
节点大小:T1 < x < T2 < z < T3 < y < T4
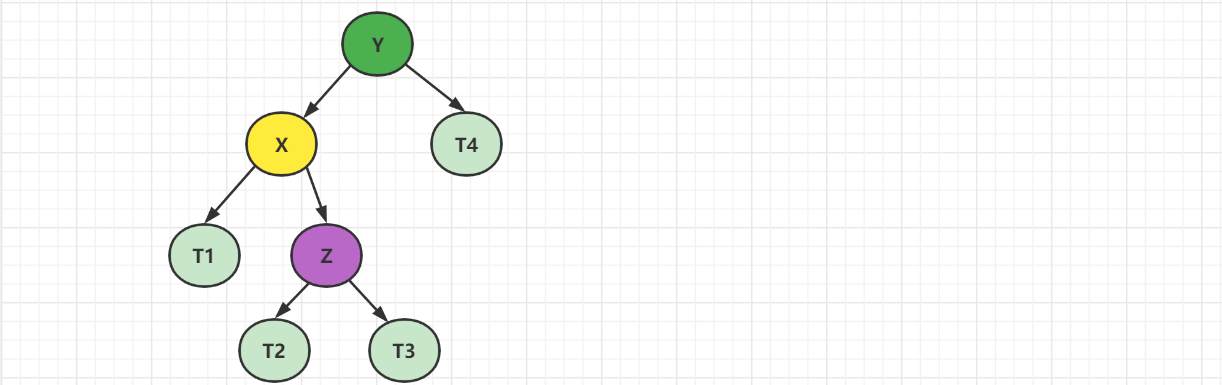
先对X进行左旋转,变成LL模式,然后继续右旋转
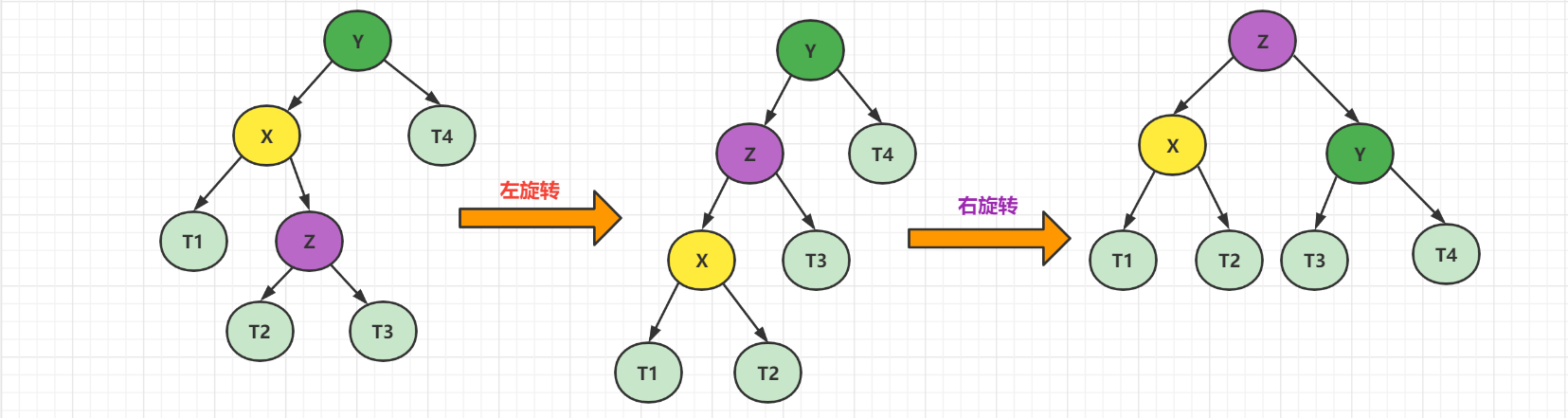
2、案例实现
对B做了一次逆时针旋转,对A做了一次顺时针旋转。( 先左后右)
1.5 RL平衡旋转
1、思路分析
插入的元素在不平衡的节点的右侧的左侧。
节点大小:T1 < Y < T2 < z < T3 < X < T4
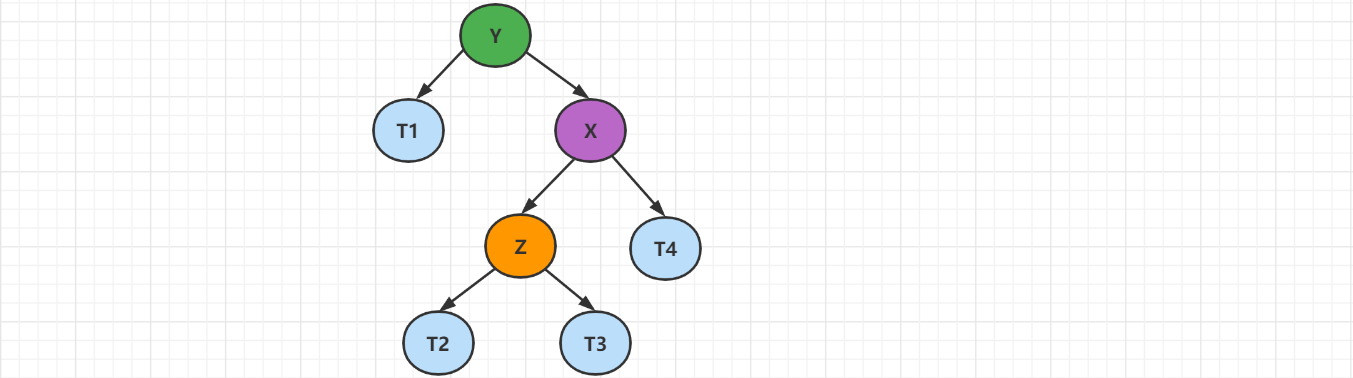
先对X进行右旋转,变成RR模式,然后继续左旋转
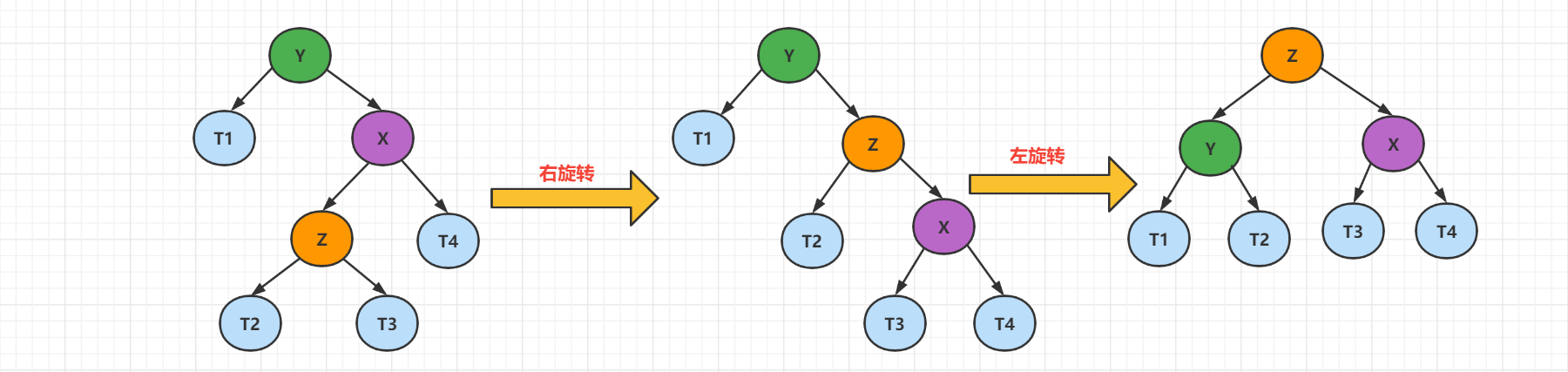
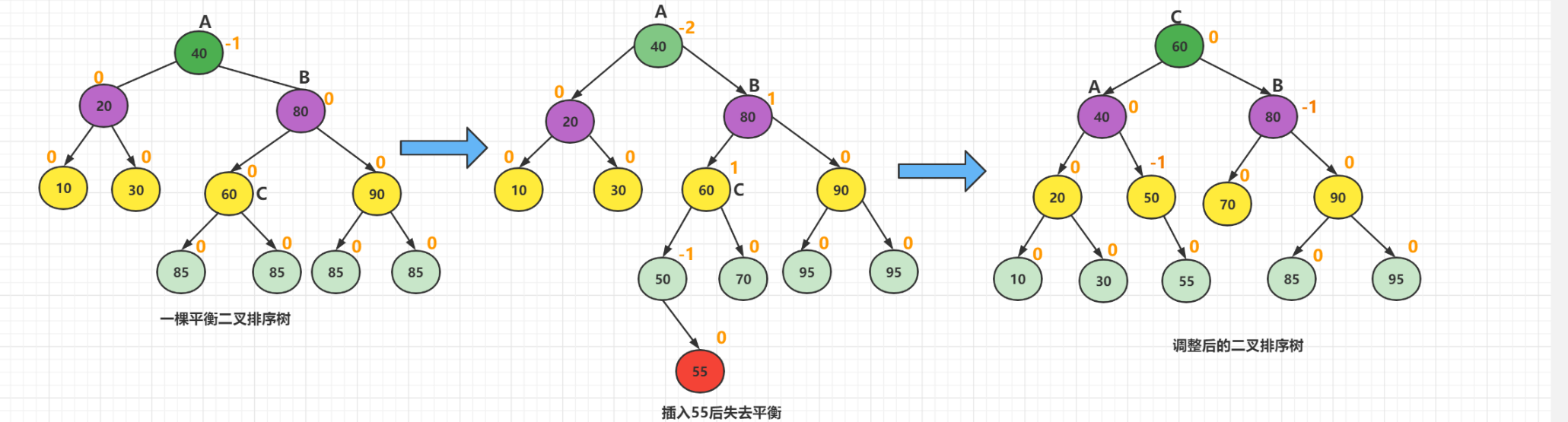
2、案例实现
对B做了一次顺时针旋转,对A做了 一次逆时针旋转。(先右后左)
1.6 代码实现
1、接口类:Map
package cn.alvtree.demo01;
// Map接口
public interface Map<K, V> {
void put(K key, V value);
V remove(K key);
boolean contains(K key);
V get(K key);
void update(K key, V value);
int size();
boolean isEmpty();
}
2、工具类:FileOperation
package cn.alvtree.demo01;
import java.io.BufferedInputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Locale;
import java.util.Scanner;
// 文件相关操作
public class FileOperation {
// 读取文件名称为filename中的内容,并将其中包含的所有词语放进words中
public static boolean readFile(String filename, ArrayList<String> words){
if (filename == null || words == null){
System.out.println("filename is null or words is null");
return false;
}
// 文件读取
Scanner scanner;
try {
File file = new File(filename);
if(file.exists()){
FileInputStream fis = new FileInputStream(file);
scanner = new Scanner(new BufferedInputStream(fis), "UTF-8");
scanner.useLocale(Locale.ENGLISH);
}
else
return false;
}
catch(IOException ioe){
System.out.println("Cannot open " + filename);
return false;
}
// 简单分词
// 这个分词方式相对简陋, 没有考虑很多文本处理中的特殊问题
// 在这里只做demo展示用
if (scanner.hasNextLine()) {
String contents = scanner.useDelimiter("\\A").next();
int start = firstCharacterIndex(contents, 0);
for (int i = start + 1; i <= contents.length(); )
if (i == contents.length() || !Character.isLetter(contents.charAt(i))) {
String word = contents.substring(start, i).toLowerCase();
words.add(word);
start = firstCharacterIndex(contents, i);
i = start + 1;
} else
i++;
}
return true;
}
// 寻找字符串s中,从start的位置开始的第一个字母字符的位置
private static int firstCharacterIndex(String s, int start){
for( int i = start ; i < s.length() ; i ++ )
if( Character.isLetter(s.charAt(i)) )
return i;
return s.length();
}
}
3、ALV实现类:AVLTree
package cn.alvtree.demo01;
import cn.map.demo.Map;
import java.util.ArrayList;
/***
* 二叉平衡树实现
* @param <K>
* @param <V>
*/
public class AVLTree<K extends Comparable<K>,V> implements Map<K, V> {
// 创建Node节点
private class Node {
public K key;
public V value;
// 左右指针域
public Node left, right;
// 当前节点所处的高度,默认为1
public int height;
// 构造方法
public Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
@Override
public String toString() {
return "(" + key +"," +value + ")";
}
}
// 二分搜索树的根节点的指针
private Node root;
// 二分搜索树的元素的个数
private int size;
// TreeMap初始化
public AVLTree(){
root = null;
size = 0;
}
/***
* 返回以node为根节点的二分搜索树中,key所在的节点
* @param node
* @param key
* @return
*/
private Node getNode(Node node, K key){
if(node == null){
return null;
}
if(key.equals(node.key)){
return node;
}else if(key.compareTo(node.key) < 0){
return getNode(node.left, key);
}else {
return getNode(node.right, key);
}
}
/***
* 获得节点Node的高度,如果节点为空,则高度为0
* @param node
* @return
*/
private int getHeight(Node node){
if(node == null){
return 0;
}
return node.height;
}
/***
* 获得节点node的平衡因子
* 计算平衡因子:左子树的高度-右子树的高度
* > 0 左边比右边高
* == 0 左右一样高
* < 0 右边比左边高
* @param node
* @return
*/
private int getBalanceFactor(Node node) {
if(node == null){
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
/***
* 判断该二叉树是不是二分搜索树
* @return
*/
public boolean isBinarySearchTree(){
// 将Map中的key值存放在List中
ArrayList<K> keys = new ArrayList<>();
// 使用中序遍历,遍历的结果都是有序的
inOrder(root, keys);
// 判断该数组是否升序
for (int i=1; i < keys.size(); i++){
if(keys.get(i-1).compareTo(keys.get(i)) > 0){
return false;
}
}
return true;
}
// 中序遍历
private void inOrder(Node node, ArrayList<K> keys) {
if(node == null){
return;
}
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
/***
* 判断该二叉树是否是一棵平衡二叉树
* @return
*/
public boolean isBalanced(){
return isBalanced(root);
}
/***
* 判断以Node为根的二叉树是否是一棵平衡二叉树
* @return
*/
private boolean isBalanced(Node node){
if(node == null){
return true;
}
// 拿到平衡因子
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1){
return false;
}
// 判断当前结点的左右子树是否是平衡二叉树
return isBalanced(node.left) && isBalanced(node.right);
}
/***
* 对节点y进行向右旋转操作,返回旋转后新的根节点x
* @param y
* @return
*/
private Node rightRotate(Node y){
Node x = y.left;
Node T3 = x.right;
// 向右旋转的过程【LL平衡旋转】
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right) + 1);
x.height = Math.max(getHeight(x.left), getHeight(x.right) + 1);
// 返回该节点
return x;
}
/***
* 对节点y进行向左旋转操作,返回旋转后新的根节点x
* @param y
* @return
*/
private Node leftRotate(Node y){
Node x = y.right;
Node T2 = x.left;
// 向右旋转的过程【LL平衡旋转】
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right) + 1);
x.height = Math.max(getHeight(x.left), getHeight(x.right) + 1);
// 返回该节点
return x;
}
/***
* 向TreeMap添加新的元素(key, value)
* @param key
* @param value
*/
@Override
public void put(K key, V value) {
root = put(root, key, value);
}
/***
* 向以node为根的AVLTree中插入元素(key, value),递归算法
* 返回插入新节点后AVLTree的根
* @param node
* @param key
* @param value
* @return
*/
private Node put(Node node, K key, V value) {
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0){
// 以node左子树为根节点,再添加一个元素
node.left = put(node.left, key, value);
}else if(key.compareTo(node.key) > 0){
// 以node右子树为根节点,再添加一个元素
node.right = put(node.right, key, value);
}else {
// 当key相等时,value直接覆盖
node.value = value;
}
// 更新节点的高度
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// 左侧的左侧不平衡【右旋转LL】
if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0){
return rightRotate(node);
}
// 左侧的右侧不平衡【先左后右旋转LR】
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
// 当前节点的左孩子进行一次左旋转
node.left = leftRotate(node.left);
return rightRotate(node);
}
// 右侧的右侧不平衡【左旋转RR】
if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0){
return leftRotate(node);
}
// 右侧的左侧不平衡【先右后左旋转RL】
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
/***
* 判断TreeMap中是否包含元素e
* @param key
* @return
*/
@Override
public boolean contains(K key) {
return getNode(root, key) != null;
}
/***
* 通过键获取值
* @param key
* @return
*/
@Override
public V get(K key) {
Node node = getNode(root, key);
return node == null ? null: node.value;
}
/***
* 通过key,修改值
* @param key
* @param value
*/
@Override
public void update(K key, V value) {
Node node = getNode(root, key);
if(node == null){
throw new IllegalArgumentException(key + "update key out of bounds");
}
node.value = value;
}
/***
* 获取TreeMap的元素个数
* @return
*/
@Override
public int size() {
return size;
}
/***
* 判断TreeMap是否为空
* @return
*/
@Override
public boolean isEmpty() {
return size == 0 && root == null;
}
/***
* 返回以node为根的二分搜索树的最小值所在的节点
* @param node
* @return
*/
private Node minimum(Node node){
if(node.left == null){
return node;
}
return minimum(node.left);
}
/***
* 从二分搜索树中删除键为key的节点
* @param key
* @return
*/
@Override
public V remove(K key) {
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
/***
* 删除掉以node为根的AVLTree的元素(key, value),递归算法
* 返回删除节点后新的AVLTree的根
* @param node
* @param key
* @return
*/
private Node remove(Node node, K key) {
if (node == null) {
return null;
}
// 创建最终要返回的node
Node retNode;
if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
retNode = node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
retNode = node;
} else {// e.compareTo(node.e) == 0
// 如果左子树为空
if(node.left == null){
Node rightNode = node.right;
// 置空操作
node.right = null;
size --;
retNode = rightNode;
// 待删除节点右子树为空的情况
}else if(node.right == null){
Node leftNode = node.left;
// 置空操作
node.left = null;
size --;
retNode = leftNode;
}else{
// 待删除节点左右子树均不为空的情况,找到node结点的后继
Node successor = minimum(node.right);
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
successor.right = remove(node.right, successor.key);
// 用这个节点顶替待删除节点的位置
successor.left = node.left;
// 置空操作
node.left = node.right = null;
retNode = successor;
}
}
// 当retNode为null
if(retNode == null){
return null;
}
// 更新节点的高度
retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(retNode);
// 左侧的左侧不平衡【右旋转LL】
if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0){
return rightRotate(retNode);
}
// 左侧的右侧不平衡【先左后右旋转LR】
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
// 当前节点的左孩子进行一次左旋转
node.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
// 右侧的右侧不平衡【左旋转RR】
if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){
return leftRotate(retNode);
}
// 右侧的左侧不平衡【先右后左旋转RL】
if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}
}
4、测试结果
测试类:AVLTreeDemo
package cn.alvtree.demo01;
import java.util.ArrayList;
public class AVLTreeDemo {
public static void main(String[] args) {
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("src/pride-and-prejudice.txt", words)) {
// 创建map对象
AVLTree<String, Integer> map = new AVLTree<>();
for (String word : words) {
if (map.contains(word))
map.update(word, map.get(word) + 1);
else
map.put(word, 1);
}
System.out.println("总单词个数: " + map.size());
System.out.println("是否是二分搜索树:" + map.isBinarySearchTree());
System.out.println("是否是平衡树(ALV): " + map.isBalanced());
// 删除元素
for (String word : words){
map.remove(word);
if(!map.isBinarySearchTree() || !map.isBalanced()){
throw new RuntimeException("该树非BinarySearchTree OR AVLTree");
}
}
}
}
}
执行结果



 浙公网安备 33010602011771号
浙公网安备 33010602011771号