【论文笔记 - CycleGAN】Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks
CycleGAN:Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks——非配对的图像转译,论文发表于2017年的ICCV。
CycleGAN可以实现风格迁移功能,通过两个镜像对称的GAN构成一个环形网络。针对无配对数据,在源域和目标域之间不需要建立一对一的映射就可以实现风格迁移。
Resources and papers
Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks
CycleGAN implementation from scratch
Read-through
Abstract
For many tasks, paired training data will not be available. We present an approach for learning to translate an image from a source domain \(X\) to a target domain \(Y\) in the absence of paired examples.
很多任务中,配对的训练集是无法获得的。
Our goal is to learn a mapping \(G:X\rightarrow Y\) such that the distribution of images from \(G(X)\) is indistinguishable from the distribution \(Y\) using an adversarial loss. Because this mapping is highly under-constrained, we couple it with an inverse mapping \(F:Y\rightarrow X\) and introduce a cycle consistency loss to enforce \(F(G(X))\approx X\) (and vice versa).
GAN是非常的不可控制的(under-constrained),因此论文在网络中加入了循环一致性损失(cycle consistency loss),先通过第一个生成器 \(G\) 把 \(X\) 转成 \(Y\),然后再通过第二个生成器转回 \(X^{'}\),要求这个经过了两次转换的 \(X^{'}\) 和 \(X\) 接近。
Introduction
In this paper, we present a method that can learn to do the same: capturing special characteristics of one image collection and figuring out how these characteristics could be translated into the other image collection, all in the absence of any paired training examples.
尽管我们没有真正看过莫奈作画,但我们可以想象出他作画的场景。我们对于莫奈风景画的特征有着一定的知识储备,可以将他的作品和其他作品区分开,因此也就可以将一种绘画风格转换成另一种风格。
论文提出了一种让AI具有同样能力的算法,从一系列画作中提取风格,并学会如何将其转化成另一种风格,而这都是在没有成对的训练集的情况下完成的。
Years of research in computer vision, image processing, computational photography, and graphics have produced powerful translation systems in the supervised setting, where example image pairs \(\{x_i,y_i\}_{i=1}^N\) are available. However, obtaining paired training data can be difficult and expensive.
计算机视觉等研究发展这么多年,已经有很多基于监督学习(有标注)的图像迁移算法。但是配对数据集采集非常困难,只适用于个别场景,如航拍图转地图之类。而艺术风格转换、zebra2horse这些任务根本就不可能获得这样的数据。
We therefore seek an algorithm that can learn to translate between domains without paired input-output examples. We assume there is some underlying relationship between the domains.
Although we lack supervision in the form of paired examples, we can exploit supervision at the level of sets.
论文假设两个数据集在图像域的底层存在一定的关系,比如是在同一个底层场景渲染得到的。所以论文选择在数据集(图像域)而非数据(单个图像)的层次构建监督学习问题。
However, such a translation(指单纯把 \(X\) 转成 \(Y\)) does not guarantee that an individual input \(x\) and output \(y\) are paired up in a meaningful way – there are infinitely many mappings \(G\) that will induce the same distribution over \(\hat y\).
Moreover, in practice, we have found it difficult to optimize the adversarial objective in isolation: standard procedures often lead to the well-known problem of mode collapse, where all input images map to the same output image and the optimization fails to make progress.
单纯把 \(X\) 转成 \(Y\),虽然生成的 \(\hat y\) 可能很像 \(y\),但可能已经丢失了 \(x\) 原来的特征,所以CycleGAN需要再把 \(\hat y\) 转回 \(x\)。此外单纯使用GAN的损失函数(不引入循环一致性损失)还会造成模式崩溃(mode collapse)的问题——无论什么输入,都只会产生同样的输出。
Therefore, we exploit the property that translation should be “cycle consistent”. Mathematically, if we have a translator \(G:X\rightarrow Y\) and another translator \(F:Y\rightarrow X\), then \(G\) and \(F\) should be inverses of each other, and both mappings should be bijections. We apply this structural assumption by training both the mapping \(G\) and \(F\) simultaneously, and adding a cycle consistency loss that encourages \(F(G(x))\approx x\) and \(G(F(y))\approx y\). Combining this loss with adversarial losses on domains \(X\) and \(Y\) yields our full objective for unpaired image-to-image translation.
论文指出,图像迁移应当是“循环一致”的。从数学上来讲,两个映射 \(G\) 和 \(F\) 需要互逆且均为双射(模式崩溃就是多对一了)。论文引入了一种叫做“循环一致性损失”的损失函数,以使得 \(F(G(x))\) 与 \(x\) 尽可能接近,反之亦然
Related work
The idea of using transitivity as a way to regularize structured data has a long history.
Of these, Zhou et al. and Godard et al. are most similar to our work, as they use a cycle consistency loss as a way of using transitivity to supervise CNN training.
Cycle Consistency:使用传递性(transitivity)作为正则化结构化数据的方法已经有很长的历史了(比如GNN、图数据挖掘、隐马尔科夫链),以前也有论文将循环一致性损失用于监督式CNN训练中。
Neural Style Transfer is another way to perform image-to-image translation, which synthesizes a novel image by combining the content of one image with the style of another image (typically a painting) based on matching the Gram matrix statistics of pre-trained deep features. Our primary focus, on the other hand, is learning the mapping between two image collections, rather than between two specific images, by trying to capture correspondences between higher-level appearance structures.
神经风格迁移(Neural Style Transfer)是另外一种图像转图像的方法,把内容图和风格图一起输入,输出的则是一张既有内容,又有风格的图像。它实现的是单张图像的风格迁移,而CycleGAN做的则是两个图像域的风格迁移。而且不同于神经风格迁移求每一个像素的梯度,反复迭代使得生成的图像越来越符合最终的效果,而CycleGAN则是在图像层面的,不需要对像素进行优化。
 +
+ =
=
Formulation
Our objective contains two types of terms: adversarial losses for matching the distribution of generated images to the data distribution in the target domain; and cycle consistency losses to prevent the learned mappings \(G\) and \(F\) from contradicting each other.
Adversarial Loss
对于映射 \(G:X\rightarrow Y\),设计如下的损失函数:
双人极大极小零和博弈:\(\min_G\max_{D_Y}\mathcal{L}_{GAN}(G,D_Y,X,Y).\)
对于另一个映射 \(F:Y\rightarrow X\),损失函数类似:
双人极大极小零和博弈:\(\min_F\max_{D_X}\mathcal{L}_{GAN}(F,D_X,Y,X).\)
Cycle Consistency Loss
With large enough capacity, a network can map the same set of input images to any random permutation of images in the target domain, where any of the learned mappings can induce an output distribution that matches the target distribution. Thus, adversarial losses alone cannot guarantee that the learned function can map an individual input \(x_i\) to a desired output \(y_i\).
对抗损失本身无法保证学习到的映射函数可以准确地把 \(x_i\) 映射到想要的 \(y_i\) 上。
Cycle-consistency loss的作用有三个方面:
- 使得迁移过去的图像仍保留原始图像的信息
- 间接实现了pix2pix的paired image translation功能
- 防止模式崩溃
To further reduce the space of possible mapping functions, we argue that the learned mapping functions should be cycle-consistent: for each image \(x\) from domain \(X\), the image translation cycle should be able to bring \(x\) back to the original image, i.e., \(x\rightarrow G(x)\rightarrow F (G(x))\approx x\). We call this forward cycle consistency. Similarly, for each image \(y\) from domain \(Y\) , \(G\) and \(F\) should also satisfy backward cycle consistency: \(y\rightarrow F(y)\rightarrow G(F(y))\approx y\).

论文提出两个映射函数应当遵循循环一致性(cycle-consistency),包括正向循环一致性(forward cycle consistency)和反向循环一致性(backward cycle consistency)。CycleGAN通过一个循环一致性损失达到这一目标:
In preliminary experiments, we also tried replacing the L1 norm in this loss with an adversarial loss between \(F (G(x))\) and \(x\), and between \(G(F (y))\) and \(y\), but did not observe improved performance.
论文也尝试用一个GAN来判别究竟是循环生成的图像还是原来的图像,不过并没有观察到改进。
Full Objective
最终的目标函数是:
需要解决的问题是
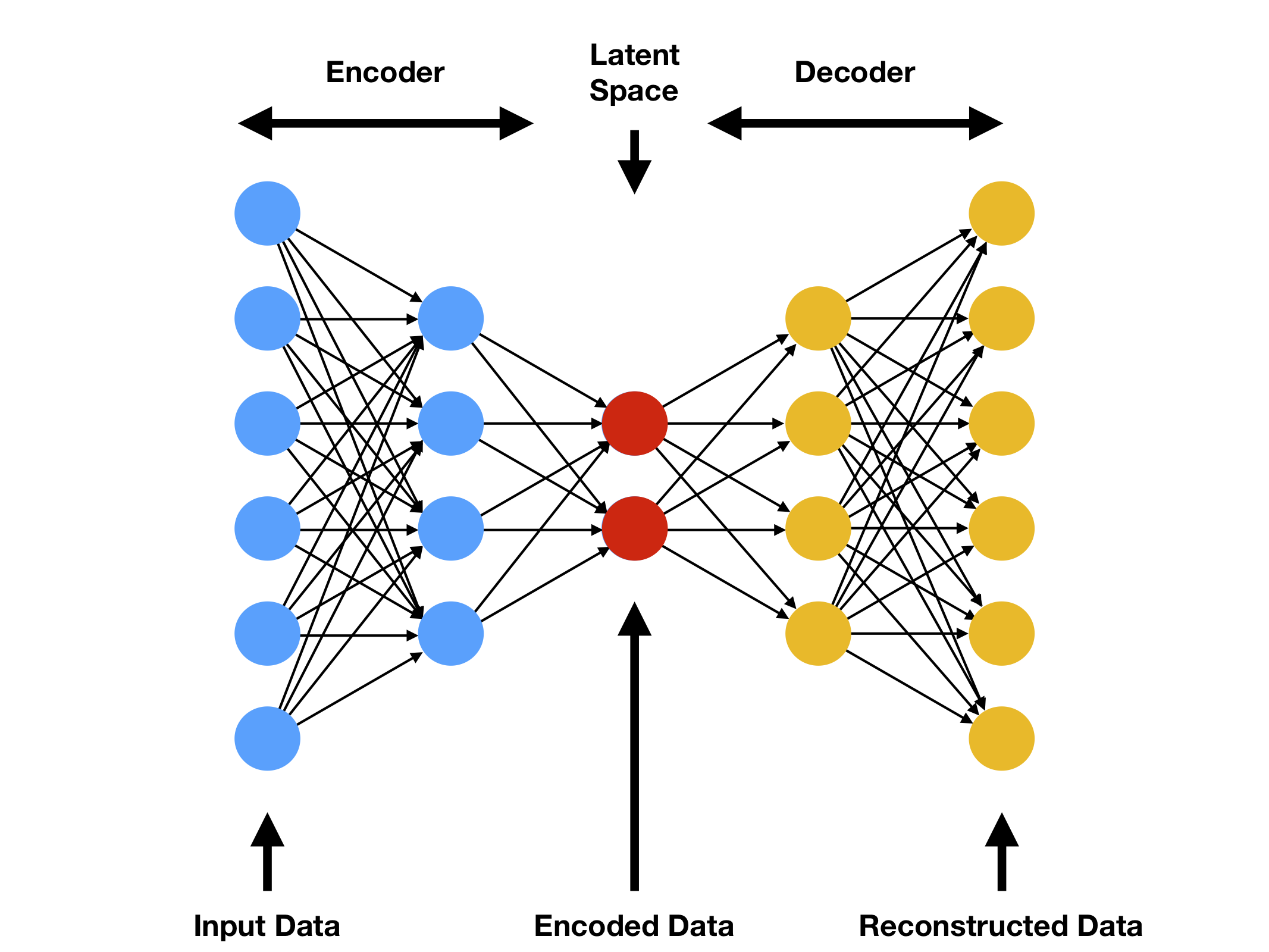
Notice that our model can be viewed as training two “autoencoders” : we learn one autoencoder \(F\circ G:X\rightarrow X\) jointly with another \(G\circ F:Y\rightarrow Y\) . However, these autoencoders each have special internal structures: they map an image to itself via an intermediate representation that is a translation of the image into another domain. Such a setup can also be seen as a special case of “adversarial autoencoders”, which use an adversarial loss to train the bottleneck layer of an autoencoder to match an arbitrary target distribution. In our case, the target distribution for the \(X\rightarrow X\) autoencoder is that of the domain \(Y\).
CycleGAN的模型可以被看成是两个自编码器,更确切地说是两个对抗自编码器(Adversial Autoencoder,AAE)。AAE是一种结合了自编码器和生成对抗网络的模型,与常规的自编码器不同,AAE加入了一个判别器,通过训练使得瓶颈层(bottleneck layer)处的分布和目标分布匹配,CycleGAN恰恰是AAE的一种特例。

Implementation
This network contains three convolutions, several residual blocks, two fractionally-strided convolutions with stride \(\frac12\), and one convolution that maps features to RGB. We use \(6\) blocks for \(128\times128\) images and \(9\) blocks for \(256\times256\) and higher-resolution training images. We use instance normalization. For the discriminator networks we use \(70\times70\) PatchGANs, which aim to classify whether $70\times70 $ overlapping image patches are real or fake.
-
三个卷积层,几个残差块,两个分数步长卷积,最后再来一次卷积
分数步长卷积:
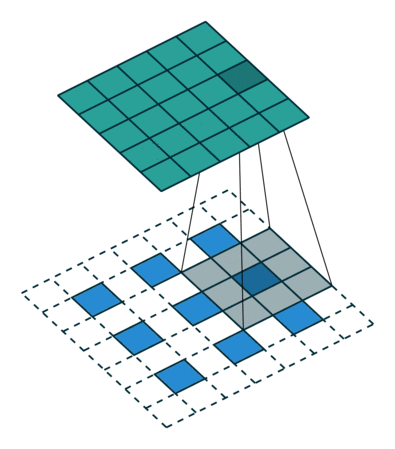
-
使用Instance Normalization
Instance Normalization和Batch Normalization是深度学习中常用的归一化技术,它们的主要区别在于应用的对象不同。
Batch Normalization(批归一化)是应用于批次中的每个数据样本上的归一化技术。在神经网络中,每个隐藏层的输入通常是一批数据样本。Batch Normalization通过对每个批次的样本进行均值和方差的归一化,使网络更容易收敛并提高了模型的泛化能力。
Instance Normalization(实例归一化)是应用于每个单独的数据样本的归一化技术。它主要用于图像处理中,对于每个图像的每个通道(RGB),计算通道内的均值和方差,然后将通道内的每个像素进行归一化,从而提高模型的鲁棒性和泛化能力。
因此,Instance Normalization和Batch Normalization的主要区别在于归一化的粒度不同:Instance Normalization是对单个样本进行归一化,而Batch Normalization是对整个批次的样本进行归一化。此外,Instance Normalization通常用于图像处理中,而Batch Normalization则广泛应用于各种深度学习任务中。
——ChatGPT
-
判别器中依旧使用 \(70\times70\) 的PatchGAN
For \(\mathcal{L}_{GAN}\), we replace the negative log likelihood objective by a least-squares loss. This loss is more stable during training and generates higher quality results. In particular, for a GAN loss \(\mathcal{L}_{GAN}(G,D,X,Y)\), we train the \(G\) to minimize \(\mathbb{E}_{x\sim p_{\mathrm{data}}(x)}[(D(G(x))-1)^2]\) and train the \(D\) to minimize \(\mathbb{E}_{ y\sim p_{\mathrm{data}}(y)}[(D(y)-1)^2]+\mathbb{E}_{ x\sim p_{\mathrm{data}}(x)}[D(G(x))^2]\).
CycleGAN将adversarial loss中的损失函数换成了最小二乘损失函数(L2范数,BCE->MSE),这样训练更加稳定。
To reduce model oscillation, we update the discriminators using a history of generated images rather than the ones produced by the latest generators. We keep an image buffer that stores the \(50\) previously created images.
为了避免振荡(oscillation),论文中使用缓存中的文件来训练。
For all the experiments, we set \(\lambda=10\). We use the Adam solver with a batch size of \(1\). All networks were trained from scratch with a learning rate of \(0.0002\). We keep the same learning rate for the first 100 epochs and linearly decay the rate to zero over the next 100 epochs.
- 循环一致性损失的系数 \(\lambda\) 设置为 \(10\)
- Adam学习率 \(2\times10^{-4}\)
Result
Evaluation
与先前的pix2pix一样,CycleGAN同样使用了AMT众包平台和FCN-score。
We also compare against pix2pix, which is trained on paired data, to see how close we can get to this “upper bound” without using any paired data.
Baselines中有一个是pix2pix,对于有成对的数据集用于训练的任务,pix2pix用来表征CycleGAN可以达到的上界。
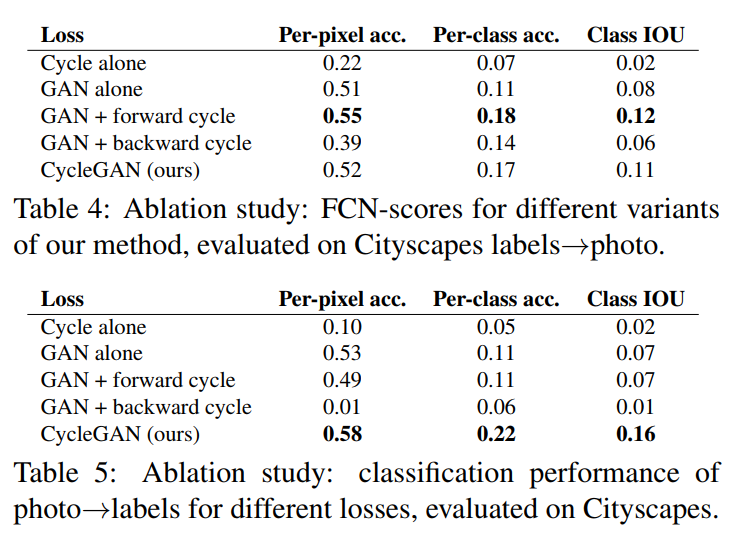

We compare against ablations of our full loss. Removing the GAN loss substantially degrades results, as does removing the cycle-consistency loss. We therefore conclude that both terms are critical to our results. We also evaluate our method with the cycle loss in only one direction: GAN + forward cycle loss \(\mathbb{E}_{x\sim p_{\mathrm{data}}(x)}[\|F(G(x))-x\|_1]\), or GAN + backward cycle loss \(\mathbb{E}_{y\sim p_{\mathrm{data}}(y)}[\|G(F(y))-y\|_1]\) and find that it often incurs training instability and causes mode collapse, especially for the direction of the mapping that was removed.
论文分别移除了部分损失函数作为比较,发现两个损失函数都是必要的,而且对于循环一致性损失来说,如果只用一半,经常会造成训练的不稳定以及导致模式崩溃的问题。
| Cycle alone | GAN alone | GAN+forward | GAN+backward | CycleGAN |
|---|---|---|---|---|
| 迁移失败 | 模式崩溃 | 模式崩溃 | 模式崩溃+迁移失败 | 效果不错 |
The image quality of our results is close to those produced by the fully supervised pix2pix while our method learns the mapping without paired supervision.
归功于循环一致性损失,对于那些有配对数据集的任务,CycleGAN的表现和pix2pix一样好。
Applications
For painting\(\rightarrow\)photo, we find that it is helpful to introduce an additional loss to encourage the mapping to preserve color composition between the input and output. In particular, we adopt the technique of Taigman et al. and regularize the generator to be near an identity mapping when real samples of the target domain are provided as the input to the generator: i.e., \(\mathcal{L}_{identity}(G,F)=\mathbb{E}_{y\sim p_{\mathrm{data}}(y)}[\|G(y) - y\|_1]+\mathbb{E}_{x\sim p_{\mathrm{data}}(x)}[\|F(x) - x\|_1]\).

Without \(\mathcal{L}_{identity}\), the generator \(G\) and \(F\) are free to change the tint of input images when there is no need to. For example, when learning the mapping between Monet’s paintings and Flickr photographs, the generator often maps paintings of daytime to photographs taken during sunset, because such a mapping may be equally valid under the adversarial loss and cycle consistency loss. The effect of this identity mapping loss are shown in the figure above.
油画转真实照片的时候,颜色上会出现不真实的情况。这是因为CycleGAN的目标是只要能骗过判别器就行,所以是不用关注颜色的。识别损失函数(Identity Loss)的目标是最小化源域图像和生成图像之间的差异,它能够一定程度上保留源域图像中的风格信息。
但是这有可能导致生成器过度关注源域图像中的风格信息,而忽略了目标域图像的内容,从而影响生成器的图像质量。而且添加识别损失函数也会增加训练的复杂度和训练难度,需要花费更多的时间和计算资源来训练模型,可能会导致模型训练的不稳定和过拟合等问题。
Limitations and Discussion

Although our method can achieve compelling results in many cases, the results are far from uniformly positive. On translation tasks that involve color and texture changes, as many of those reported above, the method often succeeds. We have also explored tasks that require geometric changes, with little success. This failure might be caused by our generator architectures which are tailored for good performance on the appearance changes. Handling more varied and extreme transformations, especially geometric changes, is an important problem for future work.
CycleGAN擅长改变颜色和纹理,不擅长改变几何形状,例如斑马与马转换的时候,CycleGAN不会把斑马的鬃毛和马的鬃毛进行转换。这是因为CycleGAN没有理解图像中的高级语义,没有先验知识和三维信息。CycleGAN也没有条件输入信息,没有区分开前景与背景。
Some failure cases are caused by the distribution characteristics of the training datasets. For example, our method has got confused in the horse\(\rightarrow\)zebra example, because our model was trained on the wild horse and zebra synsets of ImageNet, which does not contain images of a person riding a horse or zebra.
此外对于经典的普京骑马的图,CycleGAN出错的原因在于训练集和测试集分布不一致。
Resolving this ambiguity may require some form of weak semantic supervision. Integrating weak or semi-supervised data may lead to substantially more powerful translators, still at a fraction of the annotation cost of the fully-supervised systems.
要解决一系列的问题,需要引入先验知识,比如弱监督或半监督的标签,告诉CycleGAN一些图像并不会体现出来的知识。我们距离这样的目标还差得很远,甚至可能无法实现。
Nonetheless, in many cases completely unpaired data is plentifully available and should be made use of. This paper pushes the boundaries of what is possible in this “unsupervised” setting.
不管怎样,数据集不配对的任务占绝大多数(除了图像处理外,还包括非配对文本风格迁移,语音识别等),CycleGAN总的来说还是为这一部分任务开拓了一种新的思路。
Implementation
Let c7s1-k denote a \(7\times7\) Convolution-InstanceNormReLU layer with \(k\) filters and stride \(1\). dk denotes a \(3\times 3\) Convolution-InstanceNorm-ReLU layer with \(k\) filters and stride \(2\). Reflection padding was used to reduce artifacts. Rk denotes a residual block that contains two \(3\times 3\) convolutional layers with the same number of filters on both layer. uk denotes a \(3\times3\) fractional-strided-ConvolutionInstanceNorm-ReLU layer with \(k\) filters and stride \(\frac12\).
Generator
class ConvBlock(nn.Module):
def __init__(self, in_channels, out_channels, down=True, use_act=True, **kwargs):
super().__init__()
self.conv = nn.Sequential(
nn.Conv2d(in_channels, out_channels, padding_mode="reflect", **kwargs) if down else
nn.ConvTranspose2d(in_channels, out_channels, **kwargs),
nn.InstanceNorm2d(out_channels),
nn.ReLU(inplace=True) if use_act else nn.Identity()
)
def forward(self, x):
return self.conv(x)
class ResidualBlock(nn.Module):
def __init__(self, channels):
super().__init__()
self.block = nn.Sequential(
ConvBlock(channels, channels, kernel_size=3, padding=1),
ConvBlock(channels, channels, use_act=False, kernel_size=3, padding=1)
)
def forward(self, x):
return x + self.block(x)
The network with 6 residual blocks consists of:
c7s1-64,d128,d256,R256,R256,R256,R256,R256,R256,u128,u64,c7s1-3
The network with 9 residual blocks consists of:
c7s1-64,d128,d256,R256,R256,R256,R256,R256,R256,R256,R256,R256,u128,u64,c7s1-3
class Generator(nn.Module):
def __init__(self, img_channels, num_features=64, num_residuals=9):
super().__init__()
self.initial = nn.Conv2d(img_channels, num_features, kernel_size=7, stride=1, padding=3, padding_mode="reflect")
self.down_blocks = nn.ModuleList(
[
ConvBlock(num_features, num_features * 2, kernel_size=3, stride=2, padding=1),
ConvBlock(num_features * 2, num_features * 4, kernel_size=3, stride=2, padding=1)
]
)
self.res_blocks = nn.Sequential(
*[ResidualBlock(num_features * 4) for _ in range(num_residuals)]
)
self.up_blocks = nn.ModuleList(
[
ConvBlock(num_features * 4, num_features * 2, down=False, kernel_size=3, stride=2, padding=1, output_padding=1),
ConvBlock(num_features * 2, num_features, down=False, kernel_size=3, stride=2, padding=1, output_padding=1)
]
)
self.last = nn.Conv2d(num_features, img_channels, kernel_size=7, stride=1, padding=3, padding_mode="reflect")
def forward(self, x):
x = self.initial(x)
for layer in self.down_blocks:
x = layer(x)
x = self.res_blocks(x)
for layer in self.up_blocks:
x = layer(x)
return torch.tanh(self.last(x))
Discriminator
class Block(nn.Module):
def __init__(self, in_channels, out_channels, stride):
super().__init__()
self.conv = nn.Sequential(
nn.Conv2d(in_channels, out_channels, 4, stride, 1, bias=True, padding_mode="reflect"),
nn.InstanceNorm2d(out_channels),
nn.LeakyReLU(0.2)
)
def forward(self, x):
return self.conv(x)
70 × 70 discriminator architecture:
C64-C128-C256-C512
After the last layer, we apply a convolution to produce a 1-dimensional output. We do not use InstanceNorm for the first C64 layer. As an exception to the above notation, BatchNorm is not applied to the first C64 layer. We use leaky ReLUs with a slope of 0.2.
class Discriminator(nn.Module):
def __init__(self, in_channels=3, features=None):
super().__init__()
if features is None:
features = [64, 128, 256, 512]
self.initial = nn.Sequential(
nn.Conv2d(in_channels, features[0], kernel_size=4, stride=2, padding=1, padding_mode="reflect"),
nn.LeakyReLU(0.2)
)
layers = []
in_channels = features[0]
for feature in features[1:]:
layers.append(Block(in_channels, feature, stride=1 if feature == features[-1] else 2))
in_channels = feature
self.model = nn.Sequential(*layers)
self.final = nn.Sequential(
nn.Conv2d(in_channels, 1, kernel_size=4, stride=1, padding=1, padding_mode="reflect"),
nn.Sigmoid()
)
def forward(self, x):
x = self.initial(x)
x = self.model(x)
return self.final(x)
Train
# DEVICE = "cuda" if torch.cuda.is_available() else "cpu"
# LAMBDA_CYCLE = 10
# LAMBDA_IDENTITY = 0.0
def train_fn(disc_h, disc_z, gen_z, gen_h, loader, opt_disc, opt_gen, l1, mse, d_scaler, g_scaler):
loop = tqdm(loader, leave=True)
for idx, (zebra, horse) in enumerate(loop):
zebra = zebra.to(config.DEVICE)
horse = horse.to(config.DEVICE)
# Train Discriminators H and Z
with torch.cuda.amp.autocast():
fake_horse = gen_h(zebra)
d_h_real = disc_h(horse)
d_h_fake = disc_h(fake_horse.detach())
d_h_real_loss = mse(d_h_real, torch.ones_like(d_h_real))
d_h_fake_loss = mse(d_h_fake, torch.zeros_like(d_h_fake))
d_h_loss = d_h_real_loss + d_h_fake_loss
fake_zebra = gen_z(horse)
d_z_real = disc_z(zebra)
d_z_fake = disc_z(fake_zebra.detach())
d_z_real_loss = mse(d_z_real, torch.ones_like(d_z_real))
d_z_fake_loss = mse(d_z_fake, torch.zeros_like(d_z_fake))
d_z_loss = d_z_real_loss + d_z_fake_loss
# put it together
d_loss = (d_h_loss + d_z_loss) / 2
opt_disc.zero_grad()
d_scaler.scale(d_loss).backward()
d_scaler.step(opt_disc)
d_scaler.update()
# Train Generators H and Z
with torch.cuda.amp.autocast():
# adversarial loss for both generators
d_h_fake = disc_h(fake_horse)
d_z_fake = disc_z(fake_zebra)
loss_g_h = mse(d_h_fake, torch.ones_like(d_h_fake))
loss_g_z = mse(d_z_fake, torch.ones_like(d_z_fake))
# cycle loss
cycle_zebra = gen_z(fake_horse)
cycle_horse = gen_h(fake_zebra)
cycle_zebra_loss = l1(zebra, cycle_zebra)
cycle_horse_loss = l1(horse, cycle_horse)
# identity loss
identity_zebra = gen_z(zebra)
identity_horse = gen_h(horse)
identity_zebra_loss = l1(zebra, identity_zebra)
identity_horse_loss = l1(horse, identity_horse)
# add all together
g_loss = (
loss_g_z
+ loss_g_h
+ cycle_zebra_loss * config.LAMBDA_CYCLE
+ cycle_horse_loss * config.LAMBDA_CYCLE
+ identity_horse_loss * config.LAMBDA_IDENTITY
+ identity_zebra_loss * config.LAMBDA_IDENTITY
)
opt_gen.zero_grad()
g_scaler.scale(g_loss).backward()
g_scaler.step(opt_gen)
g_scaler.update()
Datasets
CycleGAN
Kaggle: link.
其中Horse<->Zebra的预训练权重:link

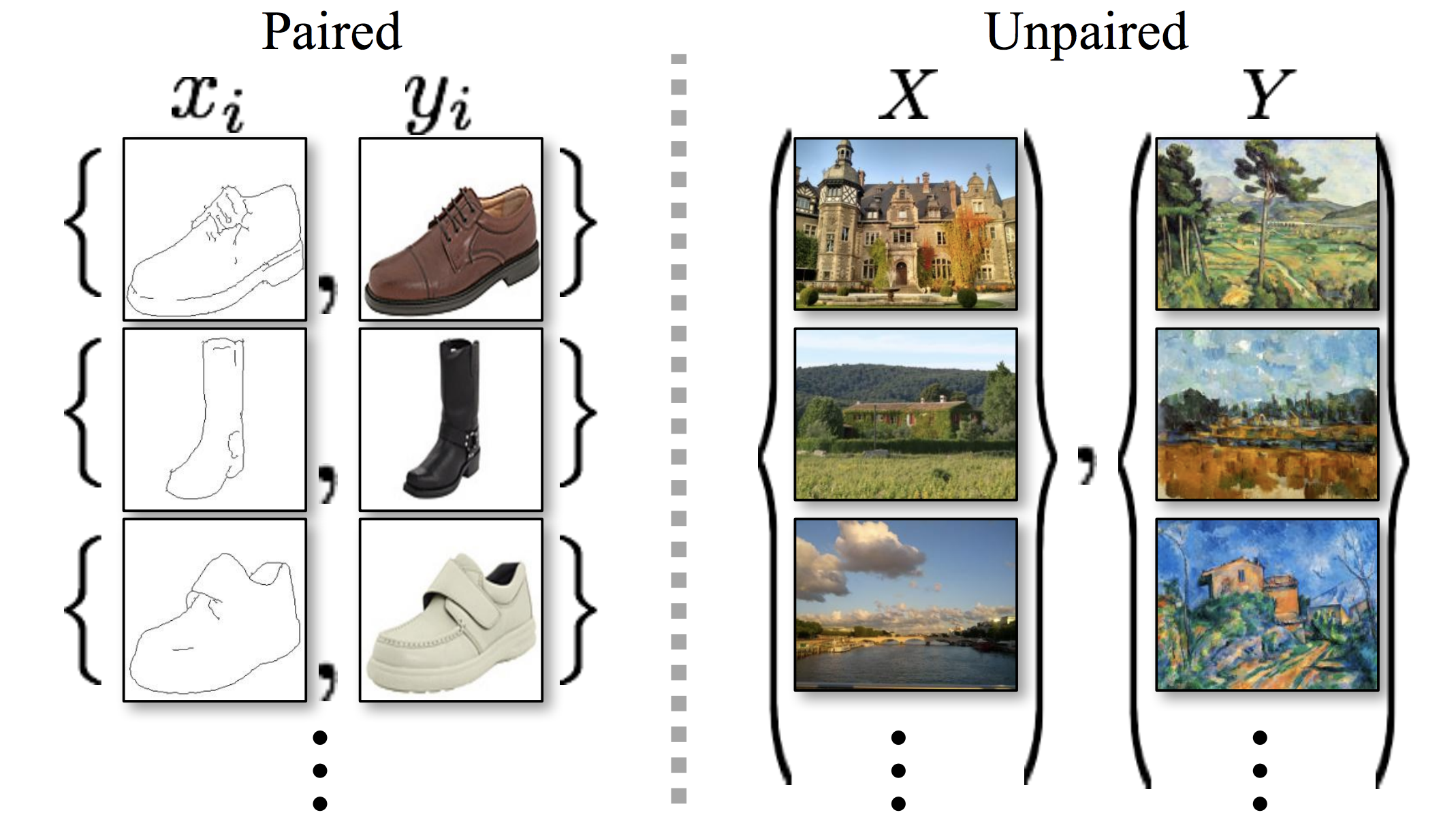 CycleGan可以实现风格迁移功能,通过两个镜像对称的GAN构成一个环形网络。针对无配对数据,在源域和目标域之间不需要建立一对一的映射就可以实现风格迁移。
CycleGan可以实现风格迁移功能,通过两个镜像对称的GAN构成一个环形网络。针对无配对数据,在源域和目标域之间不需要建立一对一的映射就可以实现风格迁移。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号