2020-王谱三套卷-数学一

2020-王谱3-1

T₂ 可以画图解决，\(\displaystyle N=a^2\max_{0<x<a}\{|f^{'}(x)|\}\Rightarrow |f^{'}(x)|\leqslant\dfrac N{a^2}\)，故 \(f(x)\) 图像夹在两直线之间，\(M\leqslant\dfrac N2\)

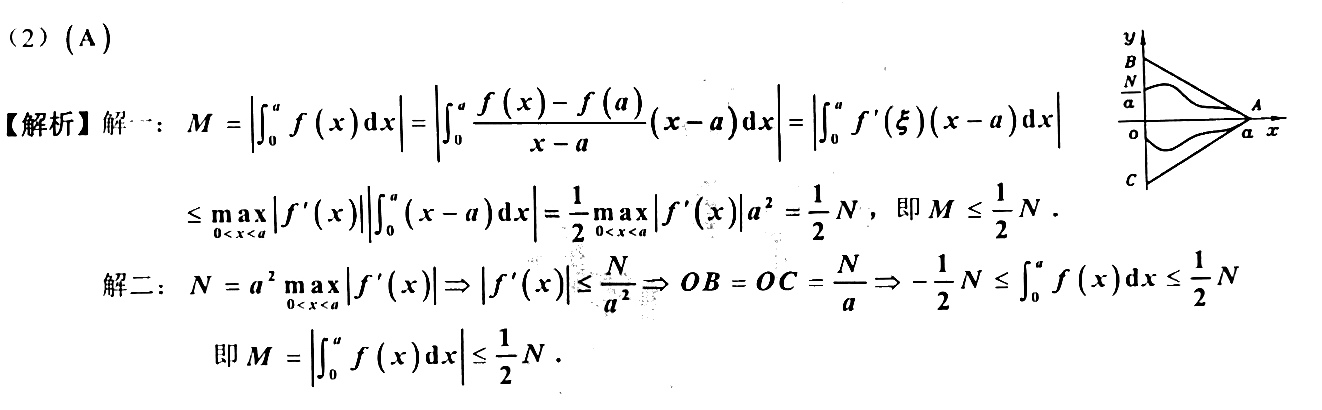
T₇ \(F(n_1,\,n_2)\) 与 \(\dfrac1{F(n_2,\,n_1)}\) 同分布，如这里的 \(Y\) 和 \(\dfrac1Y\) 同分布

• 关于上分位数：\(F\) 分布 \(F_{1-\alpha}(n_1,\,n_2)=\dfrac1{F_\alpha(n_2,\,n_1)}\)；\(t\) 分布 \(t_{1-\alpha}(n)=-t_\alpha(n),\,t^2_{\frac\alpha2}(n)=F_\alpha(1,\,n)\)

T₁₁ 奇谐函数偶次分量为 \(0\)，偶谐函数奇次分量为 \(0\)

T₁₄ \(f(x,\,y)\) 可以拆成 \(f_X(x)f_Y(y)\)，说明 \(X,\,Y\) 独立

T₁₅ 这道题没说可导，最好还是积分上去罢。本题 \(f(x)\) 原函数 \(F(x)\) 用分部，化简后还需要再往上积一次

T₁₉ 第一类曲面积分有的 \(\Sigma\) 本身就是一个圆（如平面切球体），有的投影 \(D_{xy}\) 才是一个圆（如平面切柱体），注意别搞错了

T₂₃ 细节：

• 关于大小写问题：
  • 最大似然函数 \(L\) 中，\(x_i\) 用小写；
  • 令 \(\dfrac{\mathrm{d}\ln L(\theta)}{\mathrm{d}\theta}=0\) 得到的 \(\displaystyle\theta=\dfrac1n\sum_{i=1}^nx_i\) 中，\(x_i\) 用小写；
  • 最后得出结论 \(\displaystyle\therefore\hat{\theta}=\dfrac1n\sum_{i=1}^nX_i\) 中，\(X_i\) 用大写
• 问 \(n\rightarrow\infty\) 时，\(\hat\theta\)（本题即 \(\overline{X}\)）近似服从什么分布，标准步骤：
  • \(\mu=EX=\theta,\,\sigma^2=DX=\theta^2\)，由列维-林德伯格中心极限定理，\(\displaystyle\lim_{n\rightarrow\infty}P\left\{\dfrac{\displaystyle\sum_{i=0}^nX_i-n\mu}{\sqrt{n}\sigma}\leqslant x\right\}=\Phi(x)\)
  • 即 \(\displaystyle\lim_{n\rightarrow\infty}P\left\{\dfrac{\dfrac1n\displaystyle\sum_{i=0}^nX_i-\theta}{\sqrt{\dfrac{\theta^2}{n}}}\leqslant x\right\}=\Phi(x)\)，即 \(\dfrac{\hat\theta-\theta}{\sqrt{\dfrac{\theta^2}{n}}}\) 近似服从 \(N(0,\,1)\) 分布，即 \(\hat\theta\) 近似服从 \(N(\theta,\,\dfrac{\theta^2}{n})\) 分布

2020-王谱3-2

T₇ 有放回的抽签问题，每一次抽签的分布都相同，本题计算期望只用 \(3\times一次的期望\) 即可

T₁₆ 二元函数只有一个变量真正在变化，可对其求偏导构造出偏微分

T₁₈ 涉及积分的题目，感觉经常有 \(\displaystyle\int_0^x(t-x)f(t)\,\mathrm{d}t\) 类型的构造，还不太熟悉。。

T₁₉ 顺便复习一下曲面积分的参数方程做法，感觉和雅可比其实是一样的

T₂₂ 感觉还是按 \(X\) 竖 \(Y\) 横来画表

2020-王谱3-3

T₁₀ 先将 \(f(x)=\dfrac{\sin x}x\) 展开再求导；\(x-\dfrac {x^3}3+\dfrac{x^5}5-\cdots=\arctan x\)

T₁₁ 注意曲线/曲面，球面/球体，注意积分区域

T₁₆ 已知 \(f(u,\,v)\)，求 \(w=f(x+y,\,x-y)\) 全微分：先对 \(u,\,v\) 全微分后，\(\mathrm{d}u=\mathrm{d}x+\mathrm{d}y,\,\mathrm{d}v=\mathrm{d}x-\mathrm{d}y\)

T₂₂ \(X,\,Y\) 独立，只要满足 \(F(x,\,y)=F_X(x)\cdot F_Y(y)\) 或 \(f(x,\,y)=f_X(x)\cdot f_Y(y)\) 即可直接得出结论