sdnu 1334 Jason's Water Problem【计算几何-多边形面积的计算】【负数取模】

1334.Jason's Water Problem

Time Limit: 1000 MS    Memory Limit: 32768 KB
Total Submission(s): 128    Accepted Submission(s): 23

Description

Calculus is the first lesson Jason had. It is tedious, so an interesting idea occurred to Jason. He took out his mobile phone and open the HDUOJ and found a water problem. He said to himself, “I must solve this f**king easy water problem in ten minutes! ”.

You were invited to compete with him online. Don’t be defeated.

Input

Multiple test cases, Each test first contains an integer N(3<=N<=100000) indicating the number of vertices of the polygon. The i-th of the following Nlines contains two integers xi and yi (0<=xi,yi<=10^9) separated by a blank. (xi,yi) is the i-th vertex of the polygon, and (x1,y1),...,(xn,yn) will be in counterclockwise order.

Output

For each test case, output a number as the answer which is the area of the polygon be multiplied by 2. In case the answer is greater than 1000000006, please modulo the answer with 1000000007.

Sample Input

3
0 0
1 0
0 1
4
0 0
1 0
1 1
0 1

Sample Output

1
2

Hint

 

Source

2015-2016_SDNU_ACM-ICPC_Selection_Match_Round_1

错的代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod=1000000007;
struct point
{
    ll x,y;
}a[100050];
ll calc(point c,point d)
{
    return c.x*d.y-d.x*c.y;
}
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=1;i<=n;i++)
        {
            scanf("%lld %lld",&a[i].x,&a[i].y);
        }
        ll ans=0;
        a[n+1]=a[1];
        for(int i=2;i<=n+1;i++)
        {
            ans=(ans+calc(a[i-1],a[i])%mod)%mod;
        }
        cout<<ans<<'\n';
    }
}

ac的代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod=1000000007;
struct point
{
    ll x,y;
}a[100050];
ll calc(point c,point d)
{
    return (c.x*d.y-d.x*c.y);
}
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=1;i<=n;i++)
        {
            scanf("%lld %lld",&a[i].x,&a[i].y);
        }
        a[n+1]=a[1];
        ll ans=0;
        for(int i=2;i<=n+1;i++)
        {
            ans=(ans+calc(a[i-1],a[i])%mod+mod)%mod;
        }
        cout<<ans<<'\n';
    }
}

负数取余的公式为 （a%mod+mod）%mod  （orz好笨啊）

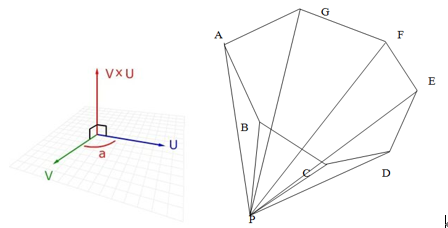
原引某博客的图

多边形的面积计算，多边形每个边两个端点跟原点组成一系列三角形，它们的面积有正负，所面积之和就是多边形的面积。 

这里选取的端点p为原点（逃）