1.题目要求
题目:最大连续子数组和(最大子段和)
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科》
2.实现代码
#include <iostream>
using namespace std;
int sum(int a[] ,int count)
{
int b[100];
int i;
int max;
b[0] = a[0];
max = b[0];
for (i = 1; i < count; i++)
{
if (b[i - 1] > 0)
b[i] = b[i - 1] + a[i];
else
b[i] = a[i];
if (b[i] > max)
max = b[i];
}
return max;
}
int main()
{
int count;
int a[100];
int i;
int max;
cin >>count;
for (i = 0; i < count; i++)
{
cin >> a[i];
}
max = sum(a, count);
cout << max;
return 0;
}
3.测试代码
程序流程图
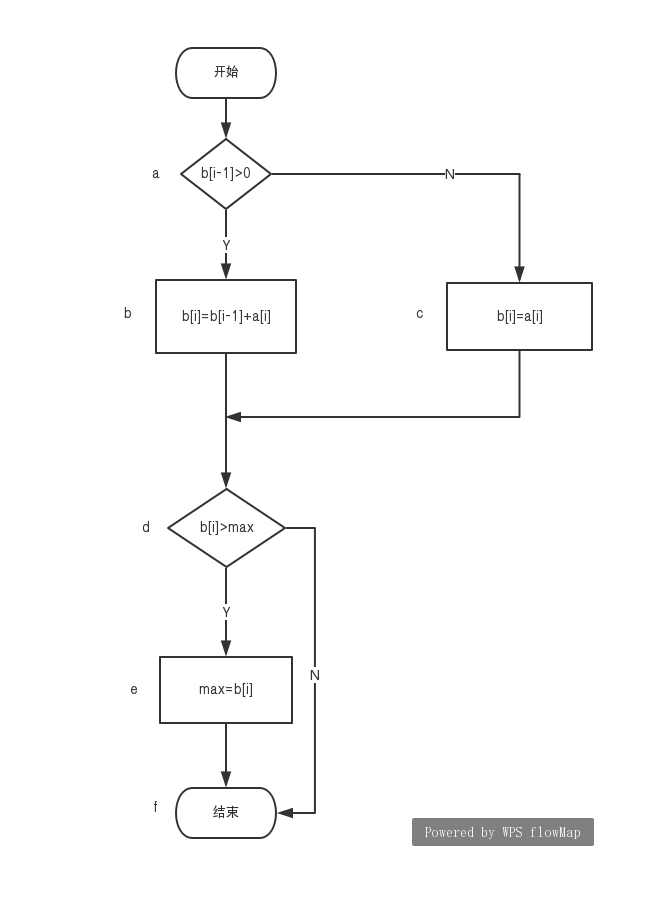
| 条件组合 | 执行路径 |
|---|---|
| b[i-1]>0,b[i]>max | abdef |
| b[i-1]<=0,b[i]>max | acdef |
| b[i-1]>0,b[i]<=max | abdf |
| b[i-1]<=0,b[i]<=max | acdf |
测试用例
a[]={1,5,9},max=15
a[]={-1,5,-1},max=5
a[]={-8,-2,-5,8},max=8
a[]={ -2,11,-4,13,-5,-2},max=20
TEST_METHOD(TestMethod1)
{
int max, num[3] = { 1,5,9 };
max = sum(num, 3);
Assert::AreEqual(max, 15);
}
TEST_METHOD(TestMethod2)
{
int max, num[3] = { -1,5,-1 };
max = sum(num, 3);
Assert::AreEqual(max, 5);
}
TEST_METHOD(TestMethod3)
{
int max, num[4] = { -8,-2,-5,8 };
max = sum(num, 4);
Assert::AreEqual(max, 8);
}
TEST_METHOD(TestMethod4)
{
int max, num[6] = { -2,11,-4,13,-5,-2 };
max = sum(num, 6);
Assert::AreEqual(max, 20);
}
4.测试结果
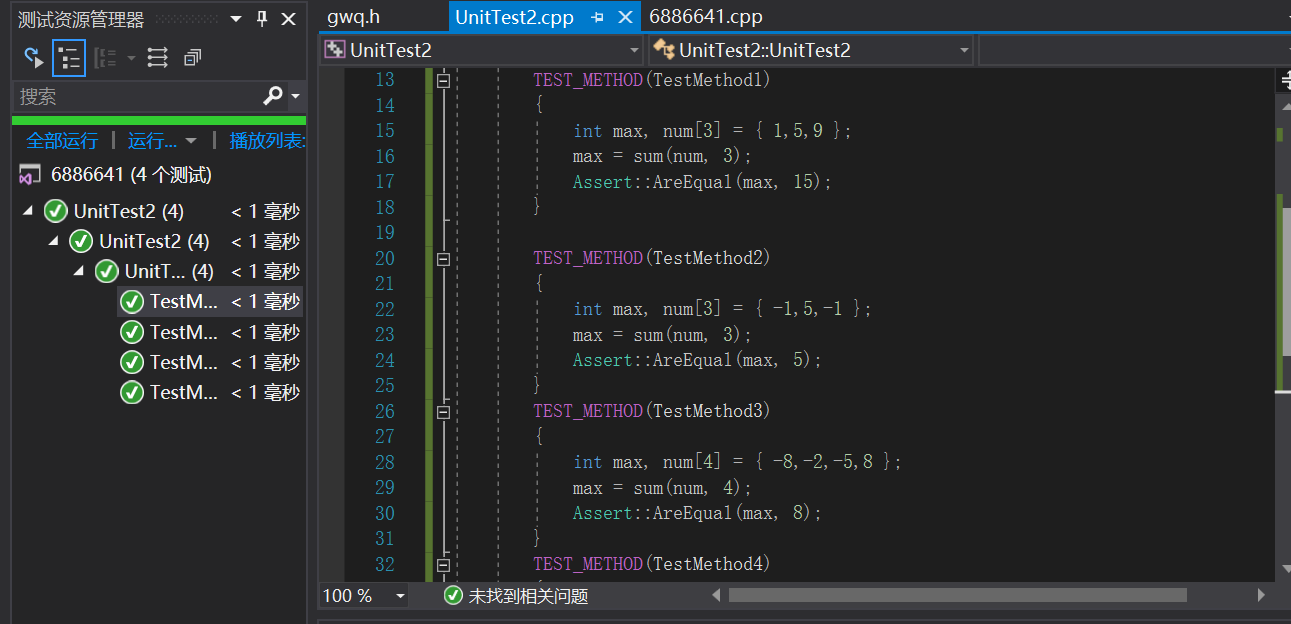


 posted on
posted on

