CF786B Legacy

CF786B Legacy

题意：

给定 \(n\) 个点，有三种操作：
1 x y w 表示 \((x,y)\) 连接一条权值为 \(w\) 的边
2 x l r w 表示从 \(x\rightarrow [l,r]\) 中的每个点连接一条权值为 \(w\) 的边
3 x l r w 表示从 \([l,r]\) 中的每一个点向 \(x\) 连接一条权值为 \(w\) 的边。

求从 \(s\) 开始到其他地方的最短路。没有则输出 \(-1\).

分析：

这题又是一道神仙题目。

当然，像图上这样建边自然是不行的，因为边数太多。

看到区间，考虑 线段树优化建图。

然后，从 \(x\) 到 \([l,r]\) 就可以表示成：从 \(x\) 向线段树中表示 \([l,r]\) 的区间和点连接一条边。比如 \(x=1,l=2,r=4\)，就可以表示成： \((1,2),(1,[3,4])\)。

从区间到点就是反过来就行了。

但是，线段树上每一个父亲节点，都要向左右儿子连接一条权值为 \(0\) 的双向边，然后最短路就是 \(0\) ... 显然用一个线段树自然不行，我们考虑建两个线段树：

一个从父亲连边到儿子，另一个从儿子连边到父亲。

然后，这两个线段树底部的节点，是通用的（就是没有表示区间的点）。

记住标号：底部是 \([1,n]\) ，第一个向下建边线段树从 \(n+1\) 开始标号，第二个线段树从上一个线段树标号的最大值开始标号，并且记录一个父节点左右儿子的编号。

注意，标号时当 \(l==r\) 时，表示到底部，和线段树一般父节点不一样标号，编号为其本身。

操作一就是正常的 \((x,y)\) 连边，重要的是操作二三。

二：

从点到区间，所以我们建立 从 \(x\) 点到第一个线段树的 \([l,r]\) 区间的边

为什么呢？因为第一棵线段树是从上向下建边。我们可以通过 \(x\) 代表的点，经过权值 \(w\) 到达 底部实际编号 \([l,r]\) 中的每一个点。

因此，搜索线段树时则有 \(add(x,区间编号,w)\) .

注意需要从第一棵树的根节点 \(root1\) 开始搜索。

三：

从区间到点，所以我们建立 从第二个线段树 \([l,r]\) 区间到 \(x\) 点的边

同理，第二棵线段树是从下往上建边，我们可以通过 底部实际编号 \([l,r]\) 的点，经过权值 \(w\) 到达 \(x\) 点。

给一组样例模拟一下：

\\输入
4 3 1
3 4 1 3 1
2 1 2 4 2
1 2 3 3
\\输出
0 2 2 1

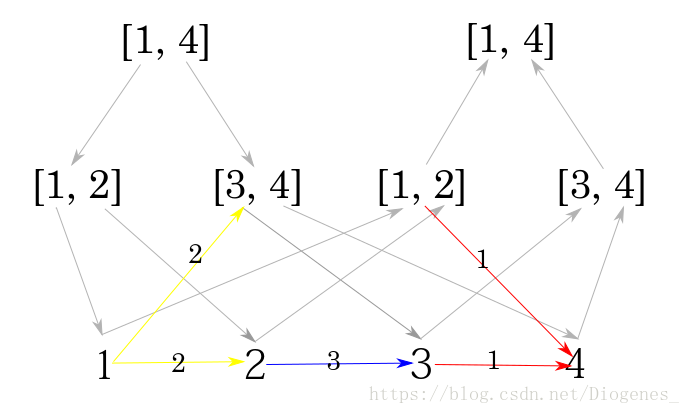
建完图之后长这样：图源

然后，从起点跑最短路就行了。不用四怕发，因为边数有可能很多。

代码：

#include<bits/stdc++.h>
#define ll long long
#define int long long 
#define pii pair<int,int> 
#define mk make_pair 
using namespace std;

const int N=2e6+5,D=5e5,M=5e5+5;
// const ll inf=1e17;

int head[N],ver[N],tot,nxt[N];
int n,Q,s,cnt,root1,root2;
int lc[M],rc[M],vis[M];
ll edge[N],dis[N];
void add(int x,int y,ll z){
    ver[++tot]=y; nxt[tot]=head[x]; head[x]=tot; edge[tot]=z;
}

void build1(int &x,int l,int r){
    if(l==r){ x=l; return;}
    x=++cnt;//数组模拟链表
    int mid=l+r>>1; 
    build1(lc[x],l,mid); build1(rc[x],mid+1,r);
    add(x,lc[x],0ll); add(x,rc[x],0ll);
}
void build2(int &x,int l,int r){
    if(l==r){x=l;return;}
    x=++cnt; int mid=l+r>>1;
    build2(lc[x],l,mid); build2(rc[x],mid+1,r);
    add(lc[x],x,0ll); add(rc[x],x,0ll);
}
int L,R;
void connect(int x,int l,int r,int u,int w,int op){
    if(L<=l&&r<=R){//完全覆盖，根据种类加边
        if(op==2) add(u,x,w);
        // cout<<u<<" "<<x<<" "<<w<<endl; 
        else add(x,u,w);
        // cout<<x<<" "<<u<<" "<<w<<endl; 
        return;
    }
    int mid=l+r>>1;
    if(L<=mid) connect(lc[x],l,mid,u,w,op);
    if(R>mid) connect(rc[x],mid+1,r,u,w,op);
}
priority_queue<pii> q;
void dijkstra(int s){
    memset(dis,0x3f,sizeof(dis));
    dis[s]=0;
    q.push(mk(0,s));
    while(!q.empty()){
        int x=q.top().second; q.pop();
        // cout<<x<<endl;
        if(vis[x]) continue;
        vis[x]=1;
        for(int i=head[x];i;i=nxt[i]){
            int y=ver[i],z=edge[i]; 
            // cout<<x<<" "<<y<<endl;
            if(dis[y]>dis[x]+z){
                dis[y]=dis[x]+z;
                q.push(mk(-dis[y],y));
            }
        }
    }
}

signed main(){
    cin>>n>>Q>>s; cnt=n;//建立边的要求，线段树的节点从 n+1 开始编号
    build1(root1,1,n); build2(root2,1,n);
    while(Q--){
        int op,x,y,l,r;ll w; scanf("%lld",&op);
        if(op==1){
            scanf("%lld%lld%lld",&x,&y,&w);
            add(x,y,w);//因为上面对叶子节点的处理，可以直接加边
        }
        else if(op==2){
            scanf("%lld%lld%lld%lld",&x,&L,&R,&w);
            connect(root1,1,n,x,w,2);
        }
        else{
            scanf("%lld%lld%lld%lld",&x,&L,&R,&w);
            connect(root2,1,n,x,w,3);
        }
    }
    dijkstra(s);
    for(int i=1;i<=n;i++) printf("%lld ",dis[i]>=1e17?-1:dis[i]); 
    system("pause");
    return 0;   
}