基环树

基环树：

定义：

基环树，又叫环套树，最显著的特点就是有 \(n\) 个点 \(n\) 条边，导致这个图上出现了一个唯一的环，就像这样：

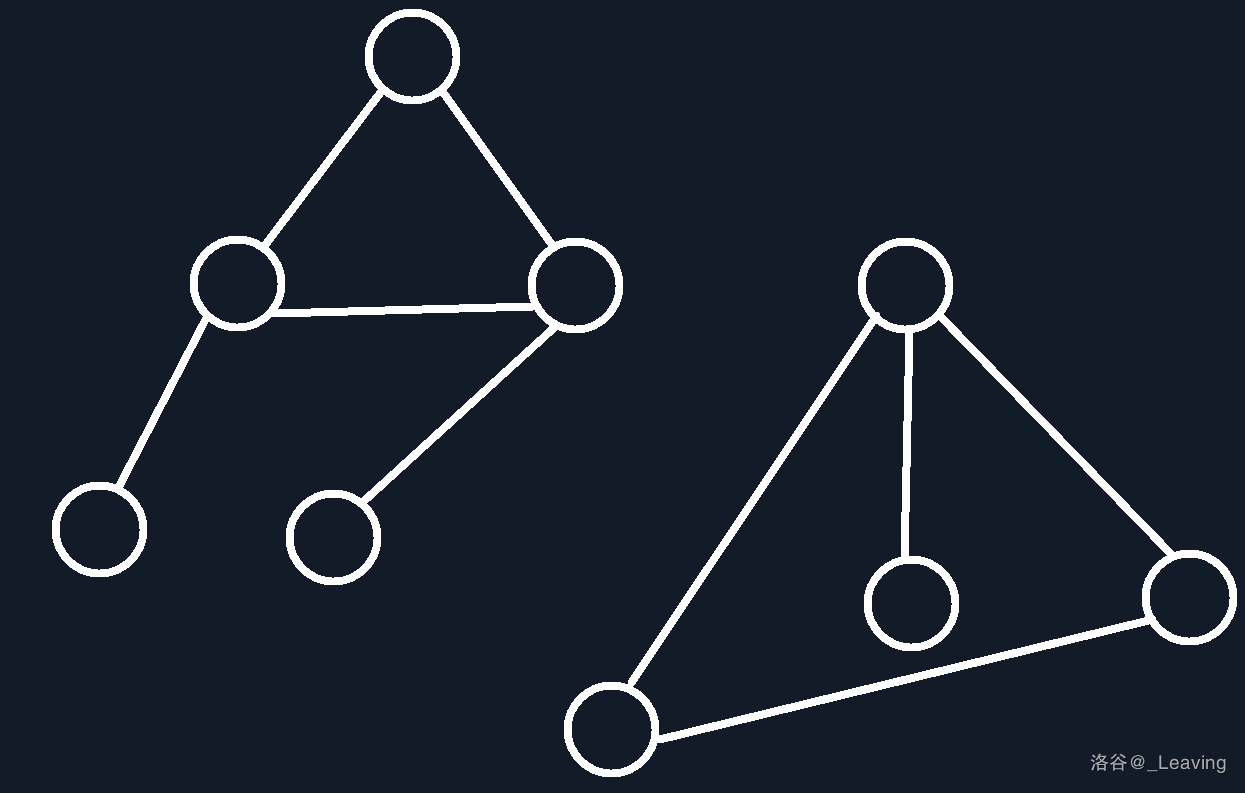
当然，如果保证这 \(n\) 个点 \(n\) 条边构成的是一个连通图时才是唯一环，如果图不连通但是每个联通块点数都等于边数时，这个图就是一个基环树森林。可以有好几个环。就像这样：

方法：

1. 有一个环，把这个环抽出来，这样整个图就变成了一个环上面有几个子树。然后对子树进行操作，将信息合并到环上的节点，最后就能把一个图上的问题降到环上处理。

2. 忽略掉导致整棵树出现环的一条边，然后对剩下的树进行操作。

例题：

CF711D Directed Roads

题意：

给定 \(n\) 个点和 \(n\) 个无向边，要求给这些无向边设定方向，使图中不出现环。

分析：

我们建图还是需要建立有向边的，然后在 这些图上 , （题目上并没有说这些点在同一个图上），寻找到环：

• 非在环上的路径：随便设定方向，假设一共 \(z\) 条，则有 \(2^z\) 种可能。

• 在环上的路径：如果方向设定的形成一个圈，也就是同时顺时针或逆时针，才能够形成环。假设有 \(n\) 个环，每个环上有 \(w[i]\) 个点，环上方向设定的方案数就是：

\[\prod\limits_{i=1}^n (2^{w[i]}-2) \]

发现 \(z=n-\sum\limits_{i=1}^n w[i]\)，因此答案为：

\[2^z \times \prod\limits_{i=1}^n (2^{w[i]}-2) \]

此时还有一个找环的技巧：根据深度 \(dep\) 和 \(vis\) 标记查找：

• 如果 \(y\) 没有 \(vis\) 标记，将 \(vis[y]=1\) 后继续搜索，将深度 \(+1\).
• 如果 \(y\) 有 \(vis[y]=1\) ，说明在搜索的过程中这个点被搜索过一次， 而且已访问过的结点不是上一步访问的结点，则说明存在环。环的长度即为 \(dep[y]-dep[x]+1\) ，也就是深度之差。
• 访问完某个节点后，将这个节点赋值为 \(vis[x]=2\) 。表示该节点所有邻接边访问完了，其他节点到这个节点不可能再形成环（因为所有出边已经访问完了）

总结来说，就是：

深度优先遍历图，如果在遍历的过程中，发现某个结点有一条边指向已访问过的结点，并且这个已访问过的结点不是上一步访问的结点，则表示存在环。

代码：

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=5e5+5,mod=1e9+7;

vector<int> v[N];
int dep[N],vis[N],mul[N],n;
int w[N],top;
int huan=0,res=1;
void dfs(int x,int d){
    dep[x]=d,vis[x]=1;
    for(auto y:v[x]){
        if(!vis[y]) dfs(y,d+1);
        else if(vis[y]==1) w[++top]=dep[x]-dep[y]+1;//找到每一个环的长度
    }
    vis[x]=2;//所有出边访问完成，跟这个点没关系了
}

signed main(){
    cin>>n; mul[0]=1; for(int i=1;i<=n;i++) mul[i]=(mul[i-1]*2)%mod;
    for(int i=1,x;i<=n;i++){
        scanf("%d",&x); v[i].push_back(x);
    }
    for(int i=1;i<=n;i++) if(!dep[i]) dfs(i,1);
    for(int i=1;i<=top;i++){
        huan+=w[i];
        res=(res*(mul[w[i]]-2+mod))%mod;
    }
    res=mul[n-huan]*res%mod;
    cout<<res<<endl;
    return 0;
}