主席树
主席树
引入:
一个问题:给定 \(n\) 个数,一共 \(m\) 次询问,每次都要询问 \([l,r]\) 的第 \(k\) 大的数,其中 \(n,m,l,r\) 均不超过 \(2 \times 10^5\)。
解决:
暴力想法:
显而易见,最暴力的方法就是区间 \(sort\) 之后输出第 \(k\) 个数。肯定不超时
主席树:
针对这类问题,出现了 可持久化线段树 。
意义是给线段树增加一些历史节点维护历史数据,使得能在较短时间内查之前查过的数据。
图示如下:

图中的橙色节点位历史节点,其右边多出来的节点是新节点(修改节点)
构建:
主席树的点修改:
不同于普通线段树的是主席树的左右子树编号并不能够用计算得到,所以我们需要记录下来,但是对应区间还是没问题。
//节点x表示区间[l,r],修改点为p,修改值根据题意设定
int modify(int x,int l,int r){
int now=++cnt;
lc[now]=lc[x]; rc[now]=rc[x]; sum[now]=sum[x]+1;//根据模板题建造新节点
if(l==r){//递归底层
// sum[now]=t; 如果题目要求是 sum 加 t 再这样弄,上面+1去掉
return now;
}
int mid=l+r>>1;
if(p<=mid) lc[now]=modify(lc[now],l,mid);
else rc[now]=modify(rc[now],mid+1,r);
return now;
}
区间修改:
没看
询问,查询区间历史和
int query(int x,int l,int r,int L,int R){//节点x代表区间[l,r]
if(!x) return 0;//子树不存在
if(L<=l&&r<=R) return sum[x];
if(L<=mid) ans+=query(lc[x],l,mid,L,R);
if(R>mid) ans+=query(rc[x],mid+1,r,L,R);
return ans;
}
复杂度分析:
修改,查询都是 \(O(\log n)\) 级别的
例题:
题意:
询问区间 \([l,r]\) 的最大值
分析:
先考虑 \([1,r]\) 的情况。
由提议知道,我们要对区间进行排序,是在初始化时就需要排序,而且要离散化。
排序离散化完毕后,以离散化数组建立主席树:
设 \(i\) 属于区间 \([1,n]\) ,对原数组的 \([1,i]\) 区间的数做统计:
有序的插入节点到离散化数组的主席树中,记录好原数组每个节点对应的线段树起点。
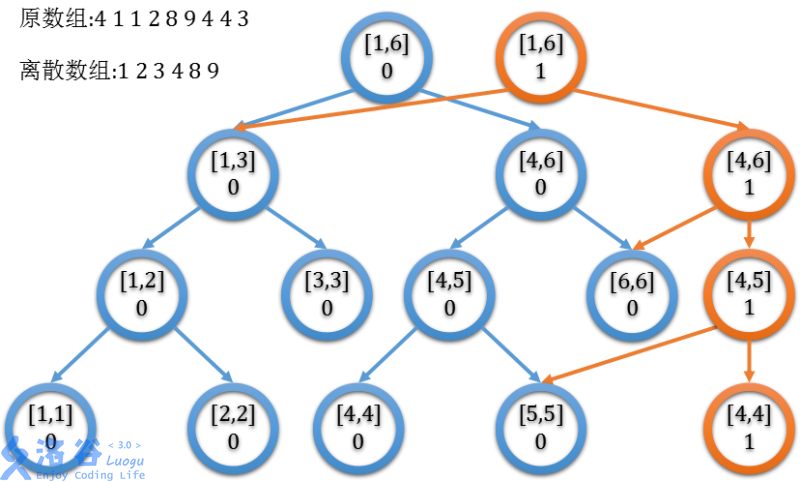
对于这题样例,有一些示意图,这里的橙色点是新节点。
- \([1,1]\) 的情况:
- \([1,4]\) 的情况:
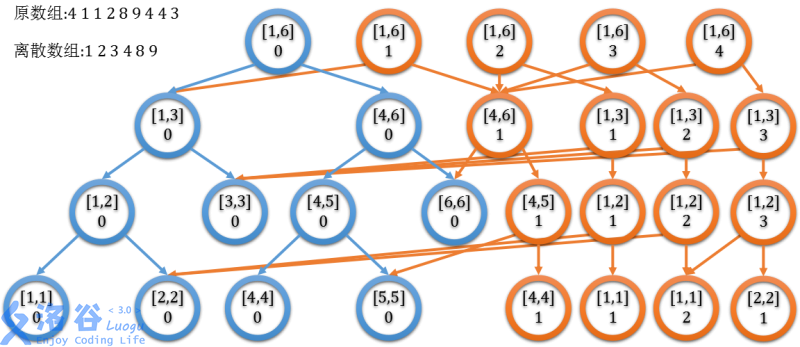
情况以此类推。
for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[i]=a[i];
sort(b+1,b+n+1);
int q=unique(b+1,b+n+1)-b-1;
build(rt[0],1,q);
for(int i=1;i<=n;i++){
p=lower_bound(b+1,b+q+1,a[i])-b;//找最小下标的匹配值
rt[i]=modify(rt[i-1],1,q,p)
}
按照上面的做法构建的主席树是方便我们查找第 \(k\) 小值。
因为我们是以离散数组构建的主席树,那么从根节点出发,左子树部分的数必定不大于右子树部分的数。
于是可以将左儿子的节点个数 \(x\) 和 \(k\) 比较:
- 若 \(k \leq x\) ,则第 \(k\) 小值一定在左子树里面。
- 若 \(k > x\) ,则第 \(k\) 小值一定在右子树里面。
然后继续递归往下走,记住当前往右子树,需要把 \(k\) 减去左子树的数的个数,然后再搜索值。
例如查找 \([1,4]\) 中第 \(2\) 小的值,图示如下:
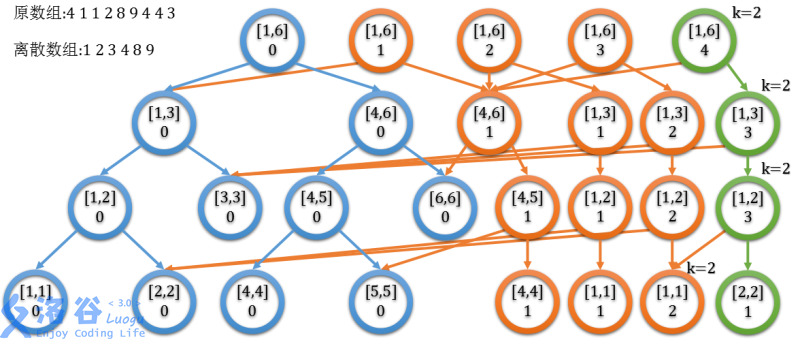
绿色节点为该值存在的区间位置。
注意:第二个绿色节点才是绿色根节点的左子树,因为左子树表示的区间 是靠前的那一半
总结:
- 数组离散化。
- 以离散化的数组为基础,建一个全为 \(0\) 的线段树,称作基础主席树。
- 对原数据中每一个 \([1,i]\) 区间统计,有序的插入新节点。
- 对于查询第 \(k\) 小值的操作,找到 \([1,r]\) 对应的根节点,按照线段树的方法操作即可。
解决问题:
其实,解决方案就是 \([1,r]\) 减去 \([1,l-1]\) ,因为统计的是数,所以直接减就行。
//初始的x,y表示l-1,r
int query(int x,int y,int l,int r,int k){
int ans,mid=l+r>>1,num=sum[lc[y]]-sum[lc[x]];//主席树区间是统计好的,只需要减一下
if(l==r) return l;//找到目标数字
if(num>=k) ans=query(lc[x],lc[y],l,mid,k);//左儿子里面查第k小的数
else ans=query(rc[x],rc[y],mid+1,r,k-num);//右子树需要改变k的值,然后查
return ans;
}
代码:
#include<bits/stdc++.h>
using namespace std;
const int M=2e5+5;
int cnt,n,m;
int sum[M<<5],rt[M],lc[M<<5],rc[M<<5];
int a[M],b[M],p;//p位修改点
void build(int &x,int l,int r){
x=++cnt;//新建节点的过程
if(l==r) return;
int mid=l+r>>1;
build(lc[x],l,mid); build(rc[x],mid+1,r);
}
//节点x表示区间[l,r],修改点为p,修改值根据题意设定
int modify(int x,int l,int r,int pos){
int now=++cnt;
lc[now]=lc[x]; rc[now]=rc[x]; sum[now]=sum[x]+1;//根据模板题建造新节点
if(l==r){//递归底层
// sum[now]=t; 如果题目要求是 sum 加 t 再这样弄,上面+1去掉
return now;
}
int mid=l+r>>1;
if(pos<=mid) lc[now]=modify(lc[now],l,mid,pos);
else rc[now]=modify(rc[now],mid+1,r,pos);
return now;
}
//初始的x,y表示l-1,r
int query(int x,int y,int l,int r,int k){
int ans,mid=l+r>>1,num=sum[lc[y]]-sum[lc[x]];//主席树区间是统计好的,只需要减一下
if(l==r) return l;//找到目标数字
if(num>=k) ans=query(lc[x],lc[y],l,mid,k);//左儿子里面查第k小的数
else ans=query(rc[x],rc[y],mid+1,r,k-num);//右子树需要改变k的值,然后查
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[i]=a[i];
sort(b+1,b+n+1);
int q=unique(b+1,b+n+1)-b-1;
build(rt[0],1,q);
for(int i=1;i<=n;i++){
p=lower_bound(b+1,b+q+1,a[i])-b;//找最小下标的匹配值
rt[i]=modify(rt[i-1],1,q,p);
}
while(m--){
int l,r,k; scanf("%d%d%d",&l,&r,&k);
int ans=query(rt[l-1],rt[r],1,q,k);
printf("%d\n",b[ans]);
}
system("pause");
return 0;
}



