笛卡尔树
笛卡尔树
大部分内容来自 OI-WIKI
定义:
笛卡尔树是一种二叉树,每一个结点由一个键值二元组 \((k,w)\) 构成。
要求 \(k\) 满足二叉搜索树的性质,而 \(w\) 满足堆的性质。
如果笛卡尔树的 \(k,w\) 键值确定,\(k,w\) 互不相同,那么这个笛卡尔树的结构是唯一的。
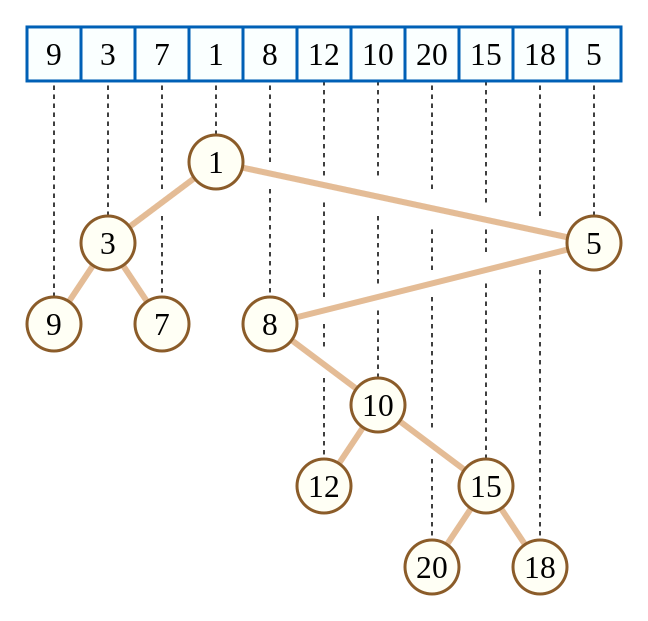
上面这棵笛卡尔树相当于把数组元素值当作键值 \(w\) ,把数组下标当作键值 \(k\) .
显然可以发现:这棵树的键值 \(k\) 满足二叉搜索树的性质,而键值 \(w\) 满足小根堆的性质。
其实这是一种特殊的笛卡尔树,键值 \(k\) 正好对应数组下标。更一般的情况则是任意二元组构建的笛卡尔树。
构建:
栈构建:
将元素按键值 \(k\) 排序(也就是下标),先后插入当前的笛卡尔树中,那么我们每次插入的元素必然在这个树的右链(从根节点一直往右子树走形成的链) 的末端。
执行这样一个过程:
- 从下往上比较右链节点与当前加入节点 \(x\) 的键值 \(w\):
-
如果找到右链上的节点 \(u\) 满足 \(w_u<w_x\) ,那么把 \(x\) 接到 \(u\) 的右儿子上,而以 \(u\) 为根的右子树变成了 \(x\) 的左子树,然后停止加入过程。
-
如果没有找到右链上的节点,那么 \(x\) 就是新根,把原来的树当成 \(x\) 的左儿子。
每次添加值都需要进行一次这样的比较。
过程图:
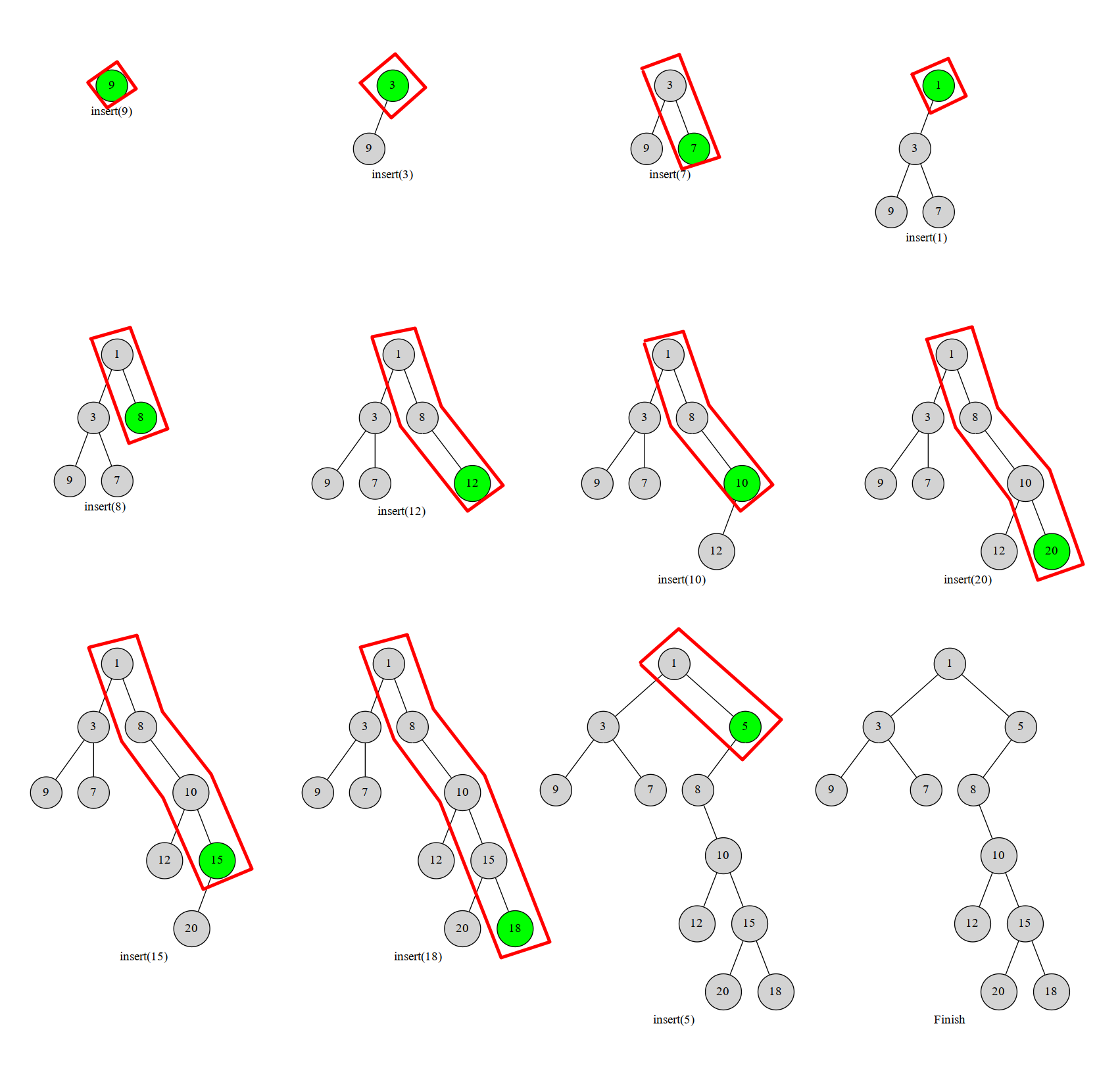
显然,每个数最多进出右链一次,这个过程可以用栈进行维护,栈中维护当前笛卡尔树右链上的节点,不在右链就弹出,时间复杂度为 \(O(n)\)
代码:
for(int i=1;i<=n;i++){
while(top&&a[stk[top]]>a[i]) son[i][0]=stk[top--];//当前节点成为了i的左儿子
if(stk[top]) son[stk[top]][1]=i;//还存在,说明没有遍历到头,因此该点对应的右儿子设置成i
stk[++top]=i;//新儿子进节点
}
例题:
题意:
给定一个 \([1-n]\) 的排列 \(p\), 构建一颗二叉树满足:
- 每个节点编号满足二叉搜索树性质
- 节点 \(i\) 的权值为 \(p_i\) ,每个节点权值满足小根堆性质。
分别求每个节点左 \(/\) 右儿子乘节点编号的异或值之和
分析:
就是构建一颗笛卡尔树,然后计算就行了:
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int n;
int a[N],son[N][2];
int sta[N],top;
int rans,lans;
int read(){//1e7的读入....记得快读
int res=0; char ch=getchar();
while(ch>'9'||ch<'0') ch=getchar();
while(ch<='9'&&ch>='0'){
res=(res<<1)+(res<<3)+ch-'0'; ch=getchar();
}
return res;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
a[i]=read();
while(a[sta[top]]>a[i]&&top) son[i][0]=sta[top--];
if(sta[top]) son[sta[top]][1]=i;
sta[++top]=i;
}
for(int i=1;i<=n;i++){
lans=lans^(i*(son[i][0]+1));
rans=rans^(i*(son[i][1]+1));
}
cout<<lans<<" "<<rans<<endl;
system("pause");
return 0;
}
这里要注意的是:
-
栈中存储的每个节点的标号,并不是该节点对应的值
-
一定要弄清楚左右儿子的赋值情况。
性质(小根笛卡尔树):
-
以点 \(u\) 为根的子树是一段连续极长区间,\(w_x\) 是区间的最小值,区间在保证最小值不变的情况下不能再向两边延长。
-
区间 \([a,b]\) 的最小值为 \(w_{lca_{a,b}}\)
-
对于有序数列 \(x\) 及随机排列 \(y\) ,笛卡尔树的期望高度为:
\(E(dep_i)=H(i)+H(n-i+1)\) ,其中调和级数 \(H(n)=\sum_{i=1}^x \frac{1}{i}\)
关于这个可以看看 [AGC028B] Removing Blocks 这道题,我在博客里也写了题解。
总结:
笛卡尔树主要用于解决最大/最小值问题,以及通过记录时间关于插入删除的问题。



