最大流

最大流：

定义：

有一张图，要求从源点流向汇点的最大流量（可以有很多条路到达汇点）

概念：

残量网络：

定义 \(c_f(u,v)\) 为边的流量之差，表示这条边的容量和流量之差，即：

\[c_f(u,v)=c(u,v)-f(u,v) \]

对于流函数 \(f\) ，残存网络 \(G_f\) 是网络 \(G\) 中 所有节点和剩余容量大于 \(0\) 的边 构成的子图。

形式化的定义： \(G_f=(V_f=V,E_f=\left\{(u,v)\in E,c_f(u,v)>0\right\})\)

注意：剩余容量大于零的边可能不在原图 \(G\) 中。

残量网络中包括了那些还剩了流量空间的边构成的图，也包括反向边。

增广路：

在原图 \(G\) 中若一条从源点到汇点的路径上所有边的 剩余容量大于零，这条路就被称为增广路。

或者说，在残存网络 \(G_f\) 中，一条从源点到汇点的路径被称为增广路.

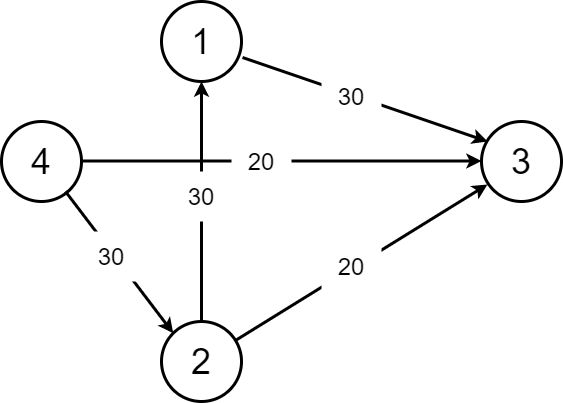
在这张图中，从 \(4 \rightarrow 3\), 先走 \(f_(4,3)=20\) 这条边。

然后判断 \(4 \rightarrow 2 \rightarrow 3\) 这条增广路 的总流量为 \(20\), \(4 \rightarrow 2 \rightarrow 1 \rightarrow 3\) 这条路总流量为 \(30\).

因此最大流就是 \(20+30=50\)

算法：

\(EK\) 算法：

思想：用 \(BFS\) 不断寻找增广路，直到网络上不存在增广路为止。

分析：

每轮寻找增广路的过程中，只考虑图中所有 \(f(u,v)<c(u,v)\) 的边，用 \(BFS\) 找到任意一条 \(s \rightarrow t\) 的路径，同时计算出路径上个边的剩余容量的最小值 \(minn\) ,则网络的流量可以增加 \(minn\)。

同时，当一条边流量 \(f(u,v)>0\) 时，我们需要建立反向边 \(f(v,u)=-f(u,v)\) ,此时必定有 \(f(y,x)<c(y,x)\) 。

在该算法中，我们需要遍历正反边，利用 邻接表成对存储 的技巧，也就是
\(2^1=3,3^1=2\) 这样能相互得到，存储标号从 \(2\) 开始。

对于每条边，我们只记录剩余容量 \(c(u,v)-f(u,v)\) 。

当一条边经过一条流量为 \(e\) 的边，令 \((u,v)\) 的剩余流量减少 \(e\) ,\((v,u)\) 的剩余容量增加 \(e\)。

想法就像这张图：

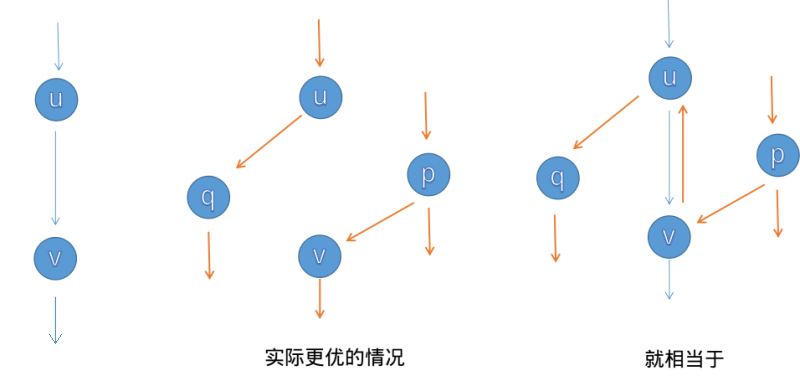
时间复杂度为 \(O(nm^2)\) ，时间复杂度较高

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1005,M=2e5+5,inf=0x3f3f3f3f;
#define ll long long 

int head[N],nxt[M],ver[M],tot=1,edge[M];
int n,m,s,t;
ll maxflow;
int vis[N],incf[N],pre[N];
void add(int x,int y,int z){
    ver[++tot]=y; nxt[tot]=head[x]; head[x]=tot; edge[tot]=z;
    ver[++tot]=x; nxt[tot]=head[y]; head[y]=tot; edge[tot]=0;
}
void update(){
    int x=t;
    while(x!=s){
        int i=pre[x];
        edge[i]-=incf[t]; edge[i^1]+=incf[t];
        x=ver[i^1]; //继续回溯
    }
    maxflow+=incf[t];
}
bool bfs(){
    memset(vis,0,sizeof(vis)); queue<int> q; q.push(s); vis[s]=1; 
    incf[s]=inf;//各边剩余最小容量
    while(!q.empty()){
        int x=q.front(); q.pop();
        for(int i=head[x]; i; i=nxt[i]){
            int y=ver[i],z=edge[i]; 
            if(vis[y]||!z) continue;
            incf[y]=min(incf[x],z);//限制流量和当前点能流的最大流量比较
            pre[y]=i;//记录前驱，用来找到最长路的实际方案
            q.push(y); vis[y]=1;
            if(y==t) return 1; 
        }
    }
    return 0;
}
int main(){
    cin>>n>>m>>s>>t;
    for(int i=1,x,y,z;i<=m;i++){
        scanf("%d%d%d",&x,&y,&z); add(x,y,z);
    }
    while(bfs()) update();//证明有一条新边可以更新
    cout<<maxflow<<endl;
    system("pause");
    return 0;
}

\(Dinic\) 算法：

\(EK\) 每轮会遍历整个残量网络，但只能找出一条增广路，属实是拉了属于是

我们可以利用 分层图 的性质(即满足 \(dep[u]+1=dep[v]\) 的边 \((u,v)\) 构成的子图) 。

流程：

1. 在残量网络上 \(BFS\) 求出节点的层次，构造分层图。

2. 在分层图上 \(DFS\) 寻找增广路，在回溯时实时更新剩余容量，另外，各个点可以流向多条出边，同时还需要剪枝等操作。

时间复杂度为 \(O(n^2m)\) ，实际上会更优。

当前弧优化：

每次增广一条路后可以看做 榨干 了这条路，既然榨干了就没有再增广的可能了。

但如果每次都扫描这些枯萎的边是很浪费时间的。

那我们就记录一下榨取到那条边了，然后下一次直接从这条边开始增广，就可以节省大量的时间。这就是 当前弧优化。

具体怎么实现呢，先把链式前向星的 \(head\) 数组复制一份，存进 \(cur\) 数组，然后在 \(cur\) 数组中每次记录“榨取”到哪条边了。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
const int inf=0x3f3f3f3f,N=5005,M=200005;
int nxt[M],ver[M],tot=1,edge[M],head[N];
int n,m,s,t;
ll maxflow;
int dep[N],incf[N],pre[N],cur[N];

void add(int x,int y,int z){
    ver[++tot]=y; edge[tot]=z; nxt[tot]=head[x]; head[x]=tot;
    ver[++tot]=x; edge[tot]=0; nxt[tot]=head[y]; head[y]=tot;
}

bool bfs(){
    memset(dep,0,sizeof(dep)); queue<int> q; q.push(s); dep[s]=1;
    while(!q.empty()){
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=nxt[i]){
            int y=ver[i],z=edge[i];
            if(dep[y]||!z) continue;
            q.push(y);
            dep[y]=dep[x]+1;
            if(y==t) return 1;
        }
    }
    return 0;
}

int dinic(int x,int flow){//flow表示限制流量
    if(x==t) return flow;
    int totflow=0;//从这个点总共可以增广多少流量
    for(int i=cur[x];i;i=nxt[i]){
        cur[x]=i;//记录上一次增广到哪条边了
        int y=ver[i],z=edge[i];
        if(dep[y]!=dep[x]+1||!edge[i]) continue;
        int canflow=dinic(y,min(flow,z));//表示这条增广路上能增加多少流量
        edge[i]-=canflow; edge[i^1]+=canflow;
        totflow+=canflow;//总共增加多少流量
        flow-=canflow;
        if(flow<=0) break;//当前点已经没有流量
    }
    return totflow;
}

int main(){
    cin>>n>>m>>s>>t;
    for(int i=1,x,y,z;i<=m;i++){
        scanf("%d%d%d",&x,&y,&z); add(x,y,z); 
    }
    while(bfs()){
        memcpy(cur,head,sizeof(head));
        maxflow+=dinic(s,inf);
    } 
    cout<<maxflow<<endl;
    system("pause");
    return 0;
}