并查集+带权并查集
并查集
概念:
并查集就是将数组中的数经过树状排列后,
如果寻找两个数是否属于同一集合,
直接找是否属于同一根节点的子树就可以。
路径压缩和按秩合并
路径压缩:
在每次执行 \(get\) 操作的同时,
把访问过的每个节点(也就是所查的元素的祖先,都直接指向树根)
每次 \(get\) 的均摊复杂度为 \(O(logn)\)
按秩合并:
意思就是,在合并时使得树的深度较小,也就是合并到当前深度较小的树上。
这样可以降低查询的时间复杂度,不过一般只写路径压缩即可。
初始代码:
-
并查集的存储
使用一个数组 \(fa\) 保存 \(i\) 父节点: \(fa[i]\) -
并查集的初始化:
设有 \(n\) 个元素,一开始每个元素各自构成一个集合,因此为:for(int i=1;i<=n;i++) fa[i]=i; -
并查集的 \(get\) 操作:
若 \(x\) 是树根,则 \(x\) 就是集合代表,否则递归访问 \(fa[x]\) 直到根节点:int get(int x){ if(x==fa[x]) return x;//找到根节点 return fa[x]=get(fa[x]);//递归+路径压缩,直接将fa[x]指向根节点 } -
并查集的 \(merge\) 操作(无按秩合并):
合并元素 \(x\) 和元素 \(y\) 的集合,等价于让 \(x\) 的树根作为 \(y\) 的树根的子节点:void merge(int x,int y){ fa[get(x)]=get(y); }
例题:
分析:
由于这道题需要计算路径,因此可以用数组 \(d[x]\) 来维护前面飞船的长度。
$d[x] $即为 \(x\) 数组距离根节点的长度是多少,可以用 \(sizes\) 数组来赋值 \(d[x]\) 。
同时,也需要 \(sizes\) 数组来计算一列中总体飞船数量。
最后,如果询问,我们直接算出两飞船 \(d\) 的差即可。
#include<bits/stdc++.h>
using namespace std;
const int N=31010;
int fa[N],n,t,i,j,d[N],sizes[N];//size为记录一列上有几个飞船
int get(int x){
if(x==fa[x])//查询到了根节点,则返回根节点
return x;
int root=get(fa[x]);//递归计算集合代表 root为树根
d[x]+=d[fa[x]];//维护d数组,对边权求和
return fa[x]=root;//直接指向树根
}
void merge(int x,int y){
x=get(x),y=get(y);
fa[x]=y,d[x]=sizes[y];//排在x前面是a,d[x]的大小是前面有多少个飞船
sizes[y]+=sizes[x];//合并,算总体飞船数量
}
int main()
{
scanf("%d\n",&t);
for(i=1;i<=30000;i++) fa[i]=i,sizes[i]=1;//fa表示排在x号战舰前面的那个战舰的编号
while(t--){
char ch=getchar();
scanf("%d %d\n",&i,&j);
if (ch=='M') merge(i,j);
else{
if (get(i)==get(j)) cout<<abs(d[i]-d[j])-1;
else cout<<"-1";
puts("");
}
}
return 0;
}
带权并查集
一般的并查集无法存储信息,因此需要带权并查集。
与普通并查集区别:
路径压缩
需要在 \(get(fa[x])\) 前面加一步赋值操作
将查找过程中每个父节点都设为最终得到的那个点
基于路径压缩,带权并查集就是
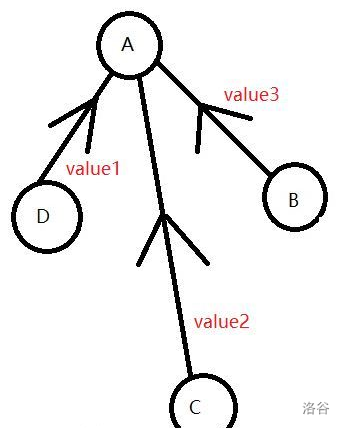
长成这个样子
因此,在路径压缩过程中,权值也应当做相应的更新
-
在路径压缩之前,每个节点都是与其父节点连接着,那个值也是与其父节点之间的权值
-
在两个并查集做合并的时候,权值也要做相应的更新
代码:
int find(int x){
if (x!=fa[x]){
int y=fa[x];
fa[x]=find(fa[x]);
val[x]+=val[y];
}
return fa[x];
}
其中,\(val\) 就是子节点的边权值加上父节点的边权值的和。
先记录下原本父节点的编号,压缩后父节点变成根节点,此时父节点的值已经是父节点到根节点的权值了,因此就可以得到当前节点到根节点的权值。
合并
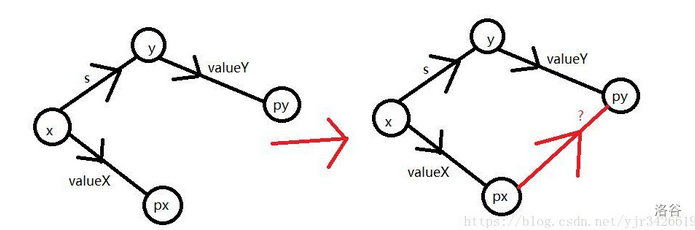
我们要将带有 \(x\) 的树挪到 \(y\) 上,因此先要找到他们的根节点 \(px\),\(py\)。
现在是要求 \(px\) 和 \(py\) 之间的权值是多少。
我们可以从这张图中看出来,已知 \(x\)到 \(px\),\(x\) 到 \(y\) 为读入的 \(s\),\(y\) 到 \(py\)
\(x\) 到 \(py\) 的两条路径长度相同
因此路径长度为 \((-val[x]+s+val[y])=px->py\)
代码:
int px = find(x),py = find(y);
if (px != py){
fa[px]=py;
val[px]=+val[y]+s-val[x];
}
3.例题理解
此道题差不多就是模板题,只要在判断二者在同一根节点时,其已经存在的权值是否与输入的权值相等就行
因此代码如下:
#include<bits/stdc++.h>
using namespace std;
int dis[105],fa[105],n,m,w;
int find(int x){
if(x!=fa[x]){
int root=fa[x];
fa[x]=find(fa[x]);
dis[x]+=dis[root];
}
return fa[x];
}
void merge(int x,int y,int w)//添加权值操作
{
int px=find(x),py=find(y);
if(px!=py){
fa[px]=py;
dis[px]=-dis[x]+dis[y]+w;
}
}
int main()
{
cin>>w;
while(w--){
cin>>n>>m;
for(int i=0;i<=n;i++) fa[i]=i,dis[i]=0;
bool flag=true;
while(m--){
int x,y,w;
cin>>x>>y>>w;
if(flag==false) continue;
x--;
if(find(x)!=find(y))//不是同一根节点
merge(x,y,w);
else
if((dis[x]-dis[y])!=w)
flag=false;
}
if(flag) cout<<"true"<<endl;
else cout<<"false"<<endl;
}
return 0;
}



