斜率优化DP
斜率优化 \(DP\)
引入:
通过一道题来引入吧:
题意:
给你一些物品,每个物品有大小,你可以选择多个背包装这些东西,背包费用由背包中物品大小决定,问你这些物品放进背包中,需要背包制作的总费用最少值。
分析:
这题暴力的 \(dp\) 方程得出来比较简单,记为:
这样就完成了暴力,时间为 \(O(n^2)\) ,这显然是不够过这道题的。
我们发现,一些值不用通过 \(dp\) 就能计算出来:
我们设 \(a[i]=sum[i]+i\), \(b[i]=sum[i]+i+L+1\) ,则原方程变为:
展开,移相,变为:
设 \(x=b[j]\), \(y=dp[j]+b[j]^2\) ,这个式子可以看成:
可以看作一条斜率为 \(2a[i]\) 的直线,对于每个 \(i\) 来说, \(a[i]\) 是确定的。
接下来的步骤跟线性规划类似:
我们将 \(dp[i]\) 的含义转化:
上述直线过点 \(P(b[j],dp[j]+b[j]^2)\) 时,直线在 \(y\) 轴的截距加上 \(a[i]^2\)
题目就询问的是这个截距的最小值。也就是经过这些点 \(P\) ,斜率为 \(2a[i]\) 的直线经过 \(y\) 轴时 \(y\) 坐标最小值是多少
初始时,直线斜率为 \(2a[i]\) ,画出图像如下:
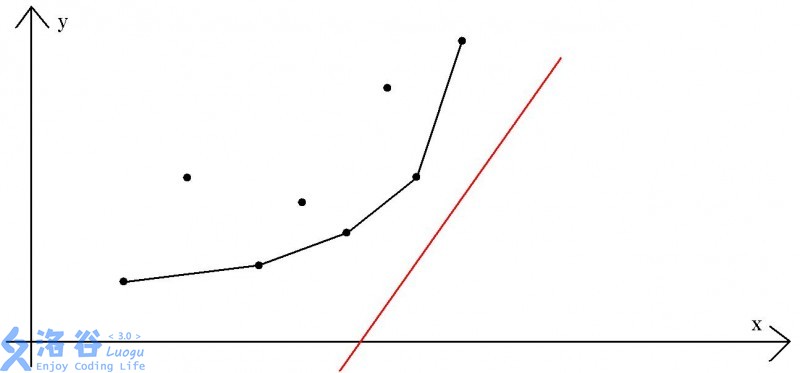
类似线性规划,我们将这条直线从下往上平移,碰到第一个点停下,截距即为最小。
本文中的 \(P\) 点组合成了一个下凸包,凸包中两点斜率单增,目标直线斜率 \(2a[i]\) 也是单增。
这里设 \(slope(x,y)\) 为 \(x,y\) 两点连接而成的直线的斜率
因此能得到结论: 满足条件的 \(P_j\) 为第一个 \(slope(P_j,P_{j+1})>2a[i]\) 的点。
我们使用 单调队列 维护这个凸包,因此有伪代码:
while(l<r&&slope(q[l],q[l+1])<2*a(i)) ++l;
//不满足条件
dp[i]=dp[q[l]]+(a(i)-b(q[l]))*(a(i)-b(q[l]));
//队首就是最优解
while(l<r&&slope(i,q[r-1])<slope(q[r-1],q[r])) --r;
//更加优秀的点
q[++r]=i;
删去队尾元素有以下图解释:
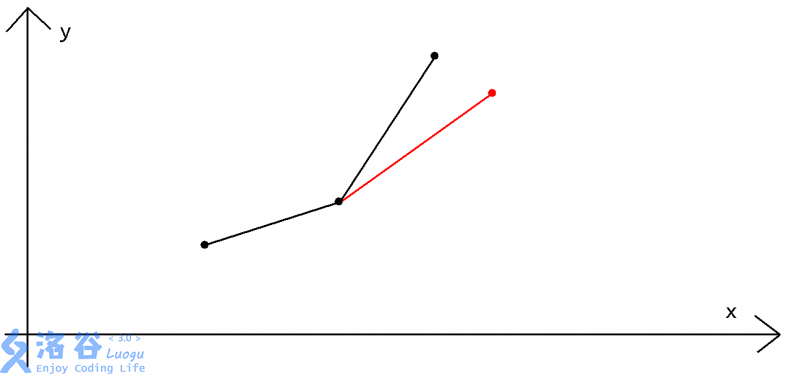
图中红色点为 \(i\) ,最上端黑色点为 \(q[r]\) 代表的点。
\(q[r]\) 在凸包内部,显然不是最优。
根据题意,列出计算公式就可以解决了
代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=50005;
int n,L;
double sum[N],dp[N];
int q[N],l,r;
double a(int i){ return sum[i]+i;}
double b(int i){ return a(i)+L+1;}
double X(int i){ return b(i);}
double Y(int i){return dp[i]+b(i)*b(i);}
double calc(int i,int j){
return ((Y(i)-Y(j))/(X(i)-X(j)));
}
//贺!
int main(){
cin>>n>>L;
for(int i=1;i<=n;i++) scanf("%lf",&sum[i]),sum[i]+=sum[i-1];
l=1,r=1;
for(int i=1;i<=n;i++){
while(l<r&&calc(q[l],q[l+1])<2*a(i)) ++l;
dp[i]=dp[q[l]]+(a(i)-b(q[l]))*(a(i)-b(q[l]));
while(l<r&&calc(i,q[r-1])<calc(q[r-1],q[r])) --r;
q[++r]=i;
}
cout<<(ll)dp[n]<<endl;
system("pause");
return 0;
}
例题:
[SDOI2016]征途
题意:
有 \(n\) 个值,让你分成 \(m\) 段,使方差最小。
分析:
我们将计算公式列出来:设 \(V_{sum}\) 为总路径长度, \(V_1,V_2...V_m\) 为每一段的路径长度,则有:
普通 \(DP\) 时间复杂度为 \(O(n^2m)\) 的,显然过不去,这时候就要用到斜率优化。
普通过程:
for(int i=1;i<=n;i++)for(int l=2;l<=m;l++)for(int j=1;j<i;j++)
dp[i][l]=min(dp[i][l],dp[j][l-1]+(sum[i]-sum[j])*(sum[i]-sum[j]));
我们依旧是定义 \(dp[i][j]\) 表示到第 \(i\) 段,分了 \(j\) 次的最小值。
上述转移式子可以转化成:
\(dp[i][l]+2*sum[i]*sum[j]=dp[j][l-1]+sum[i]^2+sum[j]^2\)
即 :斜率为 \(2sum[i]\) 的直线,要求过点 \(P(sum[j],sum[i]^2+sum[j]^2)\) 时在 \(y\) 轴上的截距最小。
然后使用套路就行了,第一个斜率 \(slope(P_j,P_j+1)>2sum[i]\) 就是答案。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=3005,INF=0x3f3f3f3f;
int n,m;
int val[N],sum[N],g[N];
int dp[N];
int q[N];
double X(int x){return sum[x];}
double Y(int x){return g[x]+sum[x]*sum[x];}
double slope(int x,int y){
return (Y(x)-Y(y))/(X(x)-X(y));
}
int calc(int x,int y){return g[x]+(sum[y]-sum[x])*(sum[y]-sum[x]);}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
scanf("%lld",&val[i]);
sum[i]=sum[i-1]+val[i];
g[i]=sum[i]*sum[i];
}
for(int l=1;l<m;l++){
int L=1,R=1; q[1]=l;
for(int i=l+1;i<=n;i++){
while(L<R&&slope(q[L],q[L+1])<2*sum[i]) ++L;
dp[i]=g[q[L]]+(sum[i]-sum[q[L]])*(sum[i]-sum[q[L]]);
while(L<R&&slope(i,q[R-1])<slope(q[R],q[R-1])) --R;
q[++R]=i;
}
for(int i=1;i<=n;i++) g[i]=dp[i];
}
cout<<m*dp[n]-(sum[n]*sum[n])<<endl;
system("pause");
return 0;
}



