线段树-扫描线

图片来源

扫描线：

使用一条垂直于 \(x\) 轴的直线，从左到右扫描这个图形，例如这样：

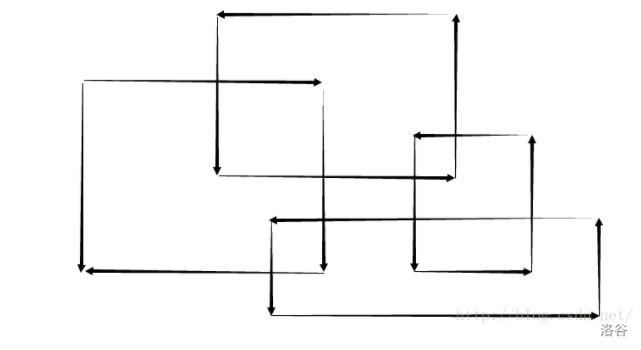
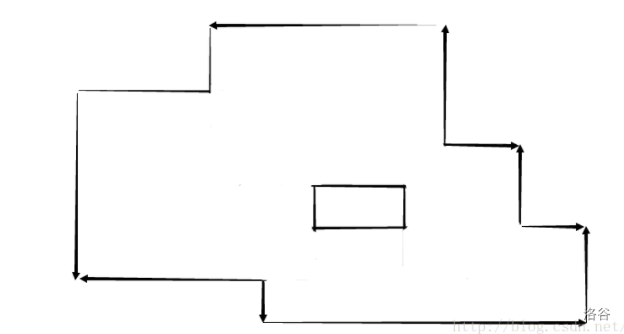
只有碰到矩形的左边界或者是右边界时这个线段所扫描到的情况才会改变。

因此，我们可以把所有矩形的入边和出边按 \(x\) 值排序,根据 \(x\) 值从小到大去处理。

用线段树维护扫描到的情况。

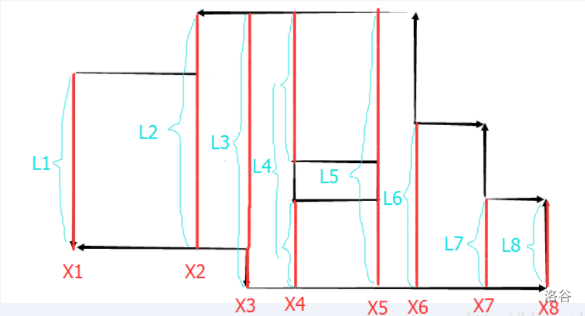
如上图：
如果碰到矩形的入边，就把这条边加入。如果碰到出边，就拿走，红色部分就是有线段覆盖度部分。求面积，只需要知道图中的 \([l1-l8]\).

计算过程模拟：

\(X_1\):

首先遇到 \(X_1\),将第一条线段加入线段树，由线段树统计得到线段长度为 \(L_1\).

\(X_2\):

然后继续扫描到 \(X_2\) ,此时要进行两个动作：

1. 计算面积，目前扫过的面积 \(S=L_1*(X_2-X_1)\)
2. 更新线段。由于 \(X_2\) 处仍然是入边，所以往线段树中又加了一条线段，加的这条线段可以参考三幅图中的第一幅。

然后线段树自动得出此时覆盖的线段长度为 \(L_2\) (注意两条线段有重叠部分，重叠部分的长度只能算一次).

\(X_3\):

继续扫描到 \(X_3\)，步骤同 \(X_2\)

1. 先计算 扫过的面积 \(S+=L_2*(X_3-X_2)\)
2. 再加入线段，得到 \(L_3\).

\(X_4\):

扫描到 \(X_4\) 有些不一样了。

首先还是计算 \(S+=L_3*(X_4-X_3)\)

然后这时遇到了第一个矩形的出边，这时要从线段树中删除一条线段。

删除之后的结果是线段树中出现了 \(2\) 条线段，线段树自动维护这两条线段的长度之和 \(L_4\)

代码介绍：

首先将一个矩形的入边和出边都存起来，根据 \(x\) 值排序：

struct LINE{
	int x;//横坐标 
	int y1,y2;//矩形纵向线段的左右端点 
	bool In;//标记是入边还是出边 
	bool operator < (const Line &B)const{ return x < B.x;}
}Line[maxn]; 

扫描的时候，需要两个变量

1. \(prel\) ，存前一个 \(x\) 操作结束后的 \(l\) 值

2. \(X\)，前一个横坐标

假设一共有 \(ln\) 条线段：

int PreL=0;//前一个L值,刚开始是0，所以第一次计算时不会引入误差 
int X;//X值 
int ANS=0;//存累计面积
int I=0;//线段的下标 
 
while(I < Ln){
	//先计算面积 
	ANS+=PreL*(Line[I].x-X);
	X=Line[I].x;//更新X值
	//对所有X相同的线段进行操作 
	while(I < Ln && Line[I].x == X){
		//根据入边还是出边来选择加入线段还是移除线段 
		if(Line[I].In)//加入线段 
        	   Cover(Line[I].y1,Line[I].y2-1,1,n,1);
		else//移出线段         
    		   Uncover(Line[I].y1,Line[I].y2-1,1,n,1);
		++I;
	} 
}

如果直接根据 \(x\) 值存的话，有可能爆掉，因此我们需要离散化：

int Rank[maxn],Rn;
void SetRank(){//调用前，所有y值被无序存入Rank数组，下标为[1..Rn] 
	int I=1;
	//第一步排序 
	sort(Rank+1,Rank+1+Rn); 
	//第二步去除重复值 
	for(int i=2;i<=Rn;++i) if(Rank[i]!=Rank[i-1]) Rank[++I]=Rank[i];
	Rn=I;
	//此时，所有y值被从小到大无重复地存入Rank数组，下标为[1..Rn] 
} 
int GetRank(int x){//给定x，求x的下标 
	//二分法求下标 
	int L=1,R=Rn,M;//[L,R] first >=x
	while(L!=R){
		M=(L+R)>>1;
		if(Rank[M]<x) L=M+1;
		else R=M;
	}
	return L;
}

此时，线段树的下标的含义就变成：

如果线段树下标为 \(K\),代表线段 \([Rank[K],Rank[K+1]]\)。

下标为 \(K\) 的线段长度为 \(Rank[K+1]-Rank[K]\)

所以此时叶节点的线段长度不是 \(1\) 了。

扫描线算法函数调用部分也有所改变：

if(Line[I].In) Cover(GetRank(Line[I].y1),GetRank(Line[I].y2)-1,1,n,1);
else       Uncover(GetRank(Line[I].y1),GetRank(Line[I].y2)-1,1,n,1);