CF1528
CF1528
A: Parsa's Humongous Tree
关于这种树上的计算权值的题基本上都是树形 \(dp\).
我们先证明结论:一个数轴上有两个点,取另一个点 \(a\),点 \(a\) 在这两个点中间任意位置对距离和没有影响,但是在这两个点的左侧/右侧时,偏离的越远,距离之和越大。
这个可以推广到 \(n\) 个点,因此我们只需要取区间最大或最小值即可。
我们设 \(dp[x][0]\) 记录点 \(x\) 取到最小值,\(dp[x][1]\) 记录取到最大值,
则有 \(dp\) 方程:
dp[x][0]+=max(dp[y][0]+abs(l[y]-l[x]),dp[y][1]+abs(r[y]-l[x]));
dp[x][1]+=max(dp[y][0]+abs(l[y]-r[x]),dp[y][1]+abs(r[y]-r[x]));
这样处理之后就是一个简单的树形 \(dp\) 了!
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+5;
int T;
int n,l[N],r[N];
int nxt[N<<1],ver[N<<1],tot,head[N<<1];
ll dp[N][2];
void add(int x,int y){
ver[++tot]=y;nxt[tot]=head[x];head[x]=tot;
}
void dfs(int x,int fa){
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(y==fa) continue;
dfs(y,x);
dp[x][0]+=max(dp[y][0]+abs(l[y]-l[x]),dp[y][1]+abs(r[y]-l[x]));
dp[x][1]+=max(dp[y][0]+abs(l[y]-r[x]),dp[y][1]+abs(r[y]-r[x]));
}
}
int main(){
cin>>T;
while(T--){
scanf("%d",&n);ll ans=0;
memset(head,0,sizeof(head));
memset(dp,0,sizeof(dp));
// for(int i=0;i<=n;i++) dp[i][0]=dp[i][1]=0;
for(int i=1;i<=n;i++) scanf("%d%d",&l[i],&r[i]);
for(int i=1,x,y;i<n;i++) scanf("%d%d",&x,&y),add(x,y),add(y,x);
dfs(1,0);
printf("%lld\n",max(dp[1][1],dp[1][0]));
}
// system("pause");
return 0;
}
B: Kavi on Pairing Duty
观察样例,我们发现:
- 让不等大的圆弧都包含,有且仅有一种情况,使得中间空出空间。
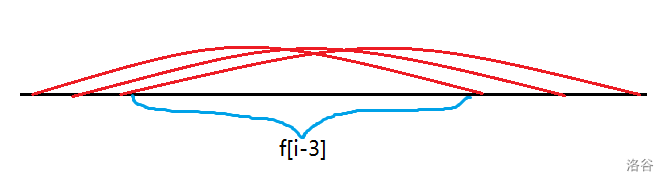
此时我们就不用管中间在干嘛,因为一定包含了,没有后效性。
- 分成了很多块,不能放东西,必须填满。
因此一个块的大小一定能整除 \(n\)。
所以可以列出 \(dp\) 方程,我们设 \(f_i\) 表示 \(2i\) 个点的答案:
预处理 \([1-n]\) 的每个数的约数个数即可,\(f[1]=1\)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
int n,dp[10000005];
signed main(){
cin>>n;
for(int i=1;i<=n;i++) for(int j=i;j<=n;j+=i) ++dp[j];
dp[1]=1;
for(int i=2;i<=n;i++) dp[i]=((dp[i-1]<<1)+dp[i])%mod;
cout<<(dp[n]-dp[n-1]+mod)%mod<<endl;
// system("pause");
return 0;
}
C:Trees of Tranquillity
我们进行讨论:
最大个数就是叶子结点个数。假设当前维护了一个叶子结点集 \(S\),新加入的结点为 \(y\)。
只有 \(∀u∈S\) ,\(x\) 既不是 \(y\) 的祖先也不在 \(y\) 的子树中,\(y\) 才可以被加入到 \(S\)中。
若 \(y\) 在 \(x\) 的子树中,用 \(y\) 替换 \(x\) 一定是最优的,所以加点策略如下:
-
若 \(y\) 是 \(x\) 的祖先,忽略 \(y\)
-
若 \(y\) 在 \(x\) 的子树中,用 \(y\) 替换 \(x\)
-
否则,将 \(y\) 加入 \(S\) 中。
如何判断 \(y\) 和 \(x\) 的关系,可以在预处理一个 \(st_i\) 和 \(ft_i\),分别代表 \(dfs\) 过程中第一次访问 \(i\) 点的时间和最后一次访问的时间,那么 -
若 \(y\) 是 \(x\) 的祖先,\(st_v≤st_u,ft_v≥ft_u\)。
-
若 \(y\) 在 \(x\) 的子树中,\(st_v≥st_u,ft_v≤ft_u\)。
对于第一种情况,将 \({st[x],x}\) 插入集合。判断时,找到第一个(保证和 \(y\) 最近) \(st[x]≥st[y]\),再 \(check ft[x]≤ft[y]\),如果是,说明 \(y\) 是 \(x\) 的祖先。
第二种情况同理。
其实这个题用树剖也行。
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll gcd(ll a,ll b) {return b ? gcd(b,a % b) : a;}
#define INF 0x3f3f3f3f
const int N=5e5 + 10;
const double eps=1e-5;
typedef pair<int,int> PII;
int st[N],ft[N];
vector<int> np1[N];
vector<int> np2[N];
set<PII> ps;
int ans;
int ti,t,n;
void dfs1(int x,int fa) {
st[x]=++ti;
for(int y : np2[x]) {
if(y==fa) continue;
dfs1(y,x);
}
ft[x]=++ti;
}
void solve(int x,int fa) {
bool ise=false;
PII keep;
auto tar=ps.lower_bound({st[x],0});
if(tar==ps.end() || ft[x] <= ft[tar->second]) {
tar=ps.upper_bound({st[x],0});
if(tar != ps.begin()) {
tar--;
int pre=tar->second;
if(ft[x] <= ft[tar->second]) {
keep=*tar;
ps.erase(tar);
ise=true;
}
}
ps.insert({st[x],x});
}
ans=max(ans,(int)ps.size());
for(int y : np1[x]) {
if(y==fa) continue;
solve(y,x);
}
if(ps.count({st[x],x})) ps.erase({st[x],x});
if(ise) ps.insert(keep);
}
int main() {
cin >> t;
while(t--) {
cin >> n;
ps.clear();
for(int i =1;i<= n;i++) {
np1[i].clear();
np2[i].clear();
}
for(int i=2,fa;i <= n;i++) {
cin >> fa;
np1[i].push_back(fa);
np1[fa].push_back(i);
}
for(int i=2,fa;i <= n;i++) {
cin >> fa;
np2[i].push_back(fa);
np2[fa].push_back(i);
}
ti=0;
ans=0;
dfs1(1,0);
solve(1,0);
cout<<ans<<endl;
}
return 0;
}
D:It's a bird! No, it's a plane! No, it's AaParsa!
我们考虑在原图中增加 \(n\) 条边,其中第 \(i\) 条为 \((i,(i+1)\%n,1)\)。
这时,从\(x->y\) 等待 \(c\) 秒,就可以转化成:
从 \(x\) 到 \(y-c\),然后通过这些新建的边 \(c\) 次到达 \(y\).
除了第一步不能走新建的边之外,其他时刻都可以任意走,因为走一次新建的边等价于在上一次走原图的时刻多等一秒。
那么直接枚举所有源点,然后新建一个点 \(S\) 把这一个点除了新加的路径以外所有路径 \(copy\) 过去,然后正常跑 \(dijkstra\) 即可.
注意不要用堆优化,因为边特别多。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=605,M=4e5+5;
int n,m,tot1;
int head[N],nxt[M],ver[M],edge[M],tot;
ll dis[N];
bool vis[N];
void add(int x,int y,int z){
ver[++tot]=y; edge[tot]=z; nxt[tot]=head[x]; head[x]=tot;
}
int main(){
cin>>n>>m;
for(int i=1,x,y,z;i<=m;i++){
scanf("%d%d%d",&x,&y,&z); add(x+1,y+1,z);
}
tot1=tot;
for(int i=1;i<=n;i++){//枚举点
memset(vis,0,sizeof(vis)); memset(dis,0x3f3f3f3f,sizeof(dis));
head[n+1]=-1,dis[n+1]=0;tot=tot1;
for(int j=head[i];j;j=nxt[j]) add(n+1,ver[j],edge[j]);
for(int j=1;j<=n;j++){
int k=0;
for(int l=1;l<=n+1;l++) if(!vis[l]&&(!k||dis[l]<dis[k])) k=l;
vis[k]=1;
for(int l=head[k];l;l=nxt[l]){
int v=(ver[l]+dis[k]-1)%n+1;//新建的点
dis[v]=min(dis[v],dis[k]+edge[l]);
}
if(k<=n) dis[k%n+1]=min(dis[k%n+1],dis[k]+1);
}
dis[i]=0;
for(int j=1;j<=n;j++) printf("%lld ",dis[j]); puts("");
}
// system("pause");
return 0;
}
E:
太难了,并没有什么思路....照着题解的思路写了写....
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5, MOD = 998244353;
typedef long long ll;
int n, ans, f[N], pref[N];
int C2(ll x) { return (ll)x * (x - 1) % MOD * 499122177 % MOD; }
int C3(ll x) { return (ll)x * (x - 1) % MOD * (x - 2) % MOD * 166374059 % MOD; }
int main()
{
cin >> n;
f[0] = 1; f[1] = 2; pref[0] = 1; pref[1] = 3;
for(int i = 2; i <= n; i++){
f[i] = (f[i - 1] + (ll)f[i - 1] * pref[i - 2] % MOD + C2(f[i - 1] + 1)) % MOD;
pref[i] = (pref[i - 1] + f[i]) % MOD;
}
ans = (ans + 2ll * f[n] - 1 + MOD) % MOD;
if(n >= 1) ans = (ans + 2ll * C3(f[n - 1] + 2)) % MOD;
if(n >= 2) ans = (ans + 2ll * ((ll)f[n - 1] * C2(pref[n - 2] + 1) + (ll)pref[n - 2] * C2(f[n - 1] + 1))) % MOD;
for(int i = 0; i < n; i++) ans = (ans + (ll)(f[i] + MOD - 1) % MOD * ((n - i - 1 >= 1) ? (f[n - i - 1] - f[n - i - 2] + MOD) % MOD : 0) % MOD) % MOD;
cout << ans << endl;
return 0;
}



