P3829 [SHOI2012]信用卡凸包

P3829 [SHOI2012]信用卡凸包

这题是个非常好的用来练手凸包的题目。

题意：

给定几个旋转后的顶点是半径为 \(r\) 的类似矩形，让你求出能包含所有矩形的多边形的边长。

解题思路：

一眼就是凸包问题，关键是怎么转换成正常的凸包。

我们从第三个样例开始分析：

首先可以做出来图：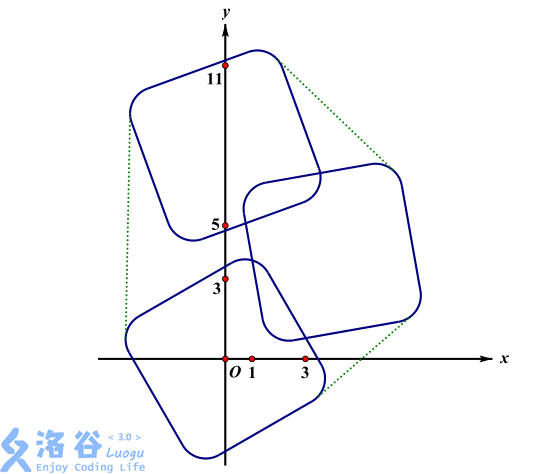

然后进一步画图：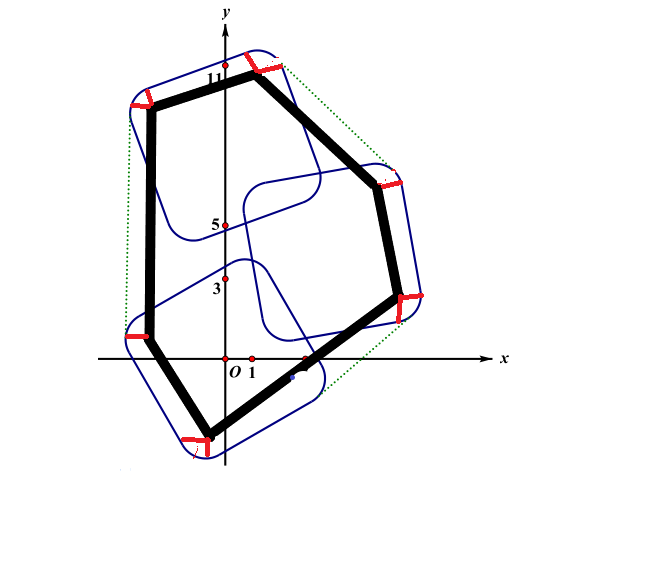

发现什么没有？

我们求的这个多边形可以转化成一个没有圆角边的多边形加上一个圆周长的长度。

为什么是半径为 \(r\) 的圆的周长？ 废话，因为你这个图形是一个周，你需要的圆自然是一个完整的圆的周长。

于是，我们便有了做法：

做法：

将圆角矩形的四个类似顶点(就是距离圆弧上所有点为r的点) 加入队列中，然后求凸包，最后加上圆的周长即可。

当然，这道题还带有旋转之类的，都是凸包的常见知识。

求顶点代码：

inline Point turn_P(Point a,ld theta){//以0为圆心顺时针旋转theta弧度
    ld x=a.x*cos(theta)-a.y*sin(theta);
    ld y=a.x*sin(theta)+a.y*cos(theta);
    return Point(x,y);
}
......
Point now=Point(x,y);
p[++cnt]=turn_P(Point(a-r,b-r),theta)+now;
p[++cnt]=turn_P(Point(r-a,b-r),theta)+now;
p[++cnt]=turn_P(Point(r-a,r-b),theta)+now;
p[++cnt]=turn_P(Point(a-r,r-b),theta)+now;

求凸包用\(Graham\)扫描法:

inline int dcmp(ld a){return a<-eps?-1:(a>eps?1:0);}//处理精度
db Cro(Point a,Point b){return a.x*b.y-a.y*b.x;}//叉积

·····

sort(p+1,p+cnt+1); 
int T=0;
for(int i=1;i<=cnt;++i){//下凸包
    while(T>1&&dcmp(Cro(p[q[T]]-p[q[T-1]],p[i]-p[q[T-1]]))<=0)--T;
    q[++T]=i;
}
int St=T;
for(int i=cnt-1;i>=1;--i){//上凸包
    while(T>St&&dcmp(Cro(p[q[T]]-p[q[T-1]],p[i]-p[q[T-1]]))<=0)--T;
    q[++T]=i;
}
double ans=2*Pi*r;
for(int i=1;i<T;i++) ans+=calc(p[q[i]]-p[q[i+1]]);

基本上就是完整代码了。