王道数据结构 （8） 树的遍历算法及递归代码实现

 

 

 

 

 

 

 

 

 

 

这 3 种顺序 是按照 跟节点的 访问顺序来的 跟节点什么时候被访问 决定了 它是哪个遍历方式 

 

 

 

 

 

 

 

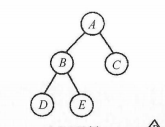
1.先序 ：  A --> B -->D-->E-->C

 

A是跟节点 BDE 是左节点 C是右节点 

 

2.中序： 左中右 

 

              D-->B-->E-->A-->C

 

BDE是左节点 A是中节点 C是右节点 

 

3.后序

左右中 

 

D-->E-->B-->C--A

 

例子： 标准树

 

 

 

代码实现：

#include<stdio.h>

/*
* 二叉树的前序、中序、后序、层序遍历演示DEMO
*/
#include <stdio.h>

typedef struct {
    char data;//数据区域(为了保存ABCD，直接用char当做数据域，便于和文章中的插图对应，稳！)
    struct BinaryTreeNode* left;//左子节点
    struct BinaryTreeNode* right;//右子节点
}BinaryTreeNode;

//为树的当前节点添加左子节
int addLeftChild(BinaryTreeNode* curNode, char leftData)
{
    //分配新节点?
    BinaryTreeNode* leftNode = (BinaryTreeNode*)malloc(sizeof(BinaryTreeNode));
    //为新节点挂载数据
    leftNode->data = leftData;
    //新节点暂时无子节点?
    leftNode->left = NULL;
    leftNode->right = NULL;
    //将新节点挂到当前节点点?
    curNode->left = leftNode;
    return 1;
}

//为树的当前节点添加右子节点?
int addRightChild(BinaryTreeNode* curNode, char rightData)
{
    //分配新节点?
    BinaryTreeNode* rightNode = (BinaryTreeNode*)malloc(sizeof(BinaryTreeNode));
    //为新节点挂载数据
    rightNode->data = rightData;
    //新节点暂时无子节点?
    rightNode->left = NULL;
    rightNode->right = NULL;
    //将新节点挂到当前节点点?
    curNode->right = rightNode;
    return 1;
}


// 前序遍历，根--点?--点?
void preOrder(BinaryTreeNode *node)
{

    if (node == NULL) {
        return;
    }
    printf("%c ", node->data);
    preOrder(node->left);
    preOrder(node->right);
}

// 中序遍历，左--点?--点?
void midOrder(BinaryTreeNode *node)
{

    if (node == NULL) {
        return;
    }
    midOrder(node->left);
    printf("%c ", node->data);
    midOrder(node->right);
}


// 后序遍历，左--点?--点?
void afterOrder(BinaryTreeNode *node)
{

    if (node == NULL) {
        return;
    }
    afterOrder(node->left);
    afterOrder(node->right);
    printf("%c ", node->data);
}


//----------------------------------------------------------------------------------------------------测试入口区域
int main()
{
    //设定根节点?
    BinaryTreeNode root;
    //根节点A
    root.data = 'A';
    addLeftChild(&root, 'B');
    addRightChild(&root, 'C');
    //为B节点增加子节点?
    addLeftChild(root.left, 'D');
    addRightChild(root.left, 'E');
    //为C节点增加子节点?
    addLeftChild(root.right, 'F');
    addRightChild(root.right, 'G');
    printf("\n前序遍历：");
    preOrder(&root);
    printf("\n中序遍历：");
    midOrder(&root);
    printf("\n后序遍历：");
    afterOrder(&root);

    return 1;
}

输出：

 

 

 

 

 

前序遍历 运行过程：

 

1.传入跟节点  输出 A 

 

 preOrder（）

 执行 

2.遍历 B 节点 B树里面包含 D和 E   

  preOrder(node->left); 执行   

 

 里面又遍历了一遍   

 preOrder(node->left);
  preOrder(node->right);

 

3.遍历C节点 节点 包含 F 和 G 

 preOrder(node->right); 执行   

 

里面又遍历了一遍   

 preOrder(node->left);
  preOrder(node->right);

 

 

其他两种遍历方式的思路跟前序遍历是一样的