几种简易测地球周长或半径的方法
在学万有引力定律的时候，我们一直感叹在那个还没有精确仪器的年代，古人居然已经凭借观测和几何就已经测出了地球的半径、月地距离、日地距离，这是多么了不起的成就和智慧。时至今日我们的很多人居然还只是处于闻听而不知其理的阶段，很多人甚至包括物理教学工作者依然不解其中道，这不能不说是令人多么的遗憾。网上有大量相关资料和信息，但大多数仅仅限于历史介绍，对于原理的关键点却避之不谈，仅有的几篇却又显得高冷复杂，拒人千里之感。正因如此，接下来的几篇文章费了笔者大量心血搜集资料、改编整理，如何把这其中的道理讲得浅显易懂，让人人都看得懂、理得清，这是我所追求的。
一、古希腊的三角测量法
2000多年前,就有人用简单的测量工具计算出地球的周长.这个人就是古希腊的埃拉托色尼(约公元前275—前194)。
埃拉托色尼博学多才,他不仅通晓天文,而且熟知地理；又是诗人、历史学家、语言学家、哲学家,曾担任过亚历山大博物馆的馆长.
细心的埃拉托色尼发现：离亚历山大城约800公里的塞伊城(今埃及阿斯旺附近),夏日正午的阳光可以一直照到井底,因而这时候所有地面上的直立物都应该没有影子。但是,亚历山大城地面上的直立物却有一段很短的影子。他认为：直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。
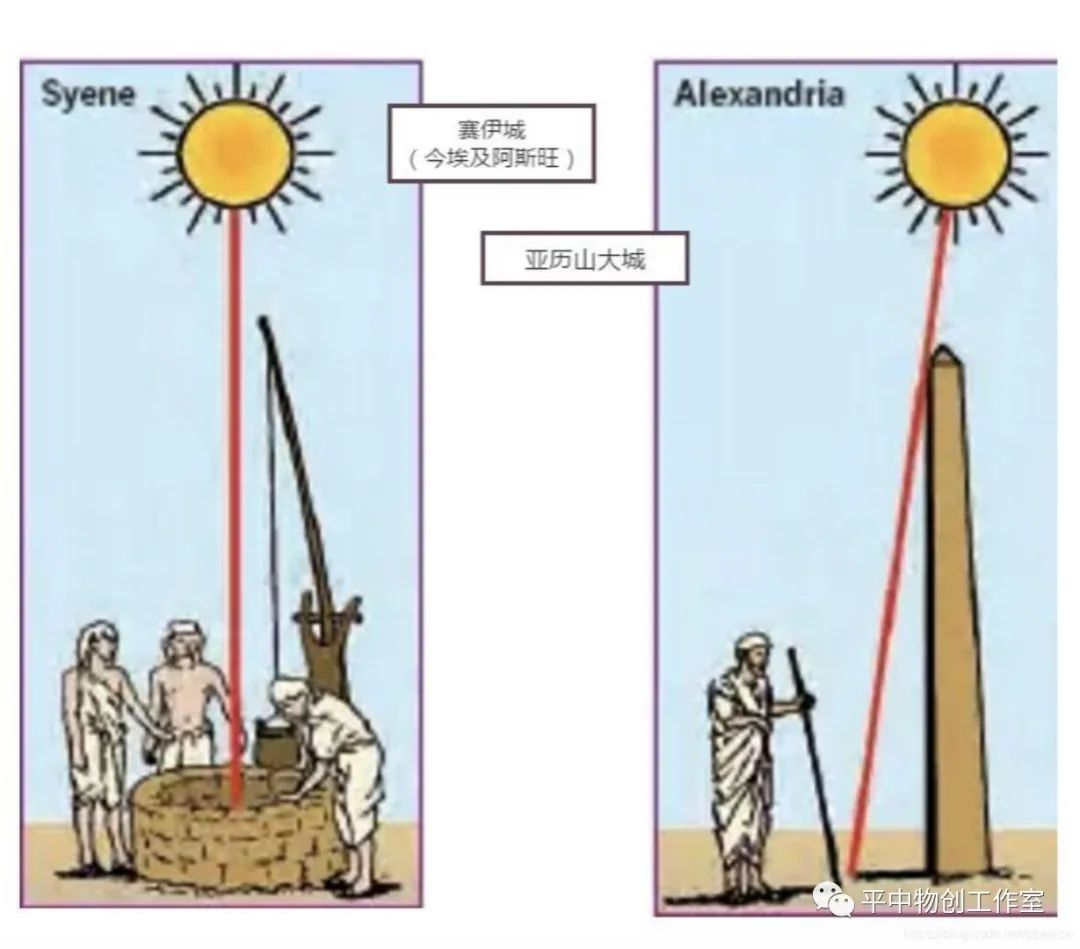
从地球是圆球和阳光直线传播这两个前提出发,从假想的地心向塞伊城和亚历山大城引两条直线,其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。
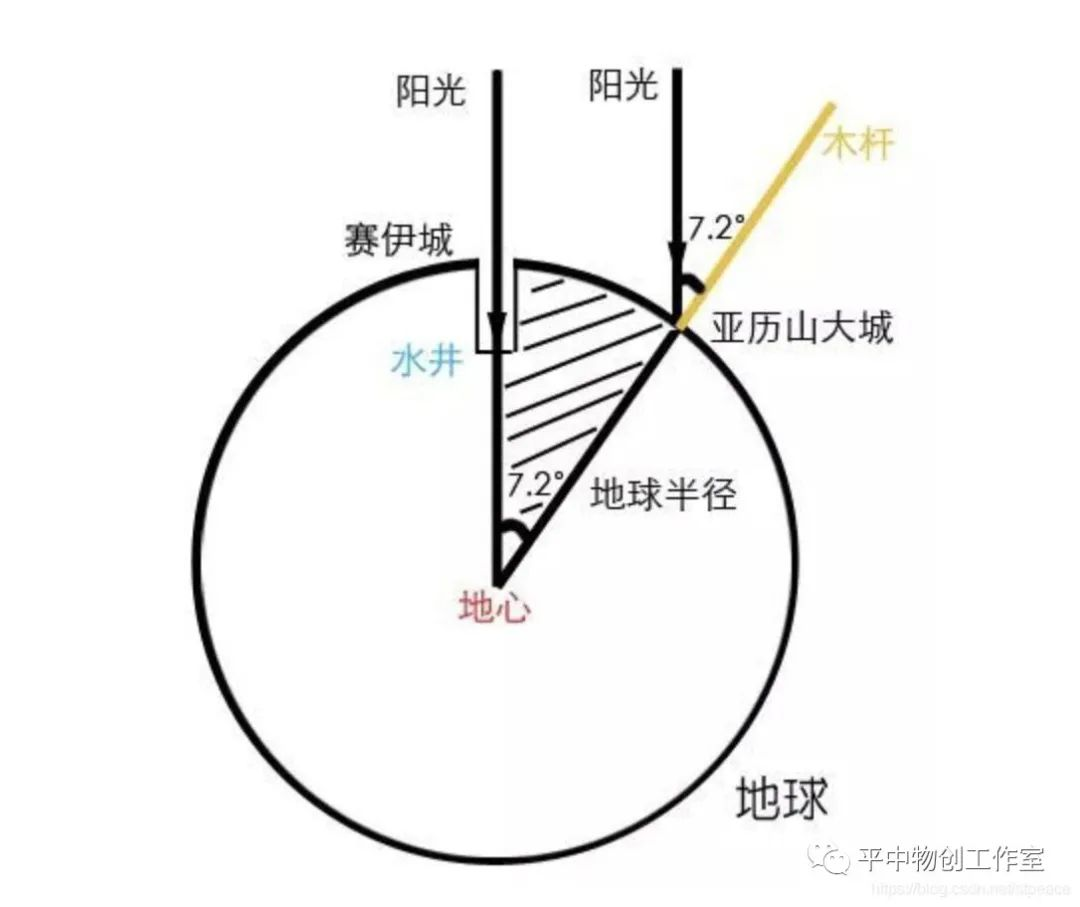
埃拉托色尼测出夹角约为7度，这个角度可以通过测杆的长度和影子的长度得出，结果是地球圆周角(360度)的五十分之一,再测出压力山大城和赛伊城的距离Ｌ，则地球的周长S：
S=（360/7）L
又知L约为5000古希腊里，他按照弧长与圆心角的关系，算出了地球的半径约为4000古希腊里。一般认为1古希腊里约为158.5米，那么他测得地球的半径约为6340公里,由此推算地球的周长大约为4万公里,这与实际地球周长(40076公里)相差无几。他还算出太阳与地球间距离为1.47亿公里,和实际距离1.49亿公里也惊人地相近。这充分反映了埃拉托色尼的学说和智慧。
二、近代测量方法
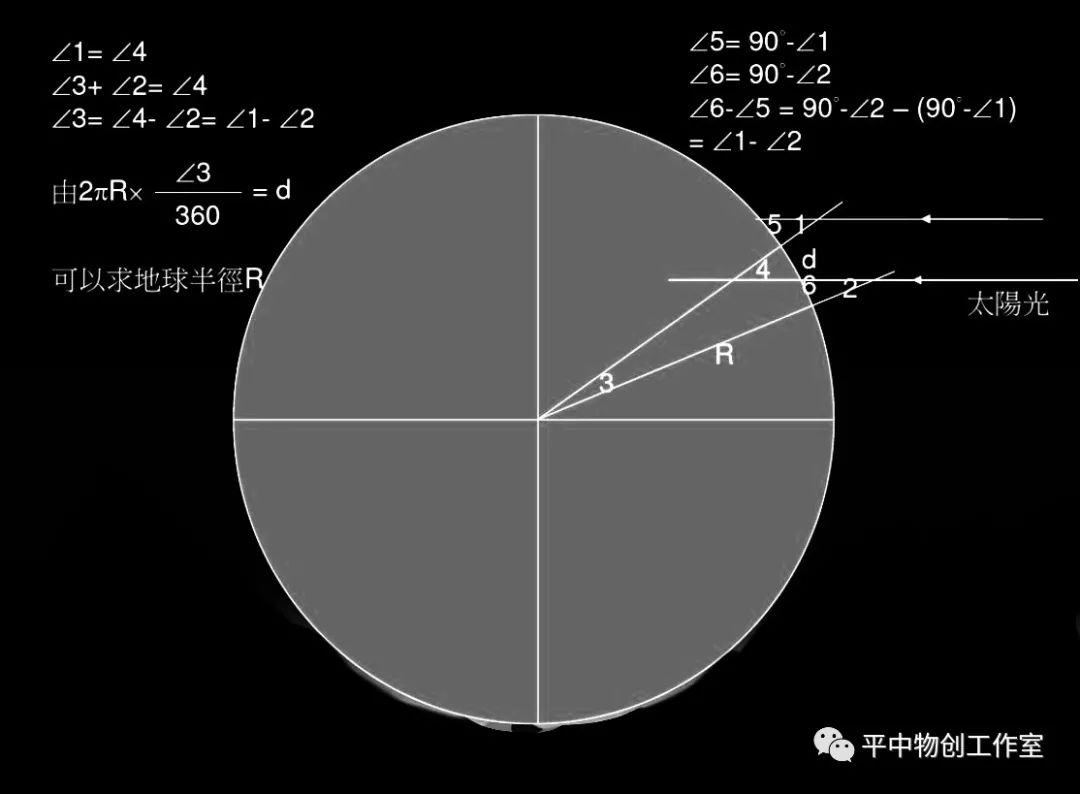
近代测量地球的半径，还用弧度测量的方法。我们认为太阳光是平行光，如能测出两地之间的距离和对应的地心角，便可算出地球半径。如下图所示，大家可以约上两个好友在同一经度的两个较远地方测量这两个地方的地心夹角。（井老师偷偷告诉你一个简易的办法，角1和角2可以用悬挂单摆法测，测出摆长和水平影子的长度就可求出，再利用下图中的推导就可求出两地地心夹角3
只是在求相距很远的两地间的距离时，采用了布设三角网的方法。比如求M、N两地的距离时，可以像下图那样布设三角点，用经纬仪测量出△AMB，△ABC，△BCD，△CDE，△EDN的各个内角的度数，再量出M点附近的那条基线MA的长，最后即可算出MN的长度了。
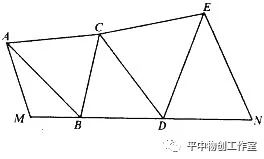
通过这些三角形，怎样算出MN的长度呢?这里要用到三角形的一个很重要的定理——正弦定理。即：在一个三角形中，各边和它所对角的正弦的比相等。在图上中，由于各三角形的内角已测出，AM的长也量出，由正弦定理即可分别算出：
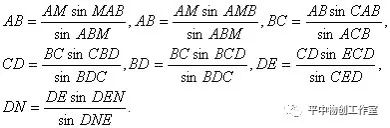
∴MN=MB+BD+DN。
在结合M、N两地对应的地心角就可计算地球半径了。
三、海边看日出
如果用这种方法，你需要做如下准备：带一块秒表、量一下你的身高、上好闹钟，当然还得找个海边。起个大早，站在海边看日出，当刚刚看到太阳的时候，开始计时，并且马上趴到地上；这个时候你会发现看不到太阳了，等再一次看到太阳的时候，停止计时。然后就可以算地球的半径了。
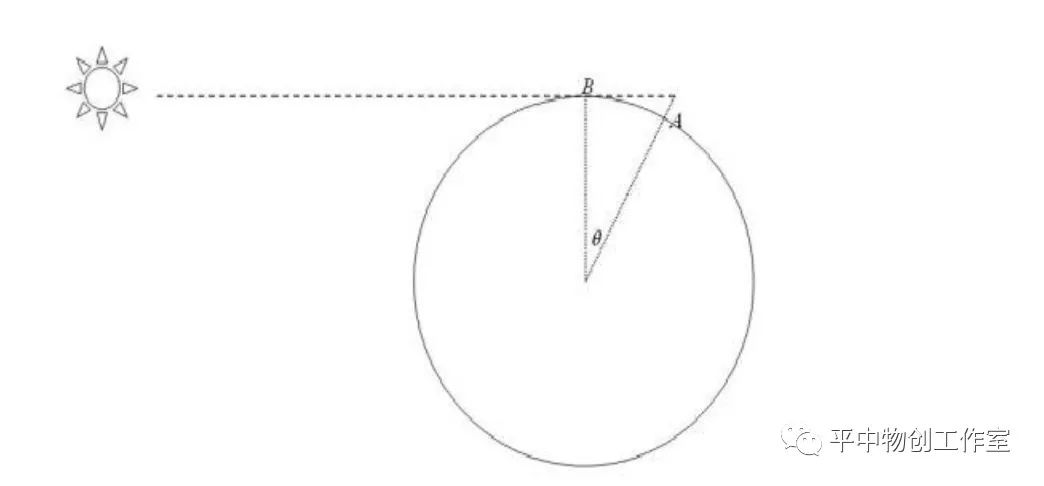
你站在海边，太阳光穿过地平线到达你的眼睛，此时你的位置是在A点，高出地球的那段距离就是你的身高；趴到地上后，由于高度变低，所以你看不到太阳了，当地球自转使你到达B点后，你才能重新看到太阳，在这个过程中地球转过的角度是我们知道，地球一天转一圈，所以
θ=360°xt+24小时
其中t是你的秒表测量出的时间。另外根据几何关系
(R+h)cosθ=R
可以得出地球半径
R=h cosθ / (1-cosθ)
式中h是你的身高。根据上面2个公式，可以很简单的估算出地球的半径。
不过，你真去测量的时候，会发现算出来的结果与实际情况差别较大。实际上，上面的方法只适用于在赤道上测量，当你在地球的其他地方测量时，测出的是当地纬度圈的半径。考虑到黄赤交角(地球自转轨道和地球公转轨道之间的夹角)的影响，我们用上述方法测量出的结果在不同的季节还要做适当的修正。
四、一张照片测地球半径
你相信吗，仅仅利用一张日落的照片，你就能得出地球的半径大小！ 国外某大学教授在一篇论文中对一张摄于密歇根湖的日落照片进行了分析，不但证实了地球是圆的，还依据照片上的内容对地球半径进行了估算。在这里把他的计算的大致过程向大家描述一下，供大家膜拜。
事情的起因就是上面这张很平常的日落照片，以及这样一个大家平时并没有太在意的问题：太阳露出水面的部分应该是一个标准的弓形，但为什么在日出日落时，我们所看到的太阳是一个橄榄球一样的形状？大家或许会很快想到，发光体的下半部分其实是日光反射在水面上造成的。随之产生的是另一个问题：为什么它的下半部分要比上半部分小一些呢？
原因在于这里，下图就是人站在地球上看日出的一个比例夸张版示意图，其中 O 为地球的中心， A 为人眼的位置， AB 为视平线， B 点为水天交界处。由于太阳距离我们相当遥远，因此我们把太阳光看作是一束理想的平行光线。我们把直接射入人眼的太阳光与 AB 的夹角记为 α ，把经过水面上的一点 C 反射进入人眼的光线与 AB 的夹角记为 β 。从图上可见，视角 β 比 α 小，也就是说太阳在水面上的镜像比本身要小一些。
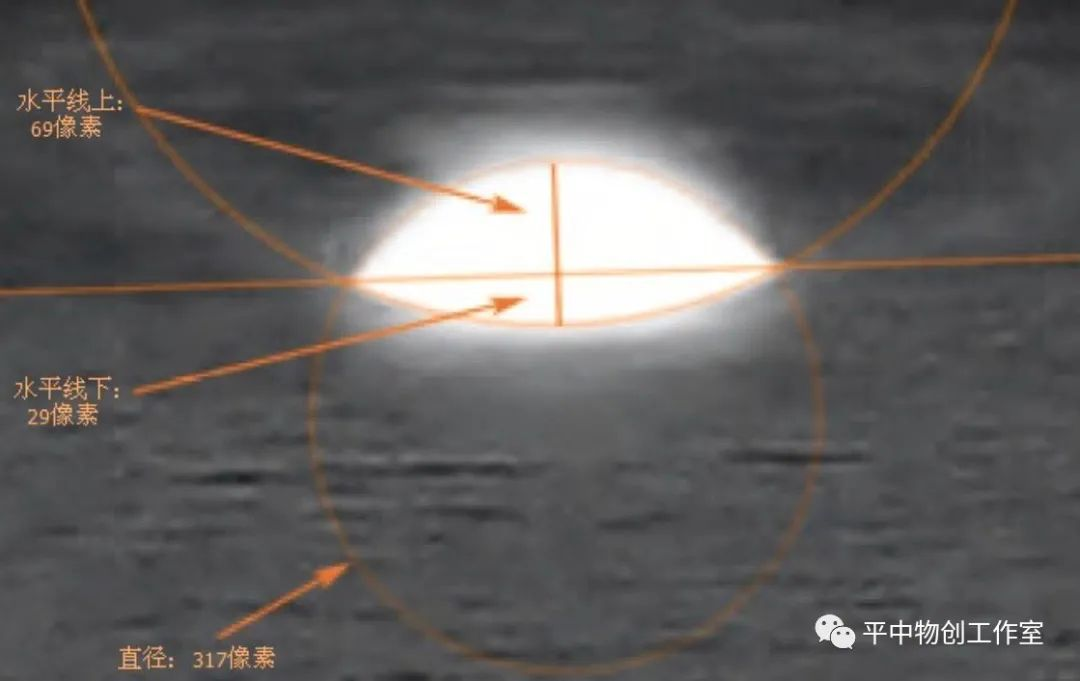
β 究竟比 α 小多少呢？对照片进行精确地测量，可知太阳的直径相当于照片中的 317 个像素，而露出水面的部分高 69 像素，水中的倒影则只有 29 像素。众所周知太阳的视直径（看太阳的视角）为 0.5 度，因此我们就得到 α = 0.5 * 69 / 317 ≈ 0.1088 度， β = 0.5 * 29 / 317 ≈ 0.0457 度。
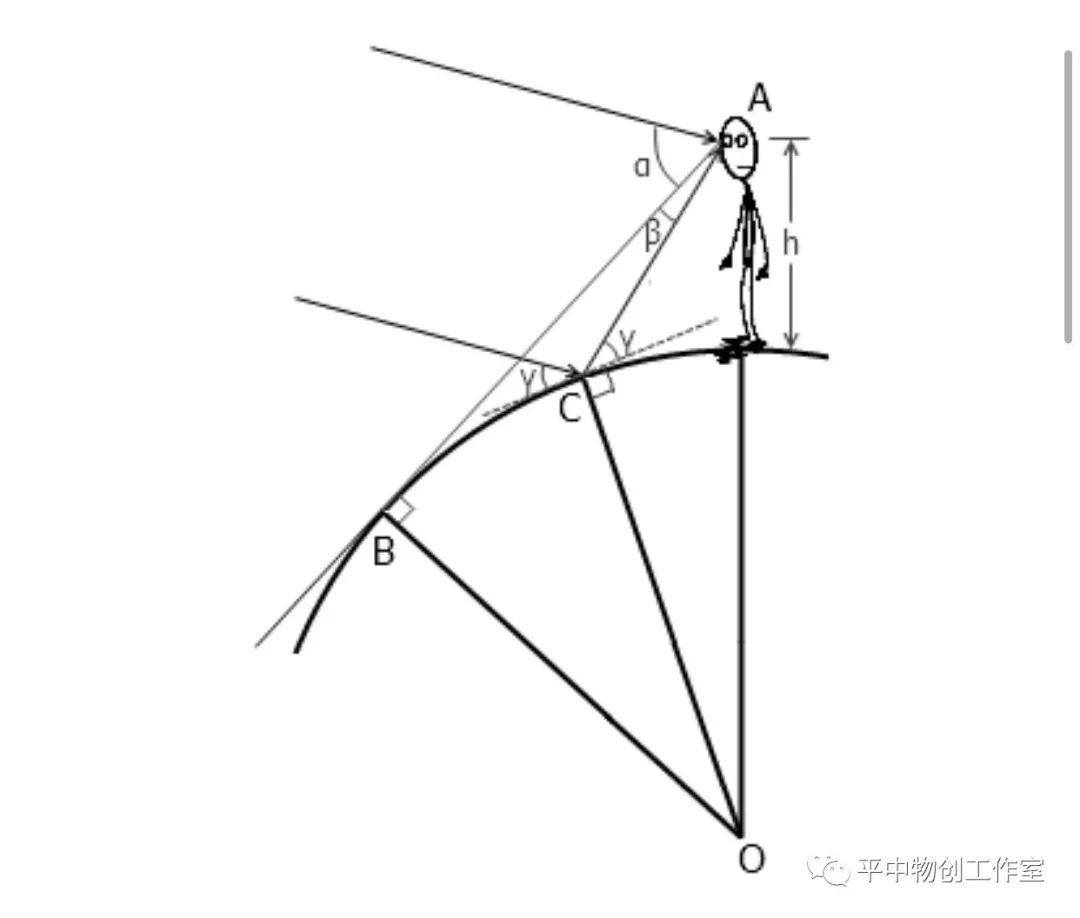
如果再已知人眼（或者说相机）离水面的垂直距离 h 为 2 米，那么根据这些数据我们就足以估算出地球的半径了。不妨把 ∠AOB 记为 φ ，把 ∠AOC 记为 θ ，把人眼到水天相接处的距离 AB 记为 D ，把人眼到反射点的距离 AC 记为 d ，入射角和反射角记为 γ ，最后用 r 来表示地球半径，那么此时我们一共有 6 个未知量。
为了求解出这 6 个未知数，我们需要寻找 6 个不同的方程。这 6 个方程可以由以下 6 组等量关系得到：
1.四边形OBAC的内角和为360°， 即
(φ-θ)+90°+β+(180°-γ+90°)=360°
化简得方程
(1) φ+β=θ+γ
2.两条平行线的同旁内角相加为180°
(α+β)+(180°-2y)=180°，
即方程
(2)α+β=2y
3.由于AO=h+r，同时又有
AO=AD+DO=D·sinφ+r·cosφ
因此有方程
(3)h+r=D·sind+r·cosφ
4.BD既等于D·cosφ还等于rsinφ，所以有方程
(4)D·cosφ=r•sinφ
5.由于AO=h+r，同时又有.
AO=AE+EO=d·sin(θ+γ)+ rcosθ
因此有方程
(5)h+r=d·sin(θ+γ)+ rcosθ
6.CE既可以等于d·cos(θ+γ)又可以等于r·sinθ
于是有方程
(6)d·cos(θ+γ)=r·sinθ
通过以上六个方程式进行一系列代数运算最终可得地球半径r。
当然，地球并非是一个圆球体，而是一个椭球体，现代科学可以利用卫星高精度测量地球周长和半径，但是那些古老的方法和简易的办法中体显出人类的智慧依然值得我们学习和借鉴。
