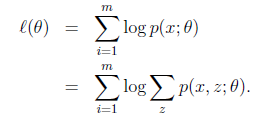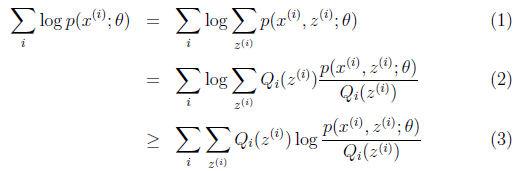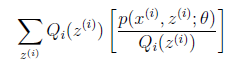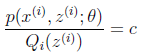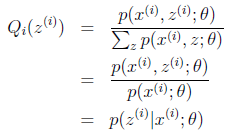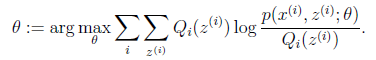EM算法原理及证明

EM算法原理及证明

1、EM算法

     最大期望（EM）算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量。

     给定的训练样本是，样例间独立，我们想找到每个样例隐含的类别z，能使得p(x,z)最大。p(x,z)的最大似然估计如下：

               

  　第一步是对极大似然取对数，第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求一般比较困难，因为有隐藏变量z存在，但是一般确定了z后，求解就容易了。EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化，我们可以不断地建立的下界（E步），然后优化下界（M步）。

     对于每一个样例i，让表示该样例隐含变量z的某种分布，满足的条件是。（如果z是连续性的，那么是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了。

    可以由前面阐述的内容得到下面的公式：

             

（2）到（3）利用了Jensen不等式，考虑到是凹函数（二阶导数小于0），而且

            

      就是的期望

这个过程可以看作是对求了下界。对于的选择，有多种可能，那种更好的？假设已经给定，那么的值就决定于和了。我们可以通过调整这两个概率使下界不断上升，以逼近的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的概率能够等价于了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：

            

      c为常数，不依赖于。对此式子做进一步推导，我们知道，那么也就有，（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），那么有下式：

            

      至此，我们推出了在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。这一步就是E步，建立的下界。接下来的M步，就是在给定后，调整，去极大化的下界（在固定后，下界还可以调整的更大）。

　对于一般的EM算法步骤：

　　（1）、E步：对于每一个i，计算

  　 　　　

　　（2）、M步：计算

           

 参考文献：（EM算法）The EM Algorithm