最近在学习椭球拟合,最小二乘(加速度)的相关内容,把不错的几个学习参考链接放到下面:
三维空间中的椭球拟合与磁力计、加速度计校正
最小二乘估计及证明
平面二维任意椭圆数据拟合算法推导及程序实现详解
空间二次曲面数据拟合算法推导及仿真分析
IMU加速度、磁力计校正--椭球拟合
附上通过学习以上文章写出的测试代码;
%最小二乘的方法进行拟合
clear all;
close all
clc;
R = 2; %球面半径
RX = 2;
RY = 10;
RZ = 20;
x0 = 100; %球心x坐标
y0 = 1; %球心y坐标
z0 = 76; %球心z坐标
alfa = 0:pi/50:pi;
sita = 0:pi/50:2*pi;
num_alfa = length(alfa);
num_sita = length(sita);
x = zeros(num_alfa,num_sita);
y = zeros(num_alfa,num_sita);
z = zeros(num_alfa,num_sita);
for i = 1:num_alfa
for j = 1:num_sita
x(i,j) = x0+RX*sin(alfa(i))*cos(sita(j));
y(i,j) = y0+RY*sin(alfa(i))*sin(sita(j));
z(i,j) = z0+RZ*cos(alfa(i));
end
end
x = reshape(x,num_alfa*num_sita,1);
y = reshape(y,num_alfa*num_sita,1);
z = reshape(z,num_alfa*num_sita,1);
figure;
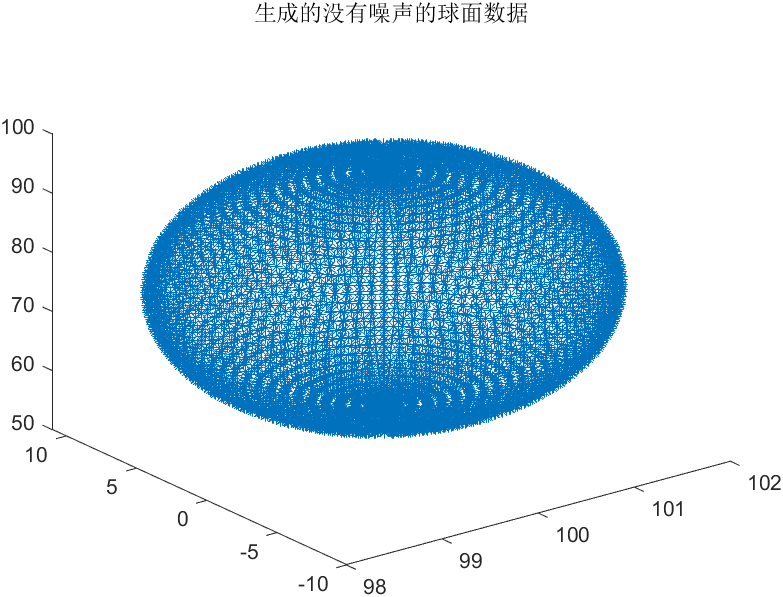
plot3(x,y,z,'*');
title('生成的没有噪声的球面数据');
%加入均值为0的高斯分布噪声
amp = 1;
x = x + amp*rand(num_alfa*num_sita,1);
y = y + amp*rand(num_alfa*num_sita,1);
z = z + amp*rand(num_alfa*num_sita,1);
figure;
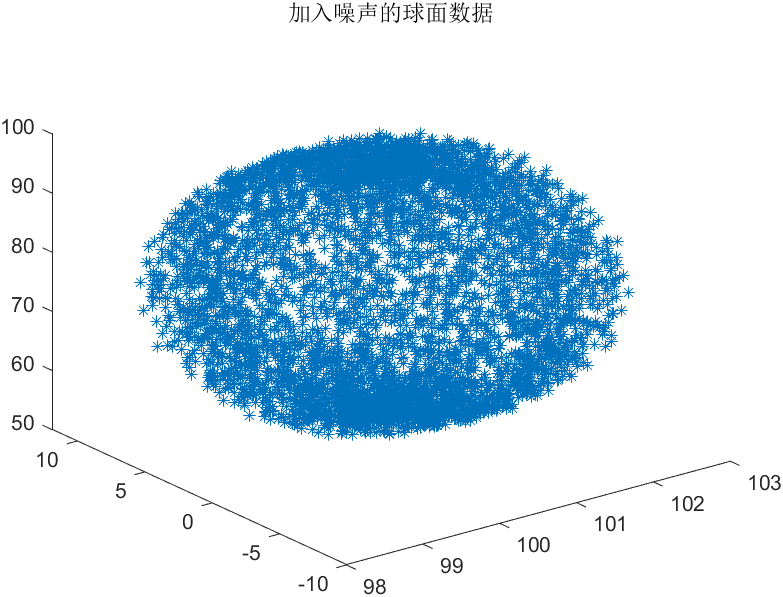
plot3(x,y,z,'*');
title('加入噪声的球面数据');
x;
y;
z;
K = [y.^2 z.^2 x y z ones(length(x),1)];
% x2=x.^2;
% y2=y.^2;
% z2=z.^2;
%
% K = [ y2(1,1) z2(1,1) x(1,1) y(1,1) z(1,1) 1 ;
% y2(10,1) z2(10,1) x(10,1) y(10,1) z(10,1) 1 ;
% y2(20,1) z2(20,1) x(20,1) y(20,1) z(20,1) 1 ;
% y2(21,1) z2(21,1) x(21,1) y(21,1) z(21,1) 1 ;
% y2(49,1) z2(49,1) x(49,1) y(49,1) z(49,1) 1 ;
% y2(100,1) z2(100,1) x(100,1) y(100,1) z(100,1) 1 ]
Y = [-x.^2];
% Y = [ -x2(1,1);
% -x2(10,1);
% -x2(20,1);
% -x2(21,1);
% -x2(49,1);
% -x2(100,1);]
KT = K.';
X=inv(KT*K)*KT*Y;
RA = X(1,1);
RB = X(2,1);
RC = X(3,1);
RD = X(4,1);
RE = X(5,1);
RF = X(6,1);
disp("椭球原始数据")
x0
y0
z0
RX
RY
RZ
disp("解出来的椭球数据")
OX= -RC/2
OY=-RD/2/RA
OZ=-RE/2/RB
FRX=sqrt(OX^2+RA*OY^2+RB*OZ^2-RF)
FRY=sqrt(FRX^2/RA)
FRZ=sqrt(FRX^2/RB)
=========================>>
=========================>>
=========================>>






