CF #487 (Div. 2) D. A Shade of Moonlight 构造_数形结合

题意：
给 $n$个长度为 $l$ 且互不相交的开区间 $(x_{i}, x_{i}+l)$ ，每个区间有一个移动速度 $v$，$v∈1,-1$。你可以在某一时刻给所有区间同时增加一个速度 $w$，要求满足 $|w|<= w_{max}$
求有对多少对 $(i,j)(i<j)$ 移动的过程中能同时覆盖原点（坐标为 $0$ 的点）。
数据·范围：
( $n<=10^5$) ($l,w_{max}<=10^8$).

看图说话：

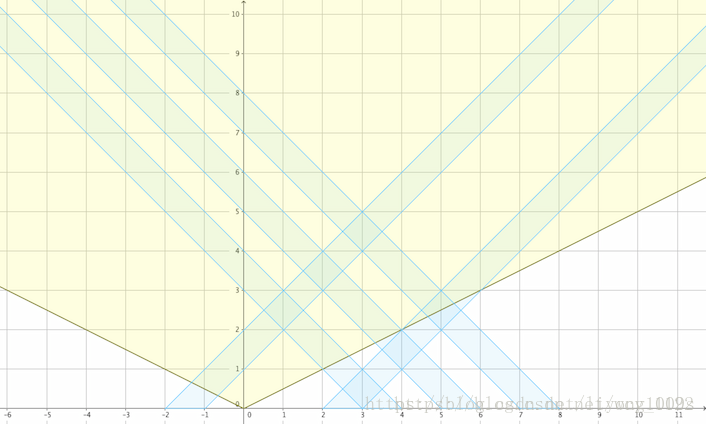
我们设图中的横坐标为原坐标系中的横坐标，纵坐标代表时间。

蓝色柱子代表一个区间所覆盖的轨迹，黄色区域为原点移动所能覆盖的地方。

显然，两个区间的相互重叠部分与原点重合当且仅当两个蓝色柱子在黄色区域处有公共部分。

我们可以将所有区间分为2类，1.速度为1，即向右移动的区间。2.速度为-1，即向左移动的区间，并分别将这些区间排序，依次枚举向右移动的区间，在向左移动的区间中进行二分。因为 $w_{max}>=1$，所以我们要找到一个符合要求的初始横坐标最小的一个。至于如何判断任意两条蓝柱和黄色区域是否有交点，我们只需拿出两条蓝色柱子最靠外的两条直线，求交点，并将交点的横坐标带入到黄色区域边缘的直线上，看带而得出的纵坐标的大小是否小于等于带入求出的蓝线交点的纵坐标即可。时间复杂度为$O(nlogn)$