luogu P1856 [USACO5.5]矩形周长Picture 扫描线 + 线段树（扫描线讲解）

题目背景

墙上贴着许多形状相同的海报、照片。它们的边都是水平和垂直的。每个矩形图片可能部分或全部的覆盖了其他图片。所有矩形合并后的边长称为周长。

题目描述

编写一个程序计算周长。

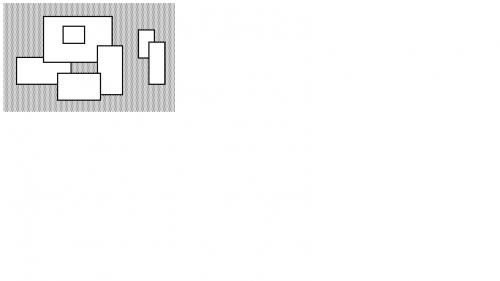
如图1所示7个矩形。

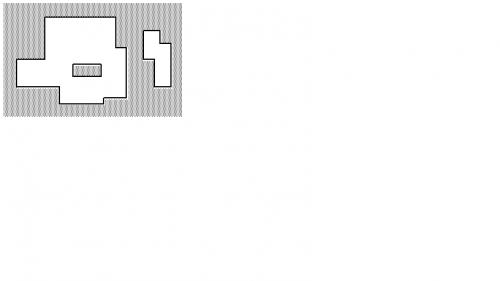
如图2所示，所有矩形的边界。所有矩形顶点的坐标都是整数。

输入输出格式

输入格式：

 

输入文件的第一行是一个整数N（0<=N<5000），表示有多少个矩形。接下来N行给出了每一个矩形左下角坐标和右上角坐标（所有坐标的数值范围都在-10000到10000之间）。

 

输出格式：

 

输出文件只有一个正整数，表示所有矩形的周长。

这里提供一种线段树实现扫描线的方法：
碰到下边就在图中投影一条线段，遇到上边就在图中删除一条线段.
对于每个节点，我们维护这几个值：
$numv[o],len[o],lflag[o],rflag[o],sumv[o]$
其中分别代表： 该区间左右端点个数，区间被覆盖总长度，线段树中左儿子是否被覆盖，线段树中右儿子是否被覆盖，该点被覆盖的 线段数目
在节点 $x$ 插入了一个线段，节点 $x$ 维护 $[l,r]$ ，直接在对应的 
$sumv[o]$ 上加上一即可，删除操作时类似的，将 $sumv[o]$ 减一就行.
考虑 $pushup$ 函数:
假设 $sumv[o]$ > 1, 说明该区间正被一个线段覆盖着，那么显然 $lflag[o]=rflag[o]=1$, $len[o]=r-l+1$.
$sumv[o]=0$，则该区间并没又有被一个完整的区间所覆盖. 
$len[o]=len[ls]+len[rs]$
$numv[o]=numv[ls]+numv[rs]$
$if(rflag[ls](and)lflag[rs])--numv[o]$
$lflag[o]=lflag[ls]$
$rflag[o]=rflag[rs]$      

#include<bits/stdc++.h>
#define maxn 200007 
#define inf 100005   
using namespace std;
void setIO(string s)
{
    string in=s+".in"; 
    freopen(in.c_str(),"r",stdin); 
}
struct Edge
{
    int l,r,h,flag; 
}edges[maxn];   
int n; 
namespace tr
{
    #define ls lson[o]
    #define rs rson[o]
    #define mid ((l+r)>>1) 
    int tot; 
    int lson[maxn<<2],rson[maxn<<2],lflag[maxn<<2],rflag[maxn<<2],sumv[maxn<<2],numv[maxn<<2],len[maxn<<2]; 
    int newnode() { return ++tot; }         
    void pushup(int o,int l,int r)
    {
        if(sumv[o]) 
        {
            numv[o]=1;                 
            len[o]=r-l+1; 
            lflag[o]=rflag[o]=1;         
        }   
        else 
        {
            len[o]=len[ls]+len[rs]; 
            numv[o]=numv[ls]+numv[rs]; 
            if(rflag[ls]&&lflag[rs]) --numv[o]; 
            lflag[o]=lflag[ls]; 
            rflag[o]=rflag[rs];                    
        }
    }
    void add(int &o,int l,int r,int L,int R,int v)
    {
        if(!o) o=newnode(); 
        if(l>=L&&r<=R)
        {
            sumv[o]+=v; 
            pushup(o,l,r); 
            return; 
        }
        if(L<=mid) add(ls,l,mid,L,R,v); 
        if(R>mid) add(rs,mid+1,r,L,R,v); 
        pushup(o,l,r);         
    }
};     
bool cmp(Edge a,Edge b)
{
    if(a.h==b.h)  return a.flag > b.flag;
    else  return a.h < b.h; 
}
int main()
{
    //  setIO("input"); 
    scanf("%d",&n); 
    int a,b,c,d,i,ed=0,j,root=0,last=0,ans=0;  
    for(i=1;i<=n;++i)
    {
        scanf("%d%d%d%d",&a,&b,&c,&d); 
        edges[++ed].l=a,edges[ed].r=c-1,edges[ed].h=b,edges[ed].flag=1;         // 加边
        edges[++ed].l=a,edges[ed].r=c-1,edges[ed].h=d,edges[ed].flag=-1;        // 删边   
    }
    sort(edges+1,edges+1+ed,cmp); 
    for(i=1;i<=ed;++i)
    {
        tr::add(root,-inf,inf,edges[i].l,edges[i].r,edges[i].flag);                                 
        ans+=abs(tr::len[root]-last);    
        last=tr::len[root]; 
        ans+=((tr::numv[root]<<1)*(edges[i+1].h-edges[i].h)); 
    }
    printf("%d\n",ans); 
    return 0; 
}