BZOJ 4817: [Sdoi2017]树点涂色 LCT + DFS序 + 线段树
Description
Bob有一棵n个点的有根树,其中1号点是根节点。Bob在每个点上涂了颜色,并且每个点上的颜色不同。定义一条路
径的权值是:这条路径上的点(包括起点和终点)共有多少种不同的颜色。Bob可能会进行这几种操作:
1 x:
把点x到根节点的路径上所有的点染上一种没有用过的新颜色。
2 x y:
求x到y的路径的权值。
3 x
在以x为根的子树中选择一个点,使得这个点到根节点的路径权值最大,求最大权值。
Bob一共会进行m次操作
Input
第一行两个数n,m。
接下来n-1行,每行两个数a,b,表示a与b之间有一条边。
接下来m行,表示操作,格式见题目描述
1<=n,m<=100000
Output
每当出现2,3操作,输出一行。
如果是2操作,输出一个数表示路径的权值
如果是3操作,输出一个数表示权值的最大值
题解:
和事情的相似度那道题挺像的.
都是利用 $LCT$ 中同一颗 $splay$ 中颜色相等这个性质.
这道题用线段树维护一下 DFS 序,查询的时候在 DFS 序中查询即可.
维护每个点到根节点的色块个数.
考虑染色时会产生的影响:
都是利用 $LCT$ 中同一颗 $splay$ 中颜色相等这个性质.
这道题用线段树维护一下 DFS 序,查询的时候在 DFS 序中查询即可.
维护每个点到根节点的色块个数.
考虑染色时会产生的影响:
假设现在要把某个点到根节点路径都染成蓝色.
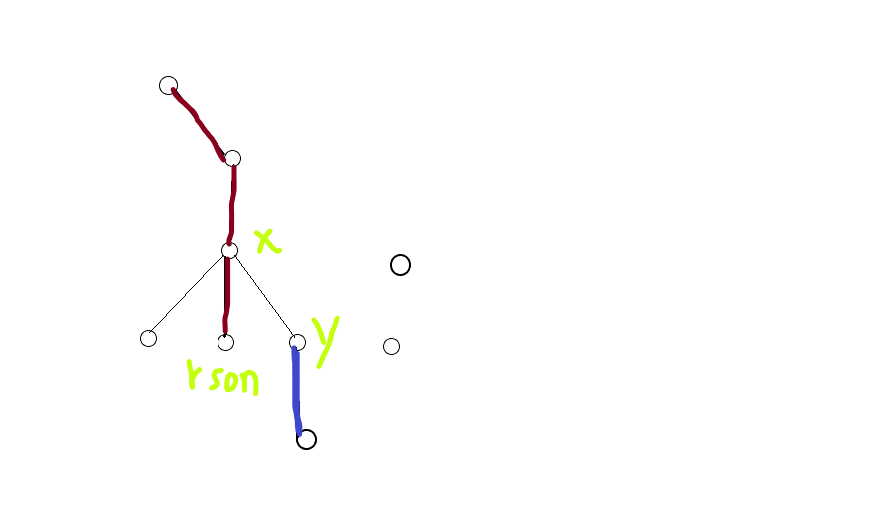
当前 $Access$ 时处理的点为 $x$,右儿子为 $rson$,要连接的为 $y$
那么,对于 $y$ 及其子树来说,原来有红 + 蓝,现在将只有蓝,答案减一
对于 $rson$ 及其子树来说,原来只有红,现在有红 + 蓝( $rson$ 没被染成蓝色)
对于子树权值修改,直接上线段树即可.
当前 $Access$ 时处理的点为 $x$,右儿子为 $rson$,要连接的为 $y$
那么,对于 $y$ 及其子树来说,原来有红 + 蓝,现在将只有蓝,答案减一
对于 $rson$ 及其子树来说,原来只有红,现在有红 + 蓝( $rson$ 没被染成蓝色)
对于子树权值修改,直接上线段树即可.
#include<bits/stdc++.h>
#define maxn 200003
#define inf -1000000
using namespace std;
void setIO(string s)
{
string in=s+".in",out=s+".out";
freopen(in.c_str(),"r",stdin);
freopen(out.c_str(),"w",stdout);
}
int tim,edges,n,Q,_curcol;
int dfn[maxn],ln[maxn],fa[maxn],hd[maxn],to[maxn<<1],nex[maxn<<1];
int st[maxn],ed[maxn],top[maxn],hson[maxn],siz[maxn],dep[maxn];
void addedge(int u,int v)
{
nex[++edges]=hd[u],hd[u]=edges,to[edges]=v;
}
namespace tr
{
int maxv[maxn<<2],lazy[maxn<<2];
void mark(int x,int k)
{
lazy[x]+=k, maxv[x]+=k;
}
void pushdown(int l,int r,int x)
{
if(!lazy[x]) return;
int mid=(l+r)>>1;
if(mid>=l) mark(x<<1,lazy[x]);
if(r>mid) mark((x<<1)|1,lazy[x]);
lazy[x]=0;
}
void update(int l,int r,int x,int L,int R,int k)
{
if(l>=L&&r<=R)
{
mark(x,k);
return;
}
pushdown(l,r,x);
int mid=(l+r)>>1;
if(L<=mid) update(l,mid,x<<1,L,R,k);
if(R>mid) update(mid+1,r,(x<<1)|1,L,R,k);
maxv[x]=max(maxv[x<<1],maxv[(x<<1)|1]);
}
int query(int l,int r,int x,int L,int R)
{
if(l>=L&&r<=R) return maxv[x];
pushdown(l,r,x);
int mid=(l+r)>>1, tmp=inf;
if(L<=mid) tmp=max(tmp,query(l,mid,x<<1,L,R));
if(R>mid) tmp=max(tmp,query(mid+1,r,(x<<1)|1,L,R));
return tmp;
}
int po(int l,int r,int x,int k)
{
if(l==r) return maxv[x];
int mid=(l+r)>>1;
pushdown(l,r,x);
if(k<=mid) return po(l,mid,x<<1,k);
else return po(mid+1,r,(x<<1)|1,k);
}
};
namespace tree
{
#define lson ch[x][0]
#define rson ch[x][1]
#define get(x) (ch[f[x]][1]==x)
#define isrt(x) (!(ch[f[x]][0]==x||ch[f[x]][1]==x))
int ch[maxn][2],f[maxn],col[maxn],sta[maxn];
void pushdown(int x)
{
if(!x) return;
if(col[x])
{
if(lson) col[lson]=col[x];
if(rson) col[rson]=col[x];
}
}
int findrt(int x)
{
while(lson)x=lson;
return x;
}
void rotate(int x)
{
int old=f[x],fold=f[old],which=get(x);
if(!isrt(old)) ch[fold][ch[fold][1]==old]=x;
ch[old][which]=ch[x][which^1], f[ch[old][which]]=old;
ch[x][which^1]=old,f[old]=x,f[x]=fold;
}
void splay(int x)
{
int u=x,v=0,fa;
sta[++v]=u;
while(!isrt(u)) sta[++v]=f[u],u=f[u];
while(v) pushdown(sta[v--]);
for(u=f[u];(fa=f[x])!=u;rotate(x))
if(f[fa]!=u)
rotate(get(fa)==get(x)?fa:x);
}
void Access(int x,int co)
{
int t=0,son;
while(x)
{
splay(x);
if(t) son=findrt(t), tr::update(1,n,1,st[son],ed[son],-1);
if(rson) son=findrt(rson),tr::update(1,n,1,st[son],ed[son],1);
col[x]=co,rson=t,t=x,x=f[x];
}
}
};
void dfs1(int u,int ff)
{
fa[u]=ff;
siz[u]=1;
dep[u]=dep[ff]+1;
ln[++tim]=u;
dfn[u]=st[u]=tim;
tr::update(1,n,1,dfn[u],dfn[u],dep[u]);
tree::f[u]=ff;
for(int i=hd[u];i;i=nex[i])
{
int v=to[i];
if(v==ff) continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[hson[u]]) hson[u]=v;
}
ed[u]=tim;
}
void dfs2(int u,int tp)
{
top[u]=tp;
if(hson[u]) dfs2(hson[u],tp);
for(int i=hd[u];i;i=nex[i])
{
int v=to[i];
if(v==hson[u]||v==fa[u]) continue;
dfs2(v,v);
}
}
int LCA(int x,int y)
{
while(top[x]^top[y]) dep[top[x]] < dep[top[y]] ? y = fa[top[y]] : x = fa[top[x]];
return dep[x] < dep[y] ? x : y;
}
int main()
{
// setIO("input");
scanf("%d%d",&n,&Q);
tr::maxv[0]=inf;
for(int i=1,u,v;i<n;++i)
{
scanf("%d%d",&u,&v);
addedge(u,v);
addedge(v,u);
}
dfs1(1,0);
dfs2(1,1);
int opt,x,y,lca,ou=0;
while(Q--)
{
scanf("%d",&opt);
switch(opt)
{
case 1 :
{
scanf("%d",&x);
tree::Access(x,++_curcol);
break;
}
case 2 :
{
scanf("%d%d",&x,&y);
lca=LCA(x,y);
ou=0;
ou+=tr::po(1,n,1,dfn[x]);
ou+=tr::po(1,n,1,dfn[y]);
ou-=tr::po(1,n,1,dfn[lca])<<1;
ou+=1;
printf("%d\n",ou);
break;
}
case 3 :
{
scanf("%d",&x);
printf("%d\n",tr::query(1,n,1,st[x],ed[x]));
break;
}
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号