BZOJ 2959: 长跑 LCT + 并查集 + 点双
Description
某校开展了同学们喜闻乐见的阳光长跑活动。为了能“为祖国健康工作五十年”,同学们纷纷离开寝室,离开教室,离开实验室,到操场参加3000米长跑运动。一时间操场上熙熙攘攘,摩肩接踵,盛况空前。
为了让同学们更好地监督自己,学校推行了刷卡机制。
学校中有n个地点,用1到n的整数表示,每个地点设有若干个刷卡机。
有以下三类事件:
1、修建了一条连接A地点和B地点的跑道。
2、A点的刷卡机台数变为了B。
3、进行了一次长跑。问一个同学从A出发,最后到达B最多可以刷卡多少次。具体的要求如下:
当同学到达一个地点时,他可以在这里的每一台刷卡机上都刷卡。但每台刷卡机只能刷卡一次,即使多次到达同一地点也不能多次刷卡。
为了安全起见,每条跑道都需要设定一个方向,这条跑道只能按照这个方向单向通行。最多的刷卡次数即为在任意设定跑道方向,按照任意路径从A地点到B地点能刷卡的最多次数。
Input
输入的第一行包含两个正整数n,m,表示地点的个数和操作的个数。
第二行包含n个非负整数,其中第i个数为第个地点最开始刷卡机的台数。
接下来有m行,每行包含三个非负整数P,A,B,P为事件类型,A,B为事件的两个参数。
最初所有地点之间都没有跑道。
每行相邻的两个数之间均用一个空格隔开。表示地点编号的数均在1到n之间,每个地点的刷卡机台数始终不超过10000,P=1,2,3。
Output
输出的行数等于第3类事件的个数,每行表示一个第3类事件。如果该情况下存在一种设定跑道方向的方案和路径的方案,可以到达,则输出最多可以刷卡的次数。如果A不能到达B,则输出-1。
题解:
考虑什么时候会产生点双: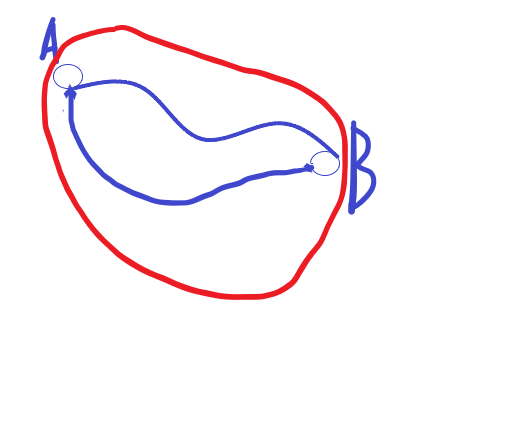
即 A,B 已联通,在 A,B 之间连一条边,则 A,B 与新边构成的环就是一个双联通分量(即一次可以全部到达的).
那么,我们就将这个环缩成一个点,把环中权值和赋值给环中一点.
当我们每次在进行各种操作时,要先在并查集中 find 一下祖先(一个点可能事先被缩进一个点双集合里了).
#include<bits/stdc++.h>
#define maxn 1000000
using namespace std;
void setIO(string a)
{
string in=a+".in",out=a+".out";
freopen(in.c_str(),"r",stdin);
}
struct Union
{
int p[maxn];
void init() { for(int i=0;i<maxn;++i) p[i]=i; }
int find(int x) { return p[x]==x?x:p[x]=find(p[x]); }
// 1 : disconnect
// 0 : connect
int merge(int x,int y)
{
int a=find(x),b=find(y);
if(a!=b) { p[a]=b; return 1; }
return 0;
}
}tree,con;
int n,Q;
int val[maxn],sumv[maxn];
#define lson ch[x][0]
#define rson ch[x][1]
#define get(x) (ch[f[x]][1]==x)
#define isRoot(x) (1^(ch[f[x]=tree.find(f[x])][1]==x||ch[f[x]=tree.find(f[x])][0]==x))
int ch[maxn][2],f[maxn],rev[maxn],sta[maxn],value[maxn];
void pushup(int x){ sumv[x]=sumv[lson]+sumv[rson]+val[x]; }
void mark(int x)
{
if(!x) return;
swap(lson,rson),rev[x]^=1;
}
void push(int x)
{
if(!x||!rev[x]) return;
mark(lson),mark(rson),rev[x]^=1;
}
void rotate(int x)
{
int old=f[x],fold=f[old],which=get(x);
if(!isRoot(old)) ch[fold][ch[fold][1]==old]=x;
ch[old][which]=ch[x][which^1],f[ch[old][which]]=old;
ch[x][which^1]=old,f[old]=x,f[x]=fold;
pushup(old),pushup(x);
}
void splay(int x)
{
x=tree.find(x);
int v=0,u=x,fa;
sta[++v]=u;
while(!isRoot(u)) sta[++v]=(f[u]=tree.find(f[u])), u=f[u];
while(v) push(sta[v--]);
for(u=tree.find(f[u]); (fa=f[x])!=u; rotate(x))
if(f[fa]!=u)
rotate(get(fa)==get(x)?fa:x);
}
void Access(int x)
{
int t=0;
x=tree.find(x);
while(x) splay(x),rson=t,pushup(x), t=x,x=(f[x]=tree.find(f[x]));
}
void MakeRoot(int x)
{
x=tree.find(x), Access(x), splay(x), mark(x);
}
void split(int x,int y)
{
x=tree.find(x),y=tree.find(y), MakeRoot(x), Access(y), splay(y);
}
void DFS(int x,int tp)
{
if(!x) return;
tree.p[x]=tp,DFS(lson,tp), DFS(rson,tp);
ch[tp][0]=ch[tp][1]=rev[tp]=0;
}
void link(int x,int y)
{
x=tree.find(x),y=tree.find(y), MakeRoot(x), f[x]=y;
}
int main()
{
// setIO("input");
tree.init(), con.init();
scanf("%d%d",&n,&Q);
for(int i=1;i<=n;++i) scanf("%d",&val[i]),value[i]=sumv[i]=val[i];
while(Q--)
{
int p,a,b,x,y;
scanf("%d%d%d",&p,&a,&b); // point a -> point b
switch(p)
{
case 1 :
{
a=tree.find(a), b=tree.find(b);
if(con.merge(a,b)) link(a,b);
else
{
// 不属于同一点双
if(a!=b)
{
split(a,b), val[b]=sumv[b], DFS(b,b);
}
}
break;
}
case 2 :
{
x=a, a=tree.find(a);
Access(a), splay(a), val[a]+=b-value[x],pushup(a),value[x]=b;
break;
}
case 3 :
{
a=tree.find(a),b=tree.find(b);
if(con.find(a)!=con.find(b)) printf("-1\n");
else
{
split(a,b), printf("%d\n",sumv[b]);
}
break;
}
}
}
return 0;
}


