最小堆

一、 满二叉树

一个深度为k，节点个数为2^k-1的二叉树为满二叉树，即一棵树深度为k，没有空位。

 

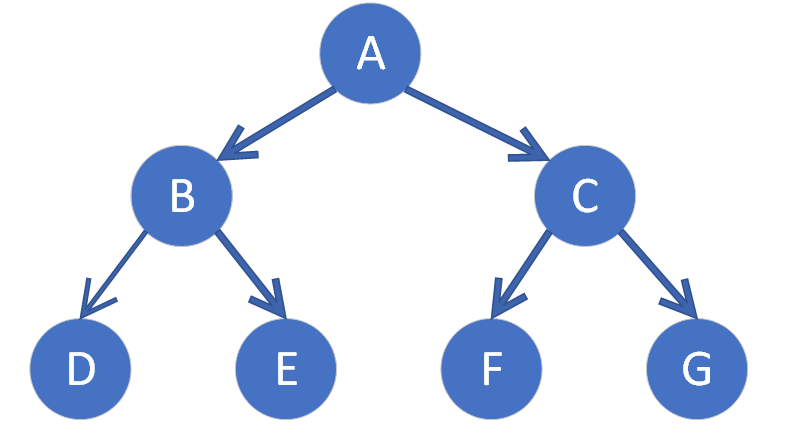
二、完全二叉树

一棵深度为k有n个节点的二叉树，对树中节点按从上至下、从左至右的顺序进行编号，如果编号为i(1<=i<=n)的节点与满二叉树中编号为i的节点的二叉树中位置相同，则这棵树为完全二叉树。满二叉树是特殊的完全二叉树。

 

三、完全二叉树与满二叉树性质

四、最小堆

最小堆是一种经过排序的完全二叉树，其中任意非终端节点数值均不大于其左子节点和右子节点的值。

如果一棵二叉树满足最小堆的要求，那么，堆顶（根节点）也就是整个序列的最小元素。如果从广度优先的方式从根节点开始遍历，可以构成序列。反过来，可以推演出序列构成二叉树的公式为：

•  对于序列下标为i（下标从0开始）的元素，左孩子的下标为left(i)=i*2+1，右孩子下标为right(i)=left(i)+1。

五、二叉树调整为最小堆的方法

1)      倒序遍历数列，因为下标在size/2之后的节点都是叶子结点，所以可以从size/2-1位置开始倒序遍历，减少比较次数。

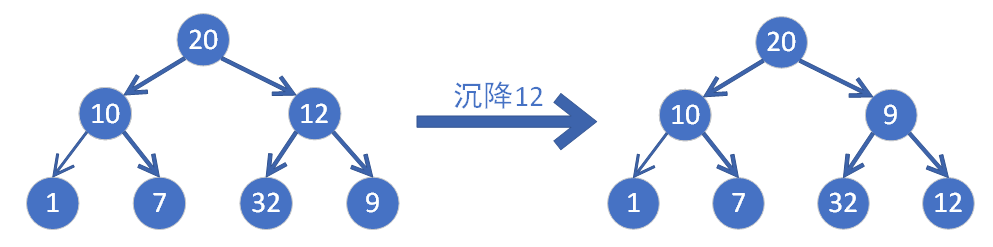
2)      对二叉树中的元素挨个进行沉降处理，沉降过程为：把遍历到的节点与左右子节点中的最小值比对，如果比最小值要大，那么和孩子节点交换数据，反之则不作处理，继续倒序遍历。

3)      沉降后的节点，再次沉降，直到叶子节点。

 

六、最小堆代码实现

package io.guangsoft;

public class MinPriorityQueue <T extends Comparable> {
    //存储堆中元素
    private T[] items;
    //记录堆中元素个数
    private int total;
    public MinPriorityQueue(int capacity) {
        items = (T[])new Comparable[capacity + 1];
        this.total = 0;
    }
    //获取队列中元素个数
    public int size() {
        return total;
    }
    //判断队列是否为空
    public boolean isEmpty() {
        return total == 0;
    }
    //判断堆中索引i处的元素是否小于索引j处的元素
    private boolean less(int i, int j) {
        return items[i].compareTo(items[j]) < 0;
    }
    //交换堆中i索引和j索引处的值
    private void swap(int i, int j) {
        T tmp = items[i];
        items[i] = items[j];
        items[j] = tmp;
    }
    //往堆中插入一个元素
    public void insert(T t) {
        items[++total] = t;
        swim(total);
    }
    //删除堆中最小元素，并返回这个最小元素
    public T delMin() {
        T min = items[1];
        swap(1, total);
        total--;
        sink(1);
        return min;
    }
    //使用上浮算法，使索引k处的元素能在堆中处于一个正确的位置
    private void swim(int k) {
        //通过循环比较当前节点和其父节点的大小
        while(k > 1) {
            if(less(k, k / 2)) {
                swap(k, k / 2);
            }
            k /= 2;
        }
    }
    //使用下沉算法，使索引k处的元素能在堆中处于一个正确的位置
    private void sink(int k) {
        //通过循环比较当前节点和其子节点中较小值
        while(2 * k <= total) {
            //找到子节点中的较小值
            int min;
            if(2 * k + 1 <= total) {
                if(less(2 * k, 2 * k + 1)) {
                    min = 2 * k;
                } else {
                    min = 2 * k + 1;
                }
            } else {
                min = 2 * k;
            }
            //判断当前节点和较小值的大小
            if(less(k, min)) {
                break;
            }
            swap(k, min);
            k = min;
        }
    }
    //主类
    public static void main(String args[]) {
        //创建最小优先队列
        MinPriorityQueue<Integer> queue = new MinPriorityQueue<>(8);
        //往队列中存数据
        queue.insert(1);
        queue.insert(6);
        queue.insert(2);
        queue.insert(5);
        queue.insert(7);
        queue.insert(3);
        queue.insert(8);
        queue.insert(4);
        //通过循环获取最小优先队列中的元素
        while(!queue.isEmpty()) {
            Integer min = queue.delMin();
            System.out.print(min + ",");
        }
    }
}

七、 PriorityQueue

　　PriorityQueue是一个基于优先级的无界队列，优先级队列的元素按照其自然顺序进行排序或者根据构造队列时提供的Comparator进行排序。其存储结构为数组，随着不断向优先级队列添加元素，其容量会自动扩容。

• heapify方法负责把序列转化为最小堆，即所谓的建堆。
• siftDown(k,x)方法用于沉降，根据comparator是否为null决定比较方法。沉降方法把不满足最小堆条件的父节点一路沉到最底部。siftDown的时间复杂度不会超出O(log₂n)。
• offer方法用于把数据入队，priorityQueue不允许存放null数据，与ArrayList留有扩容余量不同，当数组长度达到极限时才执行扩容。新添加的节点初始位置是在整个队列的末位，二叉树中，它一定是叶子节点，当它比父节点小时，需要进行上浮。
• grow(minCapacity)方法用于扩容，如果旧容量小于64，则扩容一倍+2，否则扩容1.5倍。扩容后校验容量，容量最大支持最大整型值。
• poll方法用来检索并移除此队列的头，最小堆虽然不能保证数列的顺序，但其堆顶元素始终是最小元素，而priorityQueue也只要求出队的对象优先级最高，当出队即堆顶元素移除后，其左孩子会变为堆顶，需要重新调整堆结构。而移除最小堆的任意叶子节点，最小堆性质不变。