BUAA_OO_2021-第一单元总结
一、总体
1.题目需求
读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用以及求和函数的表达式,输出恒等变形展开所有括号后的表达式。
2.题目分析
三次作业,题目要求层层递进,难度逐次加大,然总体思路不变,每个工程较上一个工程而言,皆是一次扩展与完善。一开始接触题目,没甚思路,于是去分析了预解析读入模式的输入,由此受到启发,决定仿效预解析的解析方式,先将原表达式做类似预解析的预处理,再进行化简计算,结合hint的提示,一个模糊的架构在头脑中成形。
由于前两个工程最终皆为第三个作业工程铺垫、服务,我们重点谈论第三次工程的设计与架构。
3.思路设计
3.1总体流程设计

3.2架构设计
结构层次

UML图
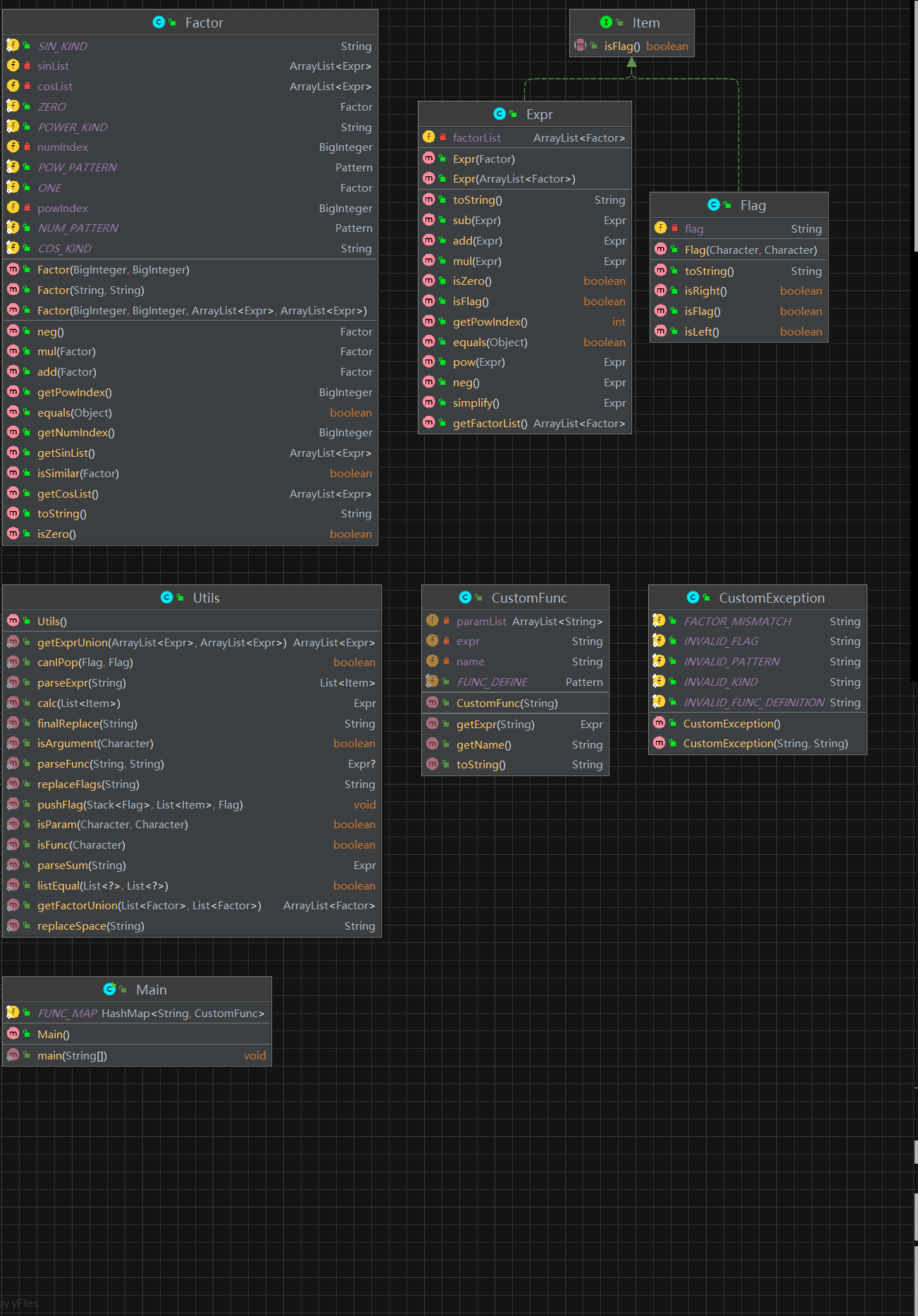
二、原子项
1.原子项组成:Factor
numIndex × powIndex × ΠsinList × ΠcosList
1.numIndex:数字系数(BigInteger)
2.powIndex:指数系数(BigInteger)
3.sinList:正弦函数项集合(ArrayList)
4.cosList:余弦函数项集合(ArrayList)
private BigInteger numIndex;
private BigInteger powIndex;
private ArrayList<Expr> sinList;
private ArrayList<Expr> cosList;
第二次作业中,三角函数的处理均采用HashMap对三角函数集合进行索引,使用字符串三角函数体中的内容作为字符串生成key,使用该项指数作为value,如此对运算的化简十分有益,省略掉了很多化简的步骤————因为在Calculate过程中绝大部分内容已经被化简。具体逻辑如下:
private TriMap sinMap;
private TriMap cosMap;
...
public String getKey() {
return String.format("coe:%s sin:%s cos:%s",
coeIndex.getKey(), sinMap.getValue(), cosMap.getValue());
}
然而考虑到第三次作业的递归嵌套,我绞尽脑汁也实在想不到好的key的生成方案,于是乎就只能选择ArrayList作为容器盛放三角函数项。
2.原子项运算
方法集合
| method | description |
|---|---|
| add() | 加法运算 |
| neg() | 取负运算 |
| mul() | 乘法运算 |
| isSimilar() | 判断是否同类项 |
| equals() | 判断是否全等项 |
| toString() | 转化为字符串输出 |
| isZero() | 判断是否为“0”项 |
查看方法具体内容
public Factor add(Factor otherFactor) throws CustomException {
if (!isSimilar(otherFactor)) {
throw new CustomException(CustomException.FACTOR_MISMATCH,otherFactor.toString());
}
return new Factor(numIndex.add(otherFactor.getNumIndex()),powIndex,sinList,cosList);
}
public Factor neg() {
return new Factor(numIndex.multiply(new BigInteger("-1")), powIndex, sinList, cosList);
}
public Factor mul(Factor otherFactor) {
BigInteger newPow = powIndex.add(otherFactor.getPowIndex());
BigInteger newNum = numIndex.multiply(otherFactor.getNumIndex());
ArrayList<Expr> newSinList = Utils.getExprUnion(sinList, otherFactor.getSinList());
ArrayList<Expr> newCosList = Utils.getExprUnion(cosList, otherFactor.getCosList());
return new Factor(newNum, newPow, newSinList, newCosList);
}
public boolean isSimilar(Factor otherFactor) {
if (otherFactor.getSinList().size() != sinList.size() ||
otherFactor.getCosList().size() != cosList.size()) {
return false;
}
if (!powIndex.equals(otherFactor.getPowIndex())) {
return false;
}
return Utils.listEqual(sinList,otherFactor.getSinList()) &&
Utils.listEqual(cosList,otherFactor.getCosList());
}
@Override
public boolean equals(Object obj) {
if (obj instanceof Factor) {
Factor otherFactor = (Factor) obj;
// 系数不等,值不可能相等
if (!otherFactor.getNumIndex().equals(numIndex)) {
return false;
}
// sin, cos 部分不相等,必然不会相等
if (otherFactor.getSinList().size() != sinList.size() ||
otherFactor.getCosList().size() != cosList.size()) {
return false;
}
// 若是系数不为0且指数也不相等,必然不会相等
if (!otherFactor.getNumIndex().equals(BigInteger.ZERO) &&
!otherFactor.getPowIndex().equals(powIndex)) {
return false;
}
return Utils.listEqual(sinList,otherFactor.getSinList()) &&
Utils.listEqual(cosList,otherFactor.getCosList());
} else {
return false;
}
}
@Override
public String toString() {
StringBuilder value = new StringBuilder();
if (numIndex.equals(BigInteger.ZERO)) {
return "0";
}
String flag = numIndex.compareTo(BigInteger.ZERO) > 0 ? "+" : "-";
value.append(flag);
boolean hasSuffix = false;
if (!numIndex.abs().equals(BigInteger.ONE)) {
hasSuffix = true;
value.append(numIndex.abs());
}
if (!powIndex.equals(BigInteger.ZERO)) {
if (hasSuffix) {
value.append(powIndex.equals(BigInteger.ONE) ?
"*x" : String.format("*x^%s", powIndex));
} else {
hasSuffix = true;
value.append(powIndex.equals(BigInteger.ONE) ?
"x" : String.format("x^%s", powIndex));
}
}
if (!sinList.isEmpty()) {
for (int i = 0; i < sinList.size(); i++) {
if (i == 0 && !hasSuffix) {
hasSuffix = true;
value.append(String.format("s((%s))", sinList.get(i)));
} else {
value.append(String.format("*s((%s))", sinList.get(i)));
}
}
}
if (!cosList.isEmpty()) {
for (int i = 0; i < cosList.size(); i++) {
if (i == 0 && !hasSuffix) {
hasSuffix = true;
value.append(String.format("c((%s))", cosList.get(i)));
} else {
value.append(String.format("*c((%s))", cosList.get(i)));
}
}
}
if (!hasSuffix) {
value.append("1");
}
return value.toString();
}
public boolean isZero() {
return numIndex.equals(BigInteger.ZERO);
}
三、表达式解析与运算
1.“预解析”
顾名思义,就是模仿官方包的预解析对目标表达式做转换为类似后缀表达式的处理。
1.1预替换
考虑到做类似字符自动机的逻辑,于是想到先将一些符号进行预替换。
幂符号 ‘**’ → ‘^’
正弦符号 ‘sin’ → ‘s’
余弦符号 ‘cos’ → ‘c’
求和符号 ‘sum’ → ‘#’
如此替换后,在对单个字符进行处理时,无需考虑后续符号内容即可判断出符号含义。
public static String replaceFlags(String tar) {
return tar.replaceAll("sin", "s").
replaceAll("cos", "c").
replaceAll("sum", "#").
replaceAll("\\*{2}", "^");
}
2.正式解析
2.1生成逆波兰式
前面已经提到,将模仿预解析官方包、结合逆波兰式转换的思路,对整个表达式进行解析。自动机逻辑如下:
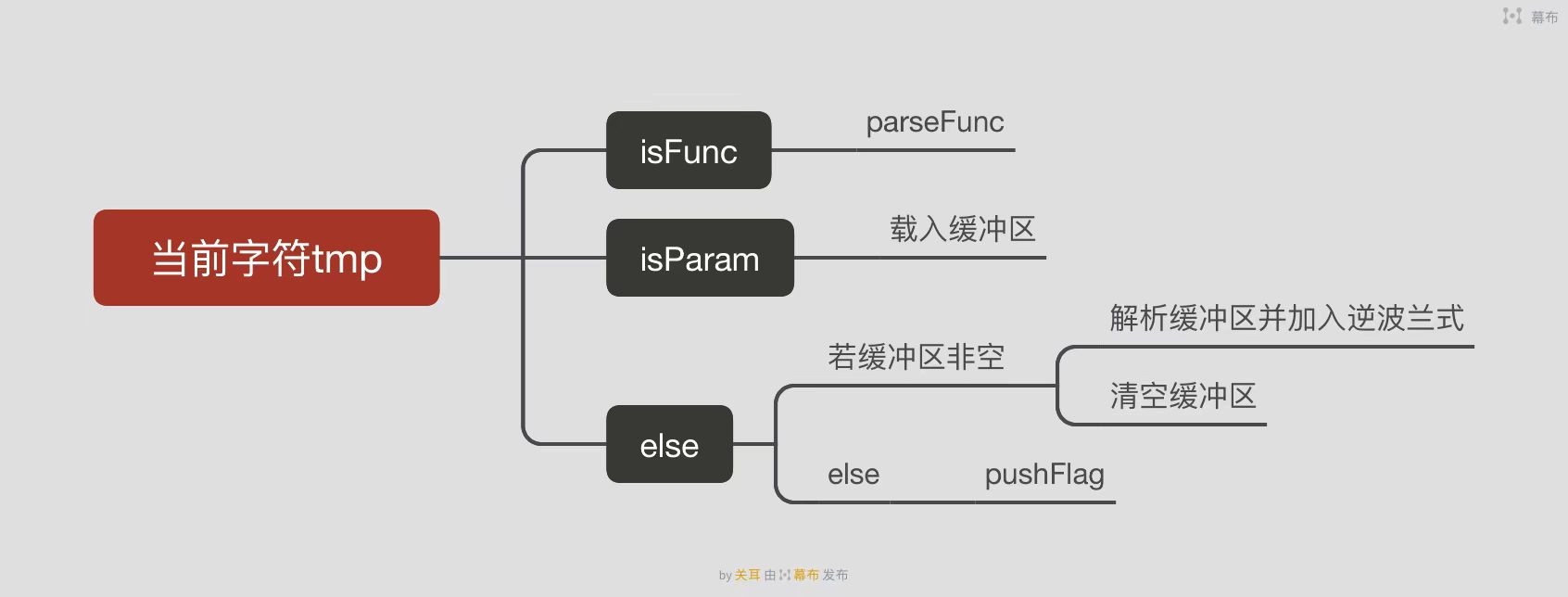
方法主体
public static List<Item> parseExpr(String str) {
String exprStr = replaceFlags(replaceSpace(str));
Stack<Flag> flagStack = new Stack<>();
List<Item> itemList = new ArrayList<>();
Character last = null;
StringBuilder buffer = new StringBuilder();
try {
for (int i = 0; i < exprStr.length(); i++) {
Character tmp = exprStr.charAt(i);
if (isFunc(tmp)) {
Stack<Character> bracketsStack = new Stack<>();
bracketsStack.push('(');
StringBuilder contentBuilder = new StringBuilder();
i += 2;
while (true) {
Character funcChar = exprStr.charAt(i);
if (funcChar.equals('(')) {
bracketsStack.push(funcChar);
} else if (funcChar.equals(')')) {
bracketsStack.pop();
}
if (bracketsStack.isEmpty()) {
break;
}
contentBuilder.append(funcChar);
i++;
}
String name = tmp.toString();
itemList.add(parseFunc(name, contentBuilder.toString()));
} else if (isParam(tmp, last)) {
buffer.append(tmp);
} else {
if (buffer.length() != 0) {
itemList.add(new Expr(new Factor(Factor.POWER_KIND, buffer.toString())));
buffer = new StringBuilder();
}
pushFlag(flagStack, itemList, new Flag(tmp, last));
}
last = tmp;
}
if (buffer.length() != 0) {
itemList.add(new Expr(new Factor(Factor.POWER_KIND, buffer.toString())));
}
while (!flagStack.isEmpty()) { // 清空符号栈
itemList.add(flagStack.pop());
}
} catch (CustomException e) {
e.printStackTrace();
}
return itemList;
}
关联方法
点击查看代码
public static boolean isFunc(Character character) {
return character == 's' || character == 'c' ||
character == '#' || character == 'f' ||
character == 'g' || character == 'h';
}
public static boolean isArgument(Character character) {
return character == 'x' || character == 'y' || character == 'z';
}
public static boolean isParam(Character tmp, Character last) {
return Character.isDigit(tmp) || isArgument(tmp) ||
(last != null && (last == '^' || last == '*') && (tmp == '+' || tmp == '-'));
}
public static Expr parseSum(String invocation) {
String[] params = invocation.split(",");
String iteratorName = params[0];
BigInteger begin = new BigInteger(params[1].trim());
BigInteger end = new BigInteger(params[2].trim());
String expr = params[3];
Expr ans = new Expr(Factor.ZERO);
for (;begin.compareTo(end) <= 0;begin = begin.add(BigInteger.ONE)) {
String str = expr.replaceAll(iteratorName,String.format("(%s)",begin));
ans = ans.add(Utils.calc(Utils.parseExpr(str)));
}
return ans;
}
public static Expr parseFunc(String name, String content) {
try {
if (name.equals(Factor.SIN_KIND) || name.equals(Factor.COS_KIND)) {
return new Expr(new Factor(name, content));
}
else if (Main.FUNC_MAP.containsKey(name)) {
return Main.FUNC_MAP.get(name).getExpr(content);
}
else if (name.equals("#")) {
return parseSum(content);
}
else {
return null;
}
} catch (CustomException e) {
e.printStackTrace();
return null;
}
}
public static boolean canIPop(Flag top, Flag now) {
if (top.toString().equals("pow")) {
return true;
} else if (top.toString().equals("mul")) {
return !now.toString().equals("pow");
} else if (top.toString().equals("neg") || top.toString().equals("pos")) {
return !(now.toString().equals("mul") || now.toString().equals("pow")
|| now.toString().equals("neg") || now.toString().equals("pos"));
} else {
return now.toString().equals("add") || now.toString().equals("sub");
}
}
public static void pushFlag(Stack<Flag> stack, List<Item> itemList, Flag flag) {
if (stack.isEmpty() || flag.isLeft()) {
stack.push(flag);
} else if (flag.isRight()) {
while (!stack.isEmpty() && !stack.peek().isLeft()) {
itemList.add(stack.pop());
}
// 弹出左括号
stack.pop();
} else {
while (!stack.isEmpty() && !stack.peek().isLeft() &&
canIPop(stack.peek(), flag)) {
itemList.add(stack.pop());
}
stack.push(flag);
}
}
2.2“计算”逆波兰式
计算逻辑较为简单,即采用基准思路,先不进行化简,而是暴力展开,具体方式如下:
其中:
pos:取正符号,直接忽略;
neg:取反符号;
add:加法;
sub:减法;
mul:乘法;
pow:幂运算。
点击查看代码
public static Expr calc(List<Item> parsedExprList) {
Stack<Expr> paramStack = new Stack<>();
for (int i = 0;i < parsedExprList.size();i++) {
Item tmp = parsedExprList.get(i);
if (tmp.isFlag()) {
Flag flag = (Flag) tmp;
if (!flag.toString().equals("pos")) {
Expr topParam = paramStack.pop();
if (flag.toString().equals("neg")) {
paramStack.push(topParam.neg());
continue;
}
Expr otherExpr = paramStack.pop();
if (flag.toString().equals("add")) {
paramStack.push(otherExpr.add(topParam));
}
else if (flag.toString().equals("sub")) {
paramStack.push(otherExpr.sub(topParam));
}
else if (flag.toString().equals("mul")) {
paramStack.push(otherExpr.mul(topParam));
}
else if (flag.toString().equals("pow")) {
paramStack.push(otherExpr.pow(topParam));
}
}
}
else {
paramStack.push((Expr) tmp);
}
}
return paramStack.pop();
}
四、表达式化简
表达式化简我在第三次作业中并未实现,在此仅简单谈谈预想。
1.化乘积为幂
对主表达式的每一个Factor,将Factor内部的乘积合并,并改写为幂的形式,对于三角函数,同样根据内部表达式的相同与否以及本身类型(是sin还是cos)决定是否合并相乘。
2.合并同类项
在对所有乘积进行合并和,我们已经默认每个Factor都是原子项的最简形式(即除了必要的‘’号外,无其他‘’号),于是便可根据isSimilar方法对主表达式的FactorList进行遍历,不断迭代,对于每个三角函数内的表达式采用递归方式化简。
五、评测机
1.整体设计
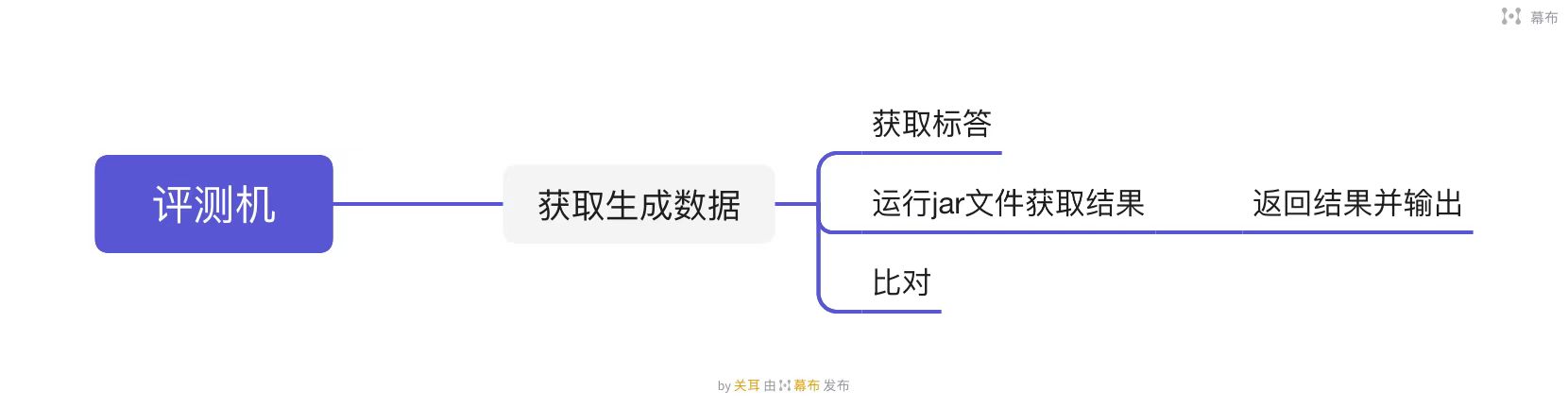
2.数据生成
对于随机数据生成思路,我所采用的思路与讨论区的思路大同小异。
由于simpy库的多重局限性,对于生成数据,将专门生成一份等价的python数据,用于使simpy库的化简函数快速得出结果.
3.评测比对
3.1处理java输出
java输出默认已经化简可处理;
def execute_java(self, std_java: str):
cmd = ['java', '-jar', self.setting_dic['tar_path']]
proc = subprocess.Popen(cmd, stdin=subprocess.PIPE, stdout=subprocess.PIPE, stderr=subprocess.STDOUT)
stdout, stderr = proc.communicate(std_java.encode())
return stdout.decode().split("\n")[1]
3.2获得python标答
根据python输入进行化简,获得标答
def get_stdout(self, data: turtle):
std_java, std_py = data
java_res = self.execute_java(std_java)
python_res = sympy.trigsimp(std_py)
return java_res, python_res
3.3答案校验
考虑到字符串直接比较的复杂性高以及容错性低,于是采用java输出与python标答作差的思路,若最终结果等价于0,则说明答案无误。
def run(self):
data = answer.get_data()
std_java, std_py = data
res = self.get_stdout(data=data)
java_res, py_res = res
difference = sympy.simplify(sympy.trigsimp(str(java_res).strip() + "-(" + std_py + ")"))
judge_res = 'Wrong answer. We got difference %s' % str(difference) if difference != 0 else 'Accepted'
return {'std_in': std_java, 'py_res': py_res, 'java_res': java_res, 'difference': difference,
'judge_res': judge_res}
4.性能提升
4.1 失败的尝试
考虑到jar包执行的时间,首先我默认为(误以为)这段时间可以视作IO等待时间处理,于是想都没想直接决定采用协程优化。
async def auto_run(self):
task_get_data = asyncio.create_task(answer.get_data())
data = await task_get_data
res = asyncio.create_task(self.run(data=data))
await res
return res.result()
async def work(self):
global begin
task_list = [asyncio.create_task(self.auto_run()) for _ in range(self.setting_dic['num'])]
await asyncio.wait(task_list, timeout=None)
for task in task_list:
print(task.result())
print("begin:", begin)
print("end:", str(datetime.datetime.now()))
最终效率与普通单线程评测机对比时,结果是让人失望的(以100组数据为例):
协程优化评测机效率:
100组数据跑了接近1分钟时间
普通评测机效率:

虽然也是将近一分钟,但是明显更快;
结论:尽管有偶然性、数据相异的原因在其中,但有一点却是毋庸置疑————那就是优化了个寂寞。
4.2改进与提高

经过观察计算机性能监控,发现CPU一直处在高负荷状态,即说明运行jar以及评测的其他过程中并无太多IO等待时间,————评测机属于CPU密集型任务,显然多线程和协程优化均不合适,采用多进程才是最佳的优化途径:
if __name__ == '__main__':
start = datetime.datetime.now()
pool = Pool(processes=4)
test = TestMachine.auto("F:/OO/tasks/homework3/out/artifacts/homework3_jar/homework3.jar", 50)
res_list = []
for i in range(test.setting_dic['num']):
res = pool.apply_async(test.run)
res_list.append(res)
pool.close()
pool.join()
for response in res_list:
print(response.get())
end = datetime.datetime.now()
再次进行测试,结果如下:

显然速度明显提升,大约为4倍于普通评测机的速度。
六.反思与总结
1.反思
1.1第一次作业分析

本次BUG出在Factor类的toString方法上,导致系数为1的项输出出现错误。
类复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Factor | 1.90 | 6 | 19 |
| Flag | 3.25 | 10 | 13 |
| Expression | 3.13 | 10 | 47 |
| Total | 79 | ||
| Average | 2.72 | 8.67 | 26.33 |
| 方法复杂度分析 | |||
 |
可以看出,各类耦合度较低,各方法复杂度较低,整体设计耦合度适中,架构较为清晰。
1.2第二次作业分析

本次作业的bug仍然出在细节之上:未考虑函数名(f,g,h等)后面的空格,导致一旦数据出现函数名后空格,则解析自定义函数出现异常,从而出现错误。
类复杂度分析
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| Base | 2.46 | 15 | 32 |
| CustomFunc | 3.00 | 7 | 12 |
| Expr | 2.08 | 4 | 25 |
| Factor | 1.75 | 6 | 21 |
| Flag | 2.86 | 10 | 20 |
| Main | 3.33 | 13 | 40 |
| Sum | 1.67 | 2 | 5 |
| TriMap | 3.00 | 6 | 21 |
| Total | 176 | ||
| Average | 2.51 | 7.88 | 22.00 |
方法复杂度分析

可见Base类以及主类Main类复杂度偏高,根据方法复杂度分析可见,Main类中preParse()以及simplify()方法耦合度较高,圈复杂度高,模块设计复杂度越高,耦合性越大。
1.3 第三次作业分析(未被测出)
类复杂度分析
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| CustomException | 1.00 | 1 | 2 |
| CustomFunc | 3.00 | 8 | 12 |
| Expr | 2.00 | 6 | 28 |
| Factor | 3.00 | 15 | 42 |
| Flag | 2.80 | 10 | 14 |
| Main | 2.00 | 2 | 2 |
| Utils | 2.93 | 11 | 44 |
| Total | 144 | ||
| Average | 2.62 | 7.57 | 20.57 |
方法复杂度分析
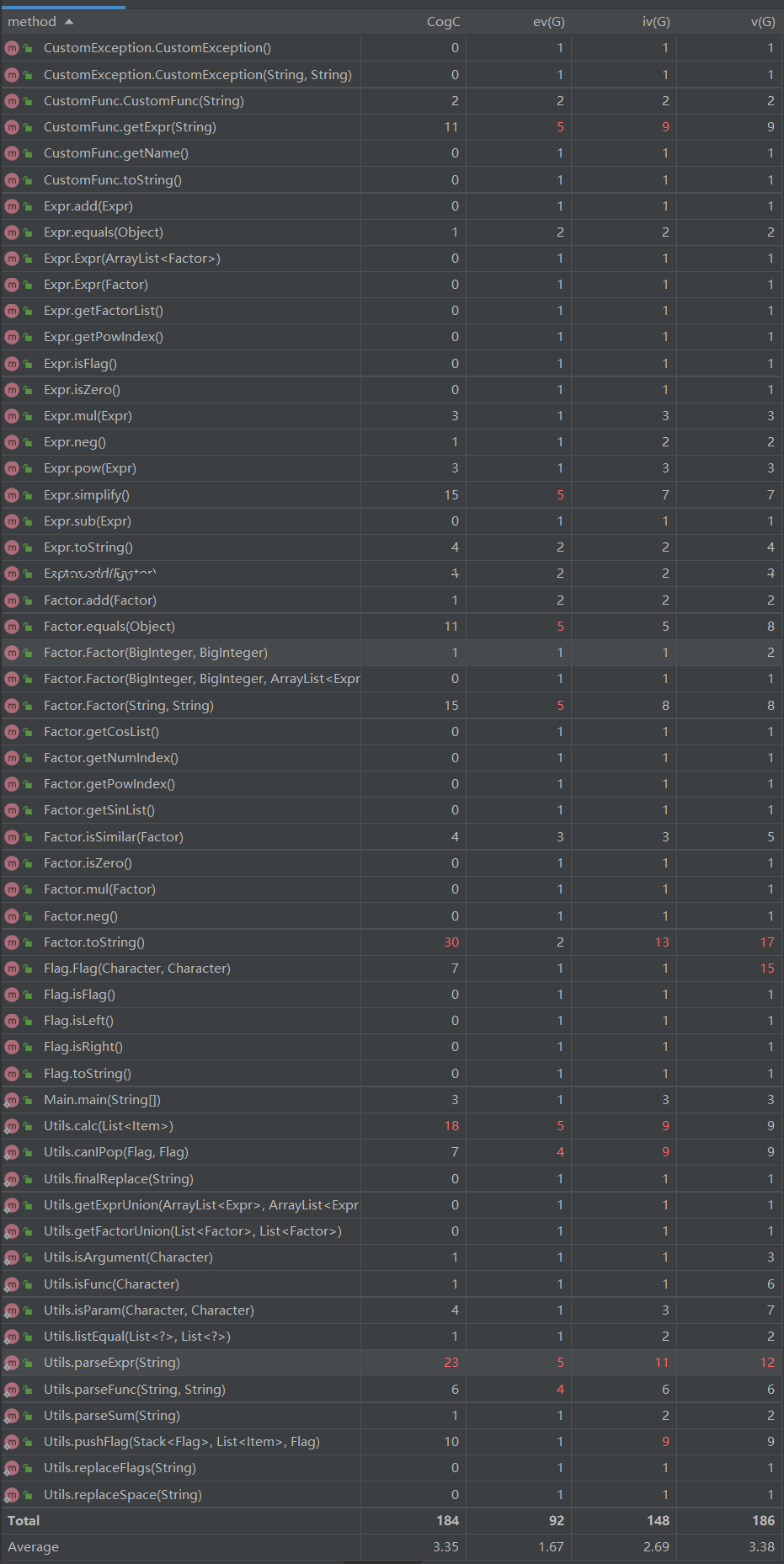
本次仍可以发现,Factor类与Utils类复杂度过高,设计思路仍然考虑不周,需要继续完善。
本次作业问题出在三角函数内表达式的括号处理问题,未能在函数字符串替换时对括号内表达式整体加上括号,从而导致解析表达式时出现错误。
2.个人感受
经历了OO第一单元的三次作业和三次课上实验,着实体会了复杂工程的架构的难处、妙处,比之有着“六系魔鬼”之称的计组,我看也不遑多让。
这不是我第一次接触面向对象工程,确是第一次采用系统的面向对象思想对整个工程的架构进行设计、架构,采用严格的代码风格约束,同时使用git版本控制工具进行提交、修改工程。
OO所有作业均采用Java语言进行编程,Java语言也确实是学习面向对象思维的不二选择(虽然我个人对Java没啥好感,感觉过于笨重),通过本单元的学习,我对Java语言的理解更加通透,对“Java编程思想”也有了更进一步的认识,同时还复习了正则表达式的使用。由于本单元多着力于对字符串解析的考查,经过本单元的训练,我对字符串的解析也有了更深层次的理解。通过对表达式结构进行建模,完成单变量多项式的括号展开,初步体会到了层次化设计的思想。



