多边形三角剖分问题综述

​ 内容包括：剖分算法、评价标准。

关键词：voronoi、Delaunay

一、问题描述

多边形是由一系列首尾相接的直线段组成的。凸多边形边界上或内部的任意两点所连成的直线段上所有的点均在该凸多边形的内部或边界上。与凸多边形对应的就是凹多边形。简单多边形三角剖分问题的定义是:将简单多边形P分解为一系列不相重叠的三角形,同时不产生新的顶点,其结果记为T(P)。

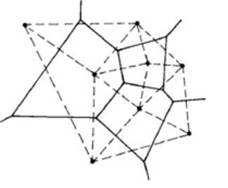谈到三角剖分，经典Delaunay三角剖分，Delaunay三角剖分与Voronoi图互为偶图，一一对应，简单了解一下Voronoi图。Voronoi图其实就是由每个节点到相邻节点的垂直平分线组成的多边形构成的一个多边形集合，下图一个8节点的Voronoi图，其中的实线部分正是各个多边形。

一般情况下，Voronoi图的一个顶点同时属于三个Voronoi多边形，每个Voronoi多边形内有且仅有一个节点。连接三个共点的Voronoi多边形分别对应的三个节点则形成一个Delaunay三角形，所有这样的三角形的集合就是著名的Delaunay三角剖分。上图中的虚线部分就是与该Voronoi图对偶的Delaunay三角剖分。

Delaunay三角剖分概述

简单多边形P的Delaunay三角剖分(简记为DT(P))是所有内边都是局部优化的T(P),它具有最小内角最大以及平均形态比最大的性质，能够尽可能地避兔病态三角形的出现，更适合于有限元网格自动生成。如果存在一个简单多边形的三角剖分T(P),则对三角剖分中不是优化的边进行对角线交换,可以在有限次的局部优化操作后转化为DT(P)。

二、算法描述

关于Delaunay剖分三角形的算法，有翻边算法、逐点插入算法、分割合并算法、Bowyer-Watson算法等。这几种算法中，逐点插入算法比较简单、易懂，下面仅仅针对该算法进行讨论，该算法也是目前使用最为广泛的Delaunay算法。

逐点插入的Lawson算法基本原理为：首先建立一个大的三角形或多边形，把所有数据点包围起来，向其中插入一点，该点与包含它的三角形三个顶点相连，形成三个新的三角形，然后逐个对它们进行空外接圆检测，同时用Lawson设计的局部优化过程LOP进行优化，即通过交换对角线的方法来保证所形成的三角网为Delaunay三角网。

三、评分标准

上述基于散点的构网算法理论严密、唯一性好，网格满足空圆特性，较为理想。由其逐点插入的构网过程可知，遇到非Delaunay边时，通过删除调整，可以构造形成新的Delaunay边。在完成构网后，增加新点时，无需对所有的点进行重新构网，只需对新点的影响三角形范围进行局部联网，且局部联网的方法简单易行。同样，点的删除、移动也可快速动态地进行。但在实际应用当中，这种构网算法当点集较大时构网速度也较慢，如果点集范围是非凸区域或者存在内环，则会产生非法三角形。感觉和多边形划分稍微有些差距，但是本质差不多，注意lop进行优化，得到比较好的结果。