吴恩达机器学习（2）多变量线性回归

在我们的实际生活中遇到的问题一般都有多个变量影响，就拿上个例子房价来说，影响房价的因素还有地段、朝向、面积大小等等，所以必须采用多变量，这样拟合的模型才更准确。

• 模型：

这里考虑了四个因素对房价的影响，如下图所示：变量类型分为x1、x2、x3、x4，其中n表示特征的数量m表示样本数。

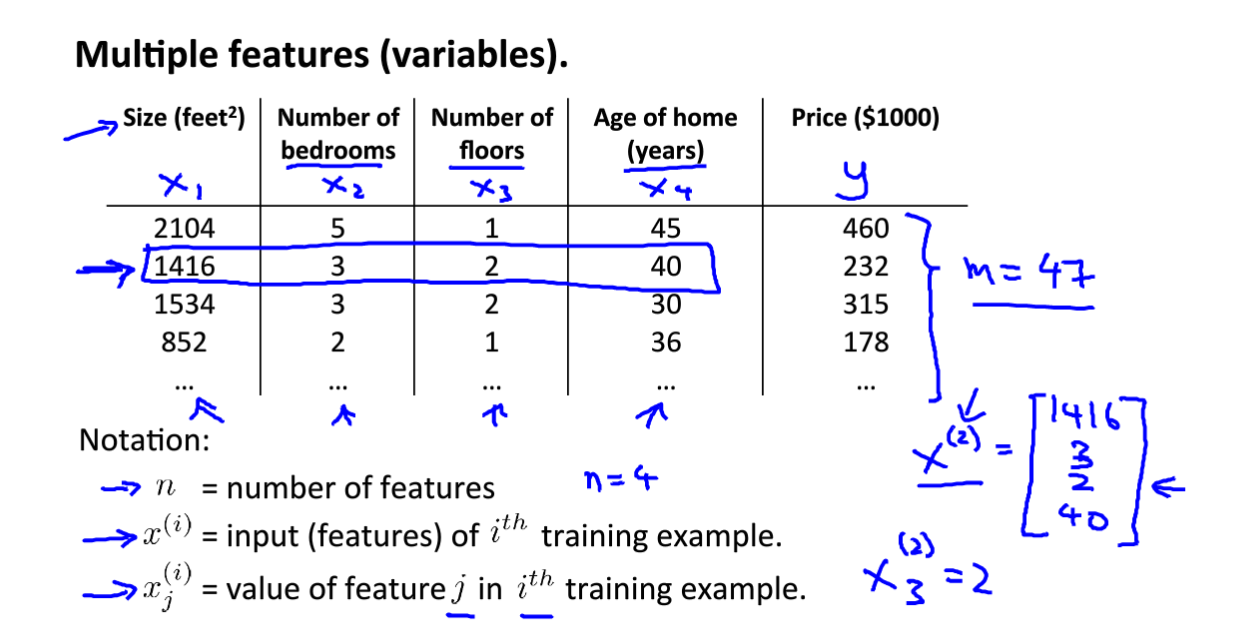
根据上面的多变量模型建立假设函数：如下图所示，我们把x0设为1，另外写成X列向量和θ列向量，最后整个假设模型函数写成θ的转置与X向量的乘积。

• 梯度下降：

在多变量线性回归中，我们的梯度下降与单变量的梯度下降是差不多的，还是预设定参数减去学习率与原参数在代价函数上偏导数的乘积，直到下降到最优解。

下图左图是单变量线性回归的梯度下降计算，右图是多变量的梯度计算。

• 特征缩放：

虽然多元线性回归的梯度下降方法和单变量回归没有太大的差别，但是多元线性回归涉及到单变量回归没有的问题，就是多个特征值的取值差别过大，导致模型很难拟合。这里我们需要运用特征缩放的方法对数据进行预处理。

特征缩放其实很简单，比如我们的两个变量房屋的面积和房间数。房屋的面积 的范围在0-2000英寸，

而我们的房间数在1-5间，这两个特征值就相差过大，导致梯度下降的困难。这里我们只需要把我们的房屋面积除以2000，房间数除以5，这样我们两个特征值的范围就在0-1之间，梯度下降就更加容易。

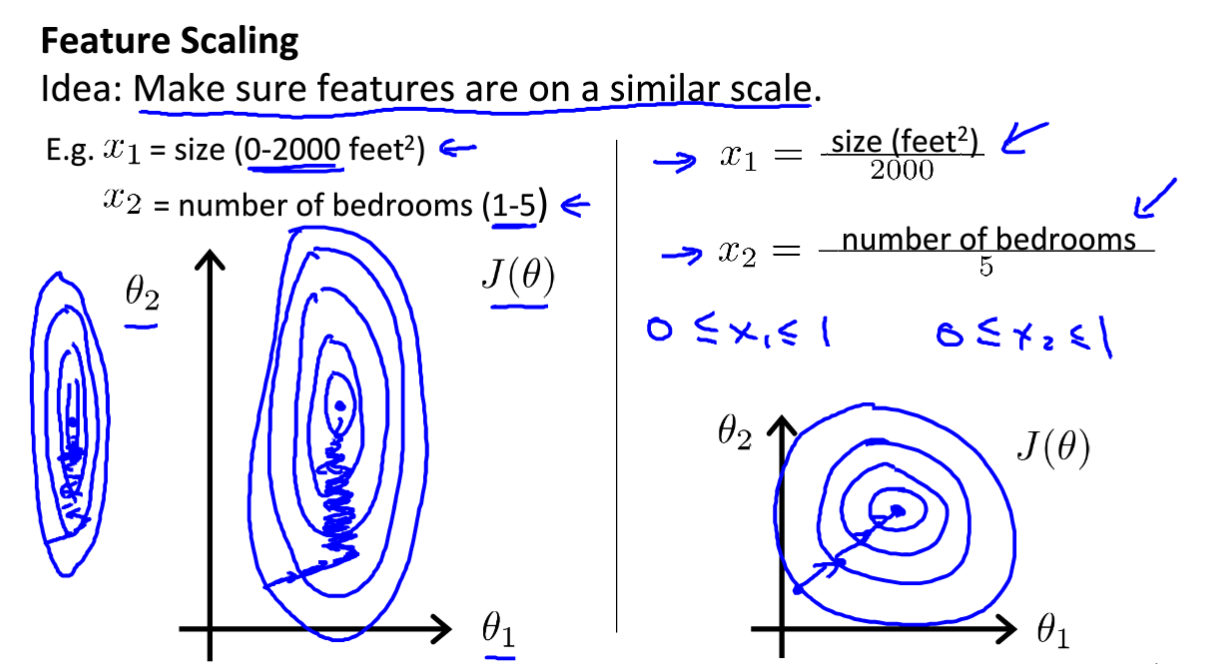
• 学习率的选择：

我们可以绘制迭代次数与代价函数的值的关系图来判断学习率的选择。

如果随着迭代次数的增加代价函数的输出值升高，则判断当前的学习率较小，需要增大学习率；如果输出的代价函数值随着迭代次数忽高忽低，则判断学习率太大需要减小。总的来说就是学习率太小，梯度下降的太慢；学习率太大，可能会无法找到最优点。

另外，我们推荐学习率的改变方式是每十倍取值，比如0.001偏小了我们下次就取0.01，再偏小再取0.1。

 

 

•  特征与多项式回归：

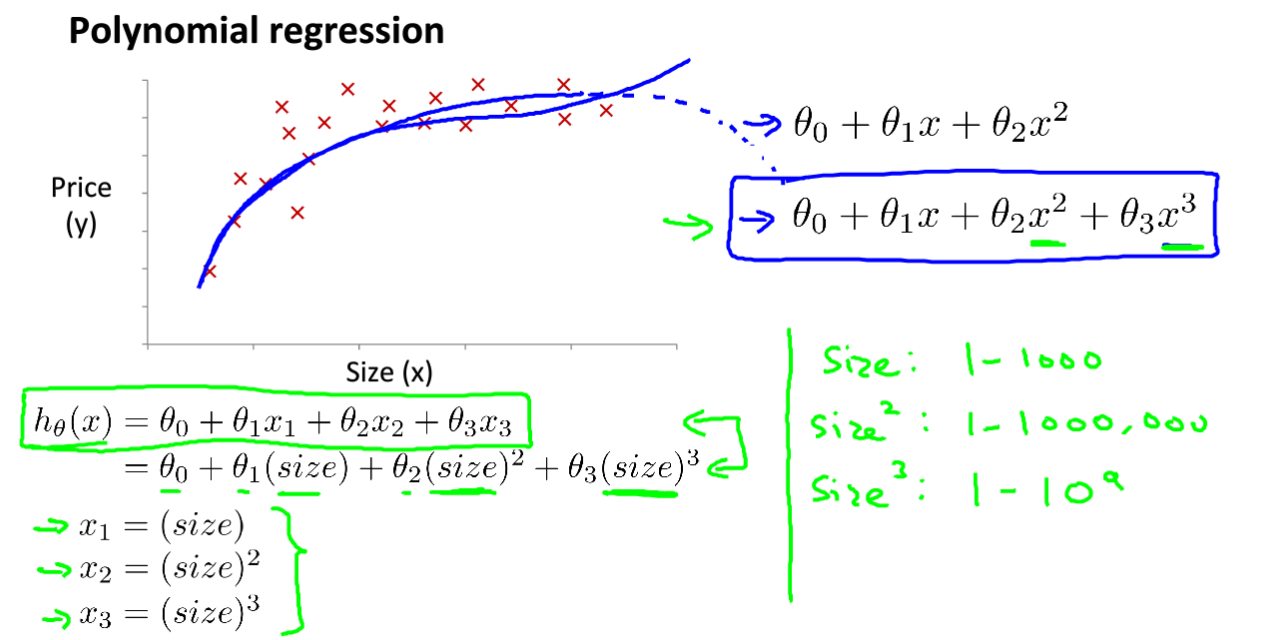
很多时候，我们所拥有的数据集分布可能不是直线的，可能是曲线的，那么就可以采用非直线型函数。比如房价问题，可能是二次函数，也可能是三次函数。

对于下面的房价模型，采用三次拟合函数模型，然后进行每项替换，就变成了x1、x2、x3的线性拟合问题，另外需要特征缩放，毕竟三次与1次的差距很大。

 

正规方程：

我们的梯度下降法是在代价函数取得最小的时候，求解到的值。那么为什么不能直接对代价函数求解相应变量的偏导数，再等于0，求解此时的参数。这里就给出了正规方程的求解方式，直接求导等于0.

但在这里，参数少还好说，但是如果参数很多的话就得求解很多次，很麻烦。所以需要用矩阵的形式来给出算式。如右图所示。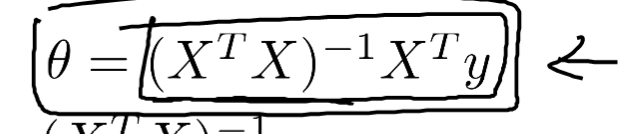我们的解也是一个矩阵。

 

上面给出的正规方程解法，一步我们就可以得到我们想要的结果，是不是很方便，但是正规方程真的这么万能的话我们也不会在前面废这么大的劲来讲解梯度下降法。这里我们就给出两种方法的优劣。
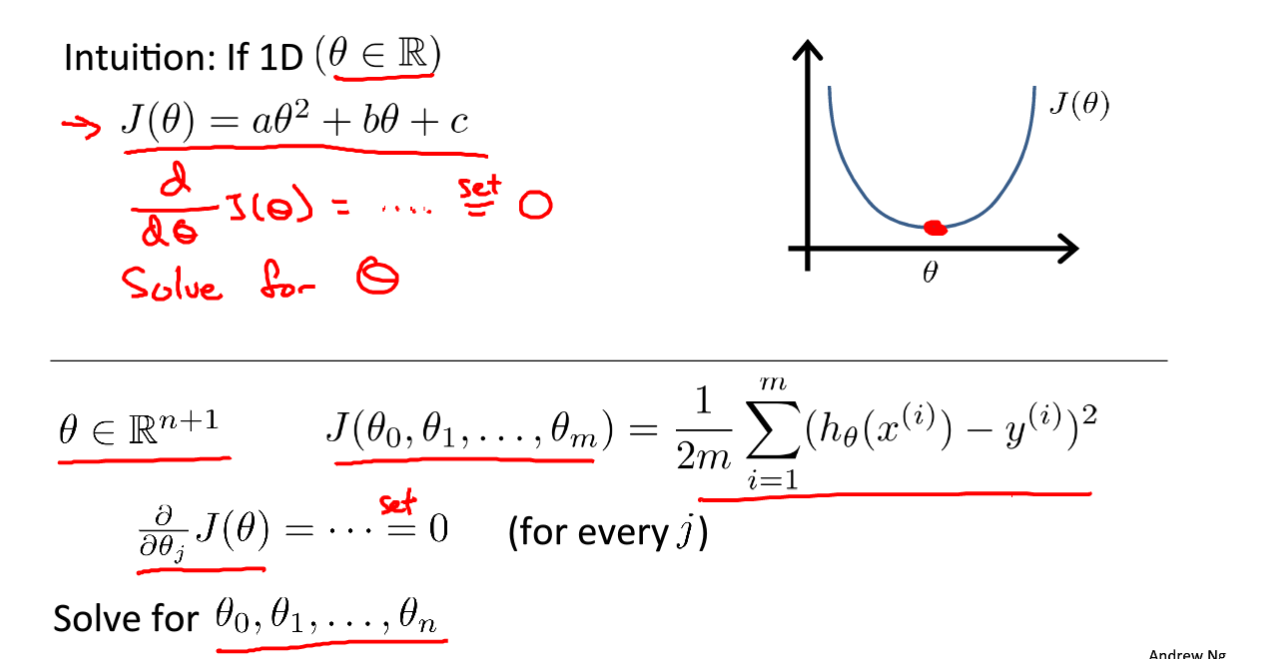
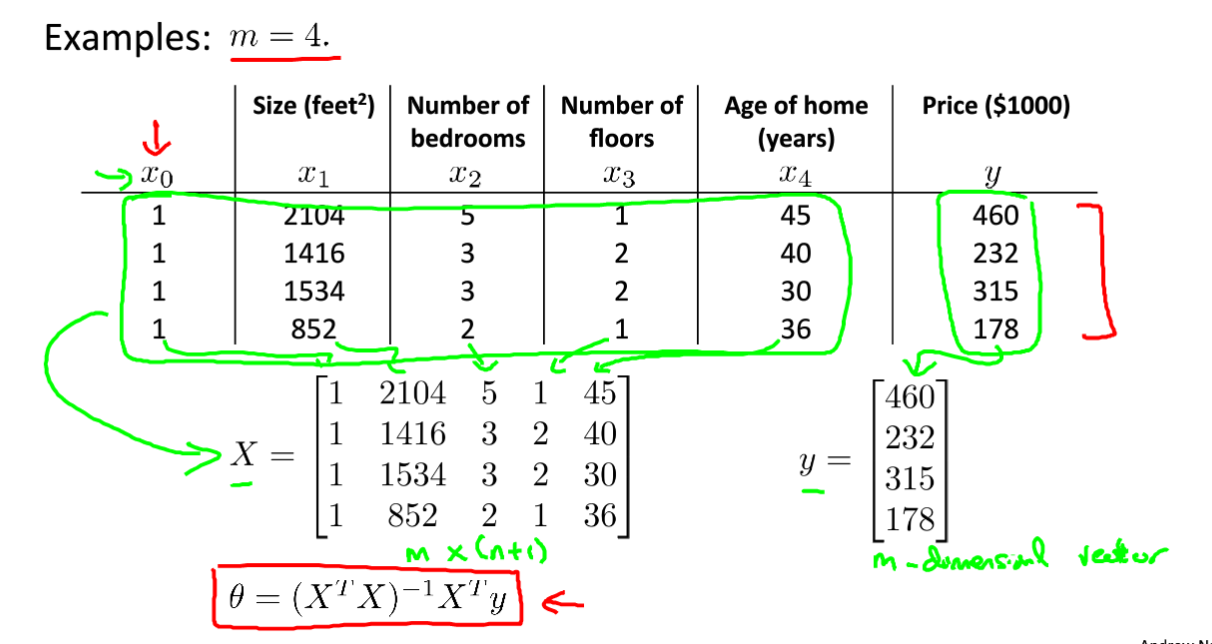
首先梯度下降我们要确定学习率，而且需要很多次迭代来训练，费时费力，正规方程则不需要。
但是我们特征过多的话，正规方程求解的时间维度是O（n ^ 3），这就需要比梯度下降更多的时间来求解。梯度下降适用于更多的情况，而且符合机器学习的方法，所以我们在做机器学习更倾向于用梯度下降而不是用正规方程。