概率论
网上找了一个概率总结PPT,放到这里可以借鉴,没有必要以后再去到处搜了,当然要想真正学好得看更加详细的资料。
自然界发生的现象分为两类。一类现象在一定条件下发生的结果是完全可以预知的,称为必然现象。另一类现象发生的结果事先是无法准确预知的,称为偶然现象或随机现象。随机现象中的事件可能发生也可能不发生。一个随机事件A发生的可能性的大小,用一个介于0~1的数表示出来。
随机现象中,变量的取值是不确定的,称为随机变量。描述随机变量取值概率的函数称为概率分布。对于随机变量,通常主要关心它的两个数字特征:数学期望(或称均值)——用于描述随机变量的平均值,方差——用于描述随机变量分布的差异程度,方差的算术平方根称为均方差(或标准方差)。另外协方差和相关系数用于描述两个随机变量的线性关联程度。
随机变量的分布,根据其取值特点不同主要分为离散型和连续型两类,若用变量ξ 表示实验仪“正面向上次数”,其取值可能为0,1,2,…,10(离散点集),则为离散型随机变量。典型的离散分布有离散均匀分布、二项分布、Possion分布等。典型的连续型分布有均匀分布、正态分布、指数分布、χ²分布、t分布和F分布等。
| 序号 | 中文函数名 | 英文函数名 | 英文简写 | 备注 |
|---|---|---|---|---|
| 1 | Beta分布 | Beta | beta | |
| 2 | 二项分布 | Binomial | bino | |
| 3 | 卡方分布 | Chisquare | chi2 | 抽样 |
| 4 | 指数分布 | Exponential | exp | |
| 5 | F分布 | F | f | 抽样 |
| 6 | Gamma分布 | Gamma | gam | |
| 7 | 几何分布 | Geometric | geo | |
| 8 | 超几何分布 | Hypergeometric | hyge | |
| 9 | 对数正态分布 | Lognormal | logn | |
| 10 | 负二项分布 | Negative Binomial | bbin | |
| 11 | 非中心F分布 | Noncentral F | ncf | |
| 12 | 非中心t烦恼 | Noncentral t | nct | |
| 13 | 非中心卡方分布 | Noncentral Chi-square | ncx2 | |
| 14 | 正态分布 | Normal | norm | |
| 15 | 泊松分布 | Poisson | poiss | |
| 16 | 瑞利分布 | Rayleigh | ray1 | |
| 17 | T分布 | T | t | 抽样 |
| 18 | 均匀分布 | Uniform | unif | |
| 19 | 离散均匀分布 | Discrete Uniform | unid | |
| 20 | Weibull分布 | Weibull | weib |
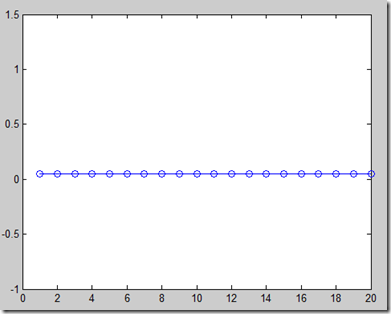
1、离散均匀分布
设一个随机变量ξ服从离散均匀分布,如果它的概率分布为
图1 离散均匀分布
即ξ 以相同的概率取{1,2,…,n}中的值。
>> n=20;
>> x=1:n;
>> y=unidpdf(x,n);
>> plot(x,y,'o-');
2、二项分布B(n,p)
若将实验可能结果分为两个:A发生或A不发生,则称此随机实验为Bernoulli实验。
设随机变量
那么,ξ 服从一个简单离散型分布P(ξ=0)=1-p,称为Bernoulli分布或0-1分布。
将Bernoulli实验独立重复进行n次,称为n重Bernoulli实验,n重Bernoulli实验中A发生的次数的分布为
称为参数为n,p的二项分布,记为ξ~B(n,p)。二项分布的数学期望E(ξ)=np,
方差D(ξ)=np(1-p)。
>> x=0:50;
>> y=binopdf(x,500,0.05);
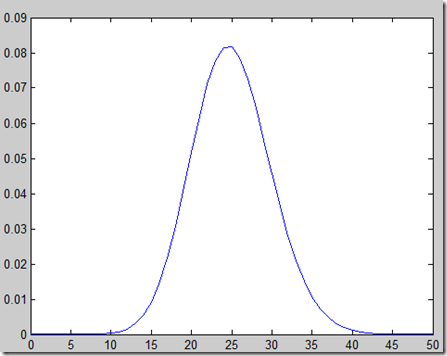
>> plot(x,y);
图2 二项分布
3、均匀分布
先看图吧:
>> x=-10:0.1:10;r=1;
>> y=unifpdf(x,0,2*pi*r);
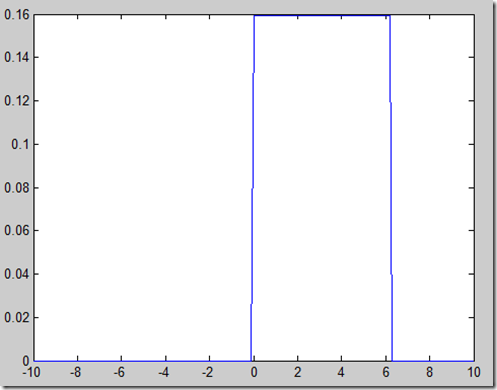
>> plot(x,y);
图3 均匀分布
均匀分布(图3)是一个简单而重要的连续型概率分布,其密度函数为
它的实际意义是:随机变量取值总是在(a,b)内,并且每一点附近取值可能性相同.均匀分布的数学期望E(ξ)=(a+b)/2,方差D(ξ)=(b-a)²/12。特别地,区间(0,1)上的均匀分布称为标准均匀分布。
4、正态分布N(μ,σ²)
正态分布是应用最广泛的一类概率分布,其概率密度函数为
记为N(μ,σ²),其中μ是随机变量取值的平均,而σ表征了随机变量取值的差异。特别地,N(0,1)称为标准正态分布。最典型的正态分布的例子是测量误差,很多事件都服从正态分布。正态分布的数学期望E(ξ)=μ,方差D(ξ)=σ²。
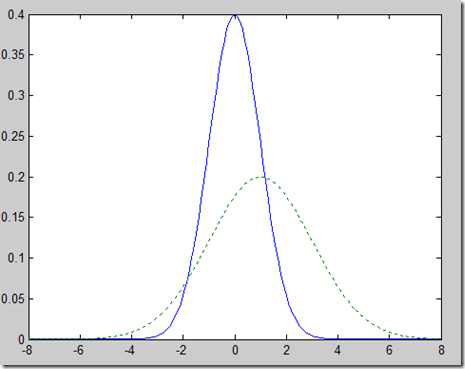
正态分布有很多的性质。设,i=1,2,…,n,且这些随机变量相互独立,那么它的线性函数任然是正态分布。特别地,若ξ~N(μ,σ²),那么(ξ-μ)/σ~N(0,1),即任何正态分布可以通过线性变换转化为标准正态分布(图4)。
>> x=-8:0.1:8;
>> y=normpdf(x,0,1);
>> y1=normpdf(x,1,2);
>> plot(x,y,x,y1,':');
图4 标准正态和飞标准正态
5、分布函数和逆分布函数
设ξ 是一个随机变量,称
F(x)=p(ξ≤x), -∞<x<∞
为ξ 的分布函数,它是ξ 不超过x的概率分布的累加,所以也称为累计概率函数。分布函数的逆函数称为逆分布函数,它构成映射p->xp,使得
p(ξ≤xp)=p, 0≤p≤1
xp也称为100p%下分位数。
6、统计量
所谓总体就是一大批具有特定意义的待分析的随机数据,数学上用一个未知的概率分布表示。在多数情况下,总体的分布类型是已知的,只是某些参数未知。例如,已知总体服从正态分布N(μ,σ²),但其中参数μ,σ²未知。总体的一部分数据x1,x2,…,xn称为一个容量为n的样本。数理统计就是要根据样本对总体进行推断。
不含未知参数的样本的函数称为统计量,他是样本特征的集中反映,选取一个正确的统计量是Tatyor推断的关键,几个最基本的统计量如下。
(1)样本均值,反映了样本取值的平均值。
(2) 样本方差 ,样本标准差s=sqrt(s^2),反映了样本对于均值的偏离程度。样本极差x(n)-x(1)也是离散程度的反映。
(3) 样本协方差 ,样本相关系数
,其中sx,sy为样本标准差。相关系数反映了样本x1,x2,…xn与样本y1,y2,…,yn的线性相关关系。若r接近于1,x较大时y也较大;若r接近于-1,说明x较大时y较小;若r接近于0,说明x与y取值大小无线性相关关系,总之,|r|接近1说明线性关系密切。
(4) 样本百分位数,将x1,x2,…,xn从小到大顺序排为x(1),x(2),…,x(n),q%上分位数(等价于(100-q)%下分位数)表示这样一个值xq:比xq大的样本占样本总数的q%。50%上分位数(等价与50%下分位数)称为中位数,比它大的样本与比它小的样本一样多。
7、参数估计
在统计推断中,总体参数θ未知,需要根据样本x1,x2,…,xn估计θ的值。参数估计分为两类:点估计和区间估计。点估计就是直接给出θ的估计值,如“θ大约等于1.3”。但点估计缺乏对精度的说明。而区间估计给出θ的估计值区间,并附加一个概率,如“θ的95%置信区间是[1.26,1.36]”,含义是:θ在[1.24,1.36]内的概率为0.95。
设有总体F(x,θ),其中参数θ未知,现有来自F(x,θ)的一个样本x1,x2,…,xn,要估计θ的值。如有区间CI=[θ1,θ2],使得
P(θ1<θ<θ2)=1-α
称CI为θ的100(1-α)%置信区间。
设ξ 为正态总体N(μ,σ²),μ,σ未知,x1,x,2,…,xn为样本,那么μ和σ的点估计分别为
μ=x拔,σ=s
它们的100(1-α)%置信区间分别为
式中:表示自由度为(n-1)的t分布的100(1-α/2)%下分位数。
8、假设检验
许多统计推断常涉及对某假设的正确性作出“是”与“否”的判决,例如,某厂产品是否合格、某数学模型是否与现实相符等。在这类问题中,往往是要判断手头的数据是否与某假设明显不符,所以也称为显著性检验。