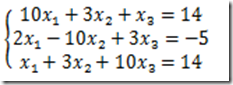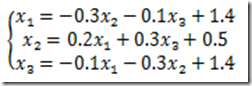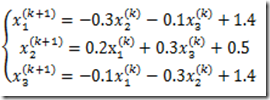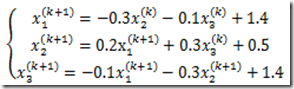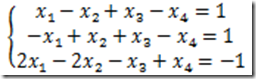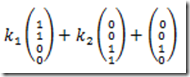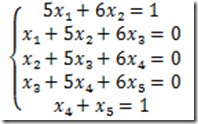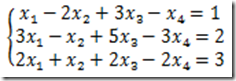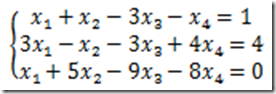【笔记】线性方程组
目标:了解线性方程组的数值解法,掌握求解线性方程组的迭代法的有关原理方法,会用迭代法收敛的有关理论来分析迭代法的收敛性和收敛速度。
工程中许多问题最后都可以转化为求解线性方程组,而且许多数值计算问题(如样条函数、常微分方程数值解、差分方程等)的研究也往往归结为此类问题,因此线性方程组的求解是一个有广泛应用背景的问题。
线性方程组的数值法一般有如下两类:
- 直接法——经过有限次算法求出精确解(实际上由于舍入误差只能得到近似解),最常用的方法是高斯消元法以及矩阵LU分解。
- 迭代法——从初始值出发,用递推的方法,给出近似解序列。最常用的方法是雅克比迭代法和高斯-赛德尔迭代法。
直接法一般适用于系数矩阵A为低阶稠密矩阵(非零元素较多)的情况,而在工程技术和科学计算中常会遇到大型稀疏矩阵(非零元素较少)形式的方程组。迭代法在计算和存储两方面都适合于后一种情况。
计算实验:线性方程组求解
例1 用雅克比迭代法和高斯-赛德尔迭代法解线性方程组
比较两种迭代法的计算结果和收敛速度。
解:将方程组改写为
构造雅克比迭代格式
程序如下:
%雅克比迭代程序
A=[10 3 1;2 -10 3;1 3 10];
b=[14;-5;14];
D=diag(diag(A));
L=tril(A,-1);
U=triu(A,1);
J=-inv(D)*(L+U);
g=inv(D)*b;
x=[0 0 0]';
for i=1:9
x=J*x+g;
xx(i,:)=vpa(x,6);
end
xx
如果构造高斯-赛德尔迭代格式
程序如下:
%高斯-赛德尔迭代程序
A=[10 3 1;2 -10 3;1 3 10];
b=[14;-5;14];
D=diag(diag(A));
L=tril(A,-1);
U=triu(A,1);
G=-inv(D+L)*U;
g=inv(D+L)*b;
x=[0 0 0]';
for i=1:9
x=G*x+g;
xx(i,:)=vpa(x,6);
end
xx
计算结果对照表1(方程组的精确解为x=[1;1;1])。
| k | xT(雅克比迭代) | xT(高斯-赛德尔迭代) |
|
0 1 |
[0,0,0] [ 1.4, 0.5, 1.4] |
[0,0,0] [ 1.4, 0.78, 1.026] |
从表中可以看出,高斯-赛德尔迭代法的收敛速度比雅克比迭代法快。除此之外从迭代格式的形式还可以看出,高斯-赛德尔迭代法需要存储的信息较少,因此占用的存储空间较少。
结果分析:
本问题中,雅克比矩阵的谱半径r(J)=0.3873<1,高斯-赛德尔迭代矩阵的谱半径r(G)=0.1831<1,且r(G)<r(J),所以两种迭代法都收敛,并且高斯-赛德尔迭代法的收敛速度快。
例2 求线性方程组的通解
注:在无穷多解情况下可以用三种方法求得通解:
- rref化为行最简形式以后求解
- 用除法求出一特解,再用null求得一个奇次组的基础解系
- 用符号数学工具箱中的solve求解
解:在指令窗中执行
>> clear;a=[1 -1 1 -1;-1 1 1 -1;2 -2 -1 1];
>> b=[1;1;-1];
>> [rank(a),rank([a,b])]
ans =
2 2
>> %秩相等且小于4,说明有无穷多解
>> % 方法一
>> rref([a,b])
ans =
1 -1 0 0 0
0 0 1 -1 1
0 0 0 0 0
从而原方程等价于x1=x2,x3=x4+1。令x2=k1,x4=k2,求得通解为:
例3 (利用矩阵除法求线性方程组的特解)求方程组
的解。
解:
>> A=[5 6 0 0 0
1 5 6 0 0
0 1 5 6 0
0 0 1 5 6
0 0 0 1 5];
>> B=[1 0 0 0 1]';
>> % 求秩
>> R_A=rank(A)
R_A =
5
>> % 求解
>> X=A\B
X =
2.2662
-1.7218
1.0571
-0.5940
0.3188
这就是方程组的解。
或用函数rref求解:
>> % 由系数矩阵和常数列构成增广矩阵C
>> C=[A B];
>> % 将C化成最简形式
>> R=rref(C)
R =
1.0000 0 0 0 0 2.2662
0 1.0000 0 0 0 -1.7218
0 0 1.0000 0 0 1.0571
0 0 0 1.0000 0 -0.5940
0 0 0 0 1.0000 0.3188
则R的最后一列元素就是所求之解。
例4 (求奇次线性方程组的通解)
在MATLAB中,函数null用来求解零空间,即满足A.X=0的解空间,实际上是求出解空间的一组基(基础解系)。
格式:
- z=null(A) % z的列向量为方程组的正交规范基,满足Z’xZ=I。
- z=null(A,’r’) % z的列向量是方程AX=0的有理基
求解方程组的通解:
解:
>> A=[1 2 2 1;2 1 -2 -2; 1 -1 -4 -3];
>> format rat
>> B=null(A,'r') %求解空间的有理基
B =
2 5/3
-2 -4/3
1 0
0 1
或通过行最简形得到基:
>> R=rref(A)
R =
1 0 -2 -5/3
0 1 2 4/3
0 0 0 0
(与上面结果一致)
写出通解:
>> syms k1 k2
>> X=k1*B(:,1)+k2*B(:,2)
X =
2*k1 + (5*k2)/3
- 2*k1 - (4*k2)/3
k1
k2
例5 (求非奇次线性方程组的通解)
注:非齐次线性方程组需要先判断方程组是否有解,若有解,再去求通解。步骤如下:
- 判断AX=b是否有解,若有解则进行第二步
- 求AX=b得一个特解
- 求AX=0的通解
- AX=b的通解:AX=0的通解+AX=b的一个特解。
求解方程组
解: 在MATLAB中建立M文件
A=[1 -2 3 -1;3 -1 5 -3;2 1 2 -2];
b=[1 2 3]';
B=[A b];
n=4;
R_A=rank(A)
R_B=rank(B)
format rat
% 判断有唯一解
if R_A==R_B&R_A==n
X=A\b
% 判断有无穷解
elseif R_A==R_B&R_A<n
%求特解
X=A\b
% 求AX=0的基础解系
C=null(A,'r')
% 判断无解
else X='Equation no solution'
end
运行后结果显示:
R_A =
2
R_B =
3
X =
Equation no solution
说明:该方程组无解
例6 (较完整)求解方程组的通解:
解:
方法一:在MATLAB中建立如下M文件
A=[1 1 -3 -1;3 -1 -3 4;1 5 -9 -8];
b=[1 4 0]';
B=[A b];
n=4;
R_A=rank(A)
R_B=rank(B)
format rat
if R_A==R_B&R_A==n
X=a\b
elseif R_A==R_B&R_A<n
X=A\b
C=null(A,'r')
else X='Equation no solution'
end
运行结果为:
R_A =
2
R_B =
2
Warning: Rank deficient, rank = 2, tol = 8.8373e-015.
> In fuluA at 11
X =
0
0
-8/15
3/5
C =
3/2 -3/4
3/2 7/4
1 0
0 1
所以原方程的通解为X=k1C[:,1]+k2C[:,2]+X
方法二:用rref求解
>> A=[1 1 -3 -1;3 -1 -3 4;1 5 -9 -8];
>> b=[1 4 0]';
>> B=[A b];
>> C=rref(B)
C =
1 0 -3/2 3/4 5/4
0 1 -3/2 -7/4 -1/4
0 0 0 0 0
对应齐次方程组的基础解系为:e1=[3/2 3/2 1 0]’ , e2=[-3/4 7/4 0 1]’ ;非齐次方程组的特解为:
n*=[5/4 –1/4 0 0]’ .所以原方程组的通解为:X=k1e1+k2e2+n*。