【笔记】MATLAB中的图形（3）

建模与计算实验

数学分析中，特别是积分部分，我们接触了不少有趣的函数，由于其中有的不是一一对应的，用前面提到的方法无法画出他们的图形，这时就只能用参数了。

此外有些图形只能用参数来画，比如空间曲线，在计算机上不接受“两个曲面的交线”这种表示，所以也只能用参数来画。

用参数作图的关键是找出合适的参数表示，尤其是不能有奇点，最好也不要用到开方。这就需要经验的积累。

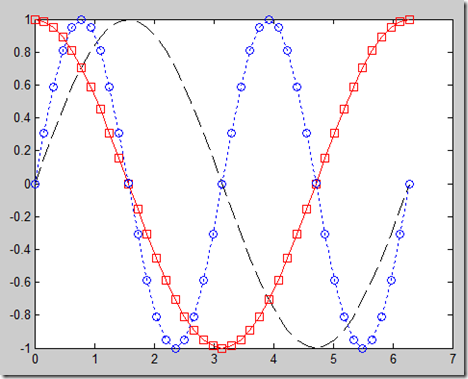
例1 利用函数plot在一个坐标系中画以下几个函数图象，要求采用不同的颜色、不同线型、不同符号标记。函数为x=sin(t),y=cos(t),z=sin(2t),0<=t<=2pi.

程序如下：

>> t=0:pi/20:2*pi;
>> x=sin(t);
>> y=cos(t);
>> z=sin(2*t);
>> plot(t,x,'--k',t,y,'-rs',t,z,':bo')

图形如图1：

图1

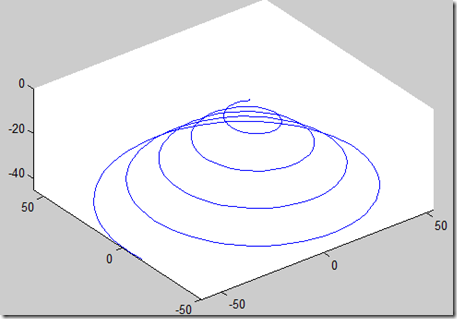
例2 绘制类似田螺线的一条三维螺线（方程自己设计）。

程序如下：

>> t=0:.1:30;
>> x=2*(cos(t)+t.*sin(t));
>> y=2*(sin(t)-t.*cos(t));
>> z=1.5*t;
>> % 取-z是为了图看起来更清晰
>> plot3(x,y,-z)
>> axis equal

图形如图2：

图2

例3 利用函数，绘制一个墨西哥帽子的图形。

程序如下：

>> % 先生成一个网格
>> [a,b]=meshgrid(-8:.5:8);
>> c=sqrt(a.^2+b.^2)+eps;
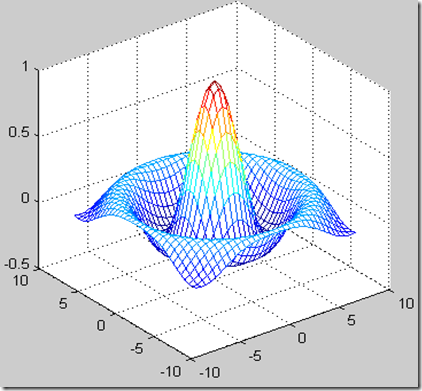
>> z=sin(c)./c;
>> mesh(a,b,z)
>> axis square

图形如图3：

图3

例4 利用surf绘制马鞍面图形(函数为z=(x^2)/9-(y^2)/4)。

程序如下：

>> [x,y]=meshgrid(-25:1:25,-25:1:25);
>> z=x.^2/9-y.^2/4;
>> surf(x,y,z)
>> title('马鞍面')
>> grid off

图形如图4：

图4

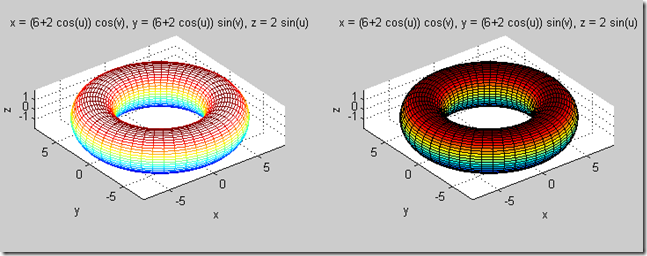
例5 分别用ezmesh和ezsurf各绘制一个圆环面，尝试将两个圆环面放在一个图形界面内，观察他们有什么不同之处。

提示：圆环面的方程为，而圆环面的参数方程为：

程序如下：

% fun1.m
subplot(1,2,1)
ezmesh('(6+2*cos(u))*cos(v)','(6+2*cos(u))*sin(v)','2*sin(u)',([0,2*pi,0,2*pi]))
axis equal
subplot(1,2,2)
ezsurf('(6+2*cos(u))*cos(v)','(6+2*cos(u))*sin(v)','2*sin(u)',([0,2*pi,0,2*pi]))
axis equal

图形如图5：

图5

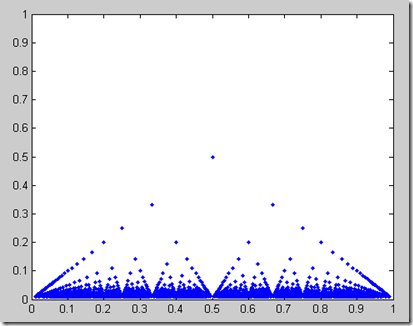
例6 绘制黎曼函数图形。

提示：黎曼函数的定义为

y=

1/q    (当p,q为正整数，p/q为既约分数，x=p/q属于(0,1))

0       (当x=0,1及无理点，x属于[0,1])

程序如下：

% fun2.m
n=100;
x=[];
y=[];
k=1;
for i=2:n
    for j=1:i-1
        if gcd(i,j)==1   %求最大公约数
            x(k)=j/i;
            y(k)=1/i;
            k=k+1;
        end
    end
end
plot(x,y,'.b')
axis([0,1,0,1])

图形如图6：

图6

参考文献:

周品， 等.MATLAB数学建模与仿真.北京：国防工业出版社，2009.