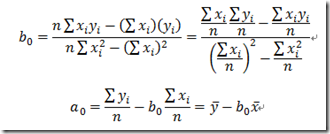【笔记】MATLAB中的图形（2）
三维作图
1、mesh(z)语句
mesh(z)语句可以给出矩阵z元素的三维消隐图，网络表面由z坐标点定义，与前面叙述的x-y平面的线格相同，图形由临近的点连接而成。它可用来显示用其他方式难以输出的包含大量数据的大型矩阵，也可以用来绘制z变量函数。
显示两变量的函数z=f(x,y),第一步需产生特定的行和列的x-y矩阵；然后计算函数在各网格点的值；最后用mesh函数输出。
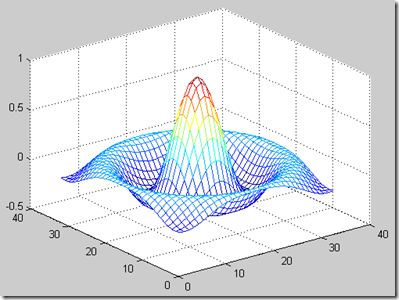
下面我们绘制sin(r)/r函数的图形。建立图形用一下方法：
>> x=-8:.5:8;
>> y=x';
>> x=ones(size(y))*x;
>> y=y*ones(size(y))';
>> R=sqrt(x.^2+y.^2)+eps;
>> z=sin(R)./R;
>> mesh(z) %试运行mesh(x,y,z)，看看与mesh(z)有什么不同？
各语句的意义是：首先建立行向量x，列向量y；然后按向量的长度建立1-矩阵；用向量乘以产生的1-矩阵，生成网格矩阵，他们的值对于与x-y坐标平面；接下来计算各网格点的半径；最后计算函数值矩阵z。用mesh函数即可得到图形（图 1）。
图 1 三维消隐图
第一条语句x的赋值为定义域，在其上估计函数；第三条语句建立一个重复行的x矩阵，第四条语句产生y的响应，第五条语句产生矩阵R（其元素为各网格点到原点的距离）。
另外，上述命令系列中的前4行可以用以下语句替代：
>> [x,y]=meshgrid(-8:0.5:8)
2、与mesh相关的几个函数
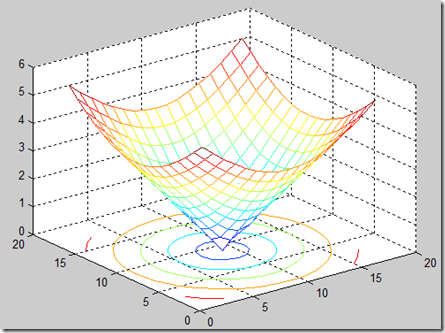
（1）meshc与函数mesh的调用方式相同，只是该函数在mesh的基础上又增加了绘制相应等高线的功能。
例：
>> [x,y]=meshgrid([-4:.5:4]);
>> z=sqrt(x.^2+y.^2);
>> meshc(z)
图 2 meshc图
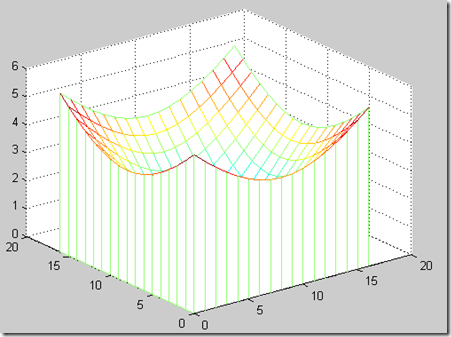
（2）函数meshz与mesh的调用方式也相同，不同的是该函数在mesh函数的作用之上增加了屏蔽作用，即增加了边界面屏蔽。
>> [x,y]=meshgrid([-4:.5:4]);
>> z=sqrt(x.^2+y.^2);
>> meshz(z)
图 3 meshz图
3、其他几个三维绘图函数
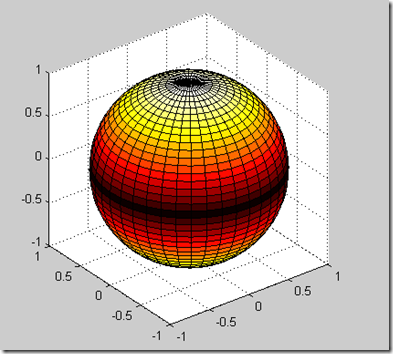
（1）绘制球体sphere，调用格式：
[x,y,z]=sphere(n)
此函数生成三个(n+1)x(n+1)阶的矩阵，再利用函数surf(x,y,z)可生成单位球面。
>> sphere(30) %只绘制球面，不返回值
>> axis square
图4 球面图
若只输入sphere画图，则n=20，为默认值。
（2）surf函数也是MATLAB中常用的三维绘图函数。其调用格式为：
surf(x,y,z,c)
输入参数的设置与mesh相同，不同的是mesh函数绘制的是一网格图，而surf绘制的是着色的三维表面。MATLAB语言对表面进行着色的方法是，在得到相应的网格后，对每一网格依据该网格所代表的节点的色值（由变量c控制），来定义这一网格的颜色。若不输入c，则默认c=z。
例子：
>> % 绘制地球表面的气温分布示意图。
>> [a,b,c]=sphere(40);
>> %求绝对值
>> t=abs(c);
>> surf(a,b,c,t);
>> axis equal
>> colormap('hot')
图 5 等温线示意图
4、图形的控制与修饰
（1）坐标轴的控制函数axis，调用格式如下：
axis（[xmin,xmax,ymin,ymax,zmin,zmax]）
用此命令可以控制坐标轴的范围。
与axis相关的几条命令还有：
axis auto 自动模式，使得图形的坐标范围满足图中一切元素。
axis square 使绘图区为正方形。
axis on 恢复对坐标轴的一切设置。
axis off 取消度坐标轴的一切设置。
axis nanual 以当前的坐标限制图形的绘制。
（2）grid on 在图形中绘制坐标网格。
grid off取消坐标网格。
（3） xlabel、ylabel、zlabel分别为x轴、y轴、z轴添加标注。title为图形添加标题。
以上函数的调用格式大同小异，以xlabel为例:
xlabel;（‘标注文本’，‘属性1’，‘属性2’，…)
这里的属性包括字体大小，字体名，颜色等。
统计回归图
对平面上n个点：(x1,y1),(x2,y2),…,(xn,yn),在平面直线族{y=a+bx|a,b为实数}中寻找 一条直线y=a0+b0x,使得散点到与散点相对应的在直线上的点之间的纵坐标的误差的平方和最小，用微积分方法可得：
所求得的直线y=a0+b0x称为回归直线。
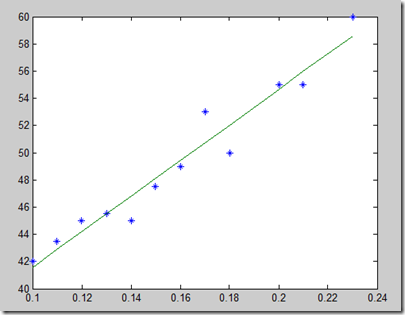
例：已知如下点列，求其回归直线，并计算最小误差平方和。
| x | 0.1 | 0.11 | 0.12 | 0.13 | 0.14 | 0.15 | 0.16 | 0.17 | 0.18 | 0.20 | 0.21 | 0.23 |
| y | 42 | 43.5 | 45 | 45.5 | 45 | 47.5 | 49 | 53 | 50 | 55 | 55 | 60 |
程序如下：
>> x=[0.1 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.20 0.21 0.23];
>> y=[42 43.5 45 45.5 45 47.5 49 53 50 55 55 60];
>> n=length(x);
>> xb=mean(x);
>> yb=mean(y);
>> x2b=sum(x.^2)/n;
>> xyb=x*y'/n;
>> b=(xb*yb-xyb)/(xb^2-x2b);
>> a=yb-b*xb;
>> y1=a+b.*x;
>> plot(x,y,'*',x,y1);
>> serror=sum((y-y1).^2)
serror =
17.4096
图6 回归直线
