无向图三/四元环计数

都是 $O(m\sqrt{m})$ 的。建议使用vector存图以减少cache miss（旧试题那个题不拿vector存貌似过不去，但是我没做）。

三元环

我们首先给每条边定向，规定：对于原图中的每条边，若 $d_u<d_v$ ，或 $d_u=d_v\cap u<v$ （ $u,v$ 是编号， $d$ 是度数）则从 $u$ 到 $v$ 连一条边。

然后所有的三元环一定会长这个样子：（蒯了个图，如果不能显示请扒源代码或者移步cnblogs）

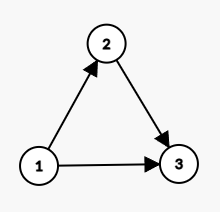
我们可以按照 $1\to 2\to 3$ 的顺序枚举三元环，这样就可以不重不漏。所以我们枚举一个点，把它的所有出点标记，然后扫描所有出点的出点，如果有标记则为三元环。

代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
struct node{
    int v,next;
}edge[200010];
int n,m,t,ans,head[100010],u[200010],v[200010],d[100010],vis[100010];
void add(int u,int v){
    edge[++t].v=v;edge[t].next=head[u];head[u]=t;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&u[i],&v[i]);
        d[u[i]]++;d[v[i]]++;//度数
    }
    for(int i=1;i<=m;i++){
        if(d[u[i]]>d[v[i]]||(d[u[i]]==d[v[i]]&&u[i]>v[i]))swap(u[i],v[i]);
        add(u[i],v[i]);//定向
    }
    for(int x=1;x<=n;x++){
        for(int i=head[x];i;i=edge[i].next)vis[edge[i].v]=x;//标记
        for(int i=head[x];i;i=edge[i].next){
            for(int j=head[edge[i].v];j;j=edge[j].next){
                if(vis[edge[j].v]==x)ans++;//爆扫
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

四元环

同样给每条边定向，原则和上面一样。

然后四元环会变成这个样子：

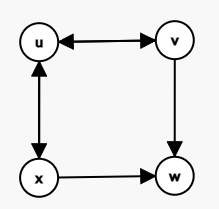
双向边表示两个方向都可以。

我们每次只要从度最大的点出发，枚举出点的出点，每次枚举到一个点就把答案加上那个点的计数器，同时那个点的计数器 $+1$ 。这样就可以计数。当然，我们要求起点与枚举到的点按定向原则比较时起点能向出点连边。

void find(){
    for(int x=1;x<=n;x++){
        for(int i=head[x];i;i=edge[i].next){
            for(int j=head[edge[i].v];j;j=edge[j].next){
                if(d[x]<d[edge[j].v]||(d[x]==d[edge[j].v]&&x<edge[j].v)){
                    ans+=cnt[edge[j].v];cnt[edge[j].v]++;
                }
            }
        }
        for(int i=head[x];i;i=edge[i].next){
            for(int j=head[edge[i].v];j;j=edge[j].next){
                cnt[edge[j].v]=0;
            }
        }
    }
}

然后是复杂度证明：可以证明这样定向的时候每个点的出度都是不超过 $O(\sqrt{m})$ 的。

考虑两种情况：

1. 原图度数不超过 $O(\sqrt{m})$ ，显然出度不超过 $O(\sqrt{m})$ 。
2. 原图度数超过 $O(\sqrt{m})$ ，此时由于整张图的度数是 $O(m)$ 的，因此最多只有 $O(\sqrt{m})$ 个节点度数不小于它，因此只能连 $O(\sqrt{m})$ 条出边。

所以把所有节点扫一遍是 $O(m\sqrt{m})$ 的。