后缀排序

后缀数组（Suffix Array，SA），是一个神奇的用来处理字符串的东西。

首先我们需要一个字符串所有的后缀，后缀 \(i\) 为字符串 \(s\) 的后缀 \(s[i\cdots n]\) 。要求的是两个数组： \(sa[i]\) 为把所有后缀按照字典序排名之后的第 \(i\) 个是哪个后缀， \(rk[i]\) 为后缀 \(i\) 的排名。

然后是构建的方法：

倍增

我们首先对 \(s\) 的所有长度为 \(1\) 的字符排序，得到 \(sa\) 和 \(rk_1\) 。然后使用 \(rk_1[i],rk_1[i+1]\) 作为排序的第一、二关键字，对每个长度为 \(2\) 的子串 \(s[i\cdots i+1]\) 排序，得到 \(sa\) 和 \(rk_2\) 。然后使用 \(rk_2[i],rk_2[i+2]\) 对每个长度为 \(4\) 的子串 \(s[i\cdots i+3]\) 排序，以此类推得到后缀数组。盗个图：

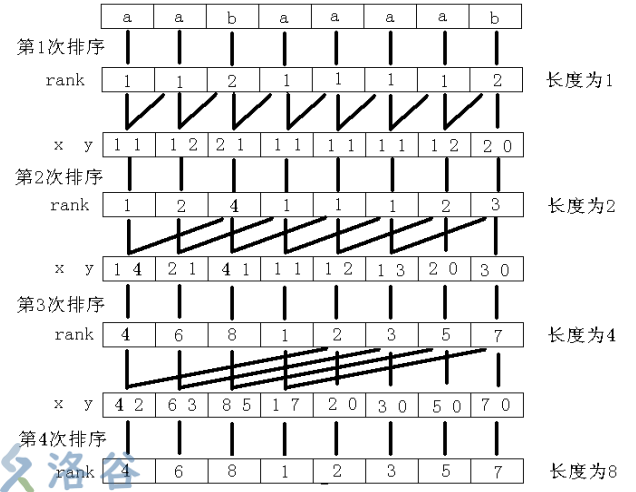
然后我们把上述过程使用基数排序实现就是 \(O(n\log n)\) 的。

void getsa(){
	int m=127;//值域是m
	for(int i=1;i<=n;i++){
		rk[i]=s[i];cnt[rk[i]]++;
	}
	for(int i=1;i<=m;i++)cnt[i]+=cnt[i-1];
	for(int i=n;i>=1;i--)sa[cnt[rk[i]]--]=i;//把所有字符进行第一遍排序
	for(int w=1;;w<<=1){
		int p=0;//开始倍增
		for(int i=n;i>n-w;i--)id[++p]=i;
		for(int i=1;i<=n;i++){
			if(sa[i]>w)id[++p]=sa[i]-w;
		}//按照字典序扫进来
		memset(cnt+1,0,m*4);
		for(int i=1;i<=n;i++){
			key[i]=rk[id[i]];cnt[key[i]]++;
		}//第一关键字
		for(int i=1;i<=m;i++)cnt[i]+=cnt[i-1];
		for(int i=n;i>=1;i--)sa[cnt[key[i]]--]=id[i];//排一遍序
		memcpy(rk2+1,rk+1,n*4);
		p=0;
		for(int i=1;i<=n;i++){
			rk[sa[i]]=(rk2[sa[i]]==rk2[sa[i-1]]&&rk2[sa[i]+w]==rk2[sa[i-1]+w])?p:++p;
		}//第二关键字排序
		if(p==n){
			for(int i=1;i<=n;i++)sa[rk[i]]=i;
			break;
		}
		m=p;
	}
}

一般情况下由于倍增好写，我们使用倍增。

然后有两个 \(O(n)\) 的做法：DC3和SA-IS。DC3因为比倍增难写而且比SA-IS跑得慢所以基本没人写。这里说一下SA-IS。

SA-IS

为了方便，我们在字符串后边新加上一个字符，规定它的字典序最小。然后将后缀分成两类：S型和L型。它们的定义是：

1. 我们加上去的最后一个字符为S型。
2. 如果后缀 \(i\) 比后缀 \(i+1\) 字典序小则 \(i\) 为S型，否则为L型。

我们可以方便地 \(O(n)\) 扫一遍求出一个字符串的所有后缀类型。具体的，我们倒着从后往前扫，直接比较每个字符和后面的字符的大小，如果不相等就可以确定这个后缀的类型。如果相等，那这个后缀的类型就和后面一个后缀的类型相同。

当不相等时正确性显然，相等时我们相当于把这两个字符都去掉，也就是比较 \(s[i+1]\) 和 \(s[i+2]\) ，这个结果已经在 \(i+1\) 位置被算出来了，所以是正确的。

我们有一个推论：如果 \(s[i]=s[j]\) ， \(i\) 为S型， \(j\) 为L型，那么 \(i\) 字典序比 \(j\) 大。显然， \(s[i+1]>s[i]>s[j+1]\) 。

然后是我们整个排序的过程。定义lms（Left-Most-Suffix）型后缀是左边一个是L型的S型后缀。显然一个字符串的lms型后缀数量最多是 \(\frac n2\) 的。lms子串是两个lms型后缀的开头字符中间的子串（包括两个字符）。SA-IS通过将字符串缩成lms子串来缩小范围。举个例子：

Num 1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17
Str m  m  i  i  s  s  i  i  s  s  i  i  p  p  i  i  #
Typ L  L  S  S  L  L  S  S  L  L  S  S  L  L  L  L  S
Lms       *           *           *

子串iissi，iissi，iippii#都是lms子串，离散化一下变成221。这样我们就缩小了数据范围，然后往下递归，递归到lms子串互不相同时就可以开个桶直接计算出sa跑路。

然后是怎么排序lms子串的问题，这个一会再说。我们先看我们已经递归求出下一层的sa，如何计算出本层的sa：诱导排序。

诱导排序大概有几步：

1. 开两个桶分别记录S和L类型每种字符出现的次数。
2. 倒序扫lms，把lms倒序放在sa对应的S型桶末尾。
3. 正序扫sa，如果 \(sa[i]-1\) 的类型是L那么放进对应的L型桶中。
4. 倒序扫sa，如果 \(sa[i]-1\) 的类型是S那么放进对应的S型桶中。

然后关于lms子串的排序，有个结论：乱序的lms诱导排序一遍就有序了。

好了诱导排序有关的东西我都不会证（不过还算挺好写的。

最后一步是怎么对lms离散化的问题。这个其实也很简单，由于lms已经排好序且总长度是 \(O(n)\) 的，所以我们可以看首字母，如果不同直接编号，相同暴力匹配就可以。

于是我们就得到了完整的流程：

1. 确定每个后缀的类型，找出lms类型后缀。
2. 第一遍诱导排序，对lms排序。
3. 对lms离散化。
4. 如果lms互不相同，直接计算sa，否则递归。
5. 恢复lms的位置，诱导排序一遍计算sa。

代码实现难度其实不小（主要容易写太长），加个注释。没有用力卡常。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
string ch;//为了稍微卡卡常用string O(1)计算长度
int n,sa[1000010],rk[1000010],pos[2000010],s[2000010];
int cnt[1000010],cnt1[1000010];
bool tp[2000010];
#define L(x) sa[cnt[s[x]]--]=x;
#define R(x) sa[cnt[s[x]]++]=x;
inline void sa_sort(int pos[],int n,int m,int s[],bool tp[],int num){
	for(int i=1;i<=n;i++)sa[i]=0;
	for(int i=1;i<=m;i++)cnt1[i]=0;//初始化
	for(int i=1;i<=n;i++)cnt1[s[i]]++;
	for(int i=1;i<=m;i++)cnt1[i]+=cnt1[i-1];
	for(int i=1;i<=m;i++)cnt[i]=cnt1[i];
	for(int i=num;i>=1;i--)L(pos[i]);//倒序扫一遍lms放进桶
	for(int i=1;i<=m+1;i++)cnt[i]=cnt1[i-1]+1;
	for(int i=1;i<=n;i++){
		if(sa[i]>1&&tp[sa[i]-1])R(sa[i]-1);//正序扫L
	}
	for(int i=1;i<=m;i++)cnt[i]=cnt1[i];
	for(int i=n;i>=1;i--){
		if(sa[i]>1&&!tp[sa[i]-1])L(sa[i]-1);//倒序扫S
	}
}
void SA_IS(int n,int m,int s[],bool tp[],int pos[]){
	int t=0,num=0;tp[n]=0;
	for(int i=n-1;i>=1;i--){
		tp[i]=(s[i]!=s[i+1])?s[i]>s[i+1]:tp[i+1];
	}//确定S型和L型后缀
	rk[1]=0;
	for(int i=2;i<=n;i++){
		if(tp[i-1]&&!tp[i])pos[++t]=i,rk[i]=t;
		else rk[i]=0;
	}//找到所有lms子串
	sa_sort(pos,n,m,s,tp,t);//诱导排序lms
	for(int i=1,p=0;i<=n;i++){
		if(rk[sa[i]]){
			int x=rk[sa[i]];
			if(num<=1||pos[x+1]-pos[x]!=pos[p+1]-pos[p])num++;
			else{
				for(int j=0;j<=pos[x+1]-pos[x];j++){
					if(s[pos[x]+j]!=s[pos[p]+j]||tp[pos[x]+j]!=tp[pos[p]+j]){
						num++;break;//直接爆扫
					}
				}
			}
			s[n+x]=num;p=x;
		}
	}//离散化
	if(t!=num)SA_IS(t,num,s+n,tp+n,pos+n);//递归向下
	else{
		for(int i=1;i<=t;i++)sa[s[n+i]]=i;//互不相同直接计算
	}
	for(int i=1;i<=t;i++)s[i+n]=pos[sa[i]];
	sa_sort(s+n,n,m,s,tp,t);//归位 诱导排序计算sa
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>ch;
	n=ch.length();
	for(int i=1;i<=n;i++)s[i]=ch[i-1];
	s[++n]=1;
	SA_IS(n--,127,s,tp,pos);
	for(int i=1;i<=n;i++)rk[sa[i]=sa[i+1]]=i;
	for(int i=1;i<=n;i++)cout<<sa[i]<<" ";
	return 0;
}

height数组

\(height[i]=lcp(sa[i],sa[i-1])\) ，即第 \(i\) 名后缀和第 \(i-1\) 名后缀的最长公共前缀。

然后是一个引理： \(height[rk[i]]\ge height[rk[i-1]]-1\) 。借助这个我们可以 \(O(n)\) 求 \(height\) 数组，直接整个指针扫一遍就行了。

void getheight(){
	for(int i=1,k=0;i<=n;i++){
		if(rk[i]==0)continue;
		if(k)k--;
		while(s[i+k]==s[sa[rk[i]-1]+k])k++;
		height[rk[i]]=k;
	}
}

\(height\) 数组用处很多。举个例子，两后缀的最长公共前缀 \(lcp(sa[i],sa[j])=\min_{k=i}^jheight[k]\) 。

别的等我多做点题会另开一篇专说。