杨表

前情提要：前些日子看Clover_BY操前看了蓝书上的一道题：（我操前一直什么也不带）

有 $N$ 个学生合影，站成左端对齐的 $k$ 排，每排分别有 $N_1,N_2,\cdots ,N_k$ 个人，第一排站在最后面，第 $k$ 排站在最前面。学生的身高互不相同，把他们从高到低依次标记为 $1,2,\cdots ,N$ 。在合影时要求每一排从左到右身高递减，每一列从后到前身高也递减，问一共有多少种安排合影位置的方案。

（实际上这个题的 $N$ 是单调递减的）

然后当时就发现了杨表不会的事实。然后当天就补了一发。

杨表是一种精妙的组合结构生成函数的白给。（不知道为什么我bdfs一下一堆杨表的插入元素删除元素的，真的有人会拿杨表维护什么东西吗）

首先是一些别的（长得很像的）东西：Ferrers图（或者叫杨图）。

$$\begin{array}{rl}& 5:◼◼◼◼◼\\ & 4:◼◼◼◼\\ & 2:◼◼\\ & 1:◼\\ & 1:◼\end{array}$$

可以描绘一个整数分拆。或者换成表格的形式：

所以我们首先介绍一下整数分拆。

分拆数

定义：$P_n$ 为将 $n$ 拆分成若干无序正整数之和的方案数。

分拆数有个 OGF 。先枚举拆出哪个数，再枚举拆几个出来。

$$P(x)=\prod _{k=1}\sum _{i=0}{x}^{ik}=\prod _{k=1}\frac{1}{1-x^k}$$

当然你可以 $\ln \exp$ 求，$O(n\log n)$。

如果没有 NTT 模数，我们可以 $O(n^2)$ dp，根号分治可以达到 $O(n\sqrt{n})$。但是我们有更简便的方法，复杂度 $O(n\sqrt{n})$ 且极为简洁。

五边形数定理

内容：

$$\prod _{i=1}(1-x^i)=1+\sum _{i-1}(-1{)}^i{x}^{\frac{i(3i\pm 1)}{2}}$$

上边那个指数就是广义五边形数了。原来的五边形数是没有那个加号的，就像这样：（偷个图）

广义五边形数的生成函数就是分拆数的倒数，那么 $n$ 以内的五边形数是 $O(\sqrt{n})$ 的，就可以暴力递推出 $n$ 以内的分拆数。

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cmath>
using namespace std;
int n,cnt,mod,ans[100010],p[100010];
int main(){
    scanf("%d%d",&n,&mod);ans[0]=1;
    for(int i=1;i*(3*i-1)/2<=n;i++)p[cnt++]=i*(3*i-1)/2,p[cnt++]=i*(3*i+1)/2;
    for(int i=1;i<=n;i++){
        for(int j=0;j<cnt&&p[j]<=i;j++){
            ans[i]=(ans[i]+1ll*(((j>>1)&1)?mod-1:1)*ans[i-p[j]]%mod)%mod;
        }
    }
    printf("%d\n",ans[n]);
    return 0;
}

分拆数是 $O(e^{\sqrt{\frac{20}{3}}n})$ 级别的，也就是通常可以枚举几十级别的整数分拆。

杨表

杨表(Young tableau）是通过用取自某个字母表的符号填充杨氏图的框来获得的，这通常需要是一个全序集和。填入的元素写作 $x_1,x_2,x_3,\cdots$。但为了方便起见，都直接填入正整数。（摘自oi-wiki）

这里我们只讨论标准杨表：用 $1-n$ 共 $n$ 个互不相同的正整数填满整个表，并满足各行各列的数字都严格递增。

对于 $n$ 个方格的标准杨表个数，我们有递推式：

$$\begin{gathered} f(0)=1,f(1)=1 \\ f(n)=f(n-1)+(n-1)\times f(n-2) \end{gathered}$$

等于 $n$ 个点完全图的匹配方案数。前几项是：

$$1,1,2,4,10,26,76,232,764,2620,9496,\cdots$$

还有一种半标准的杨表：可以填入相同数字，列严格递增，行单调不降，则为半标准杨表（这个实际上可以计数，一会说）。

标准杨表的插入算法

对于标准杨表，我们有将一个元素插入它的算法：RSK插入算法。同时，这提供了一个将杨表和排列联系起来的途径。它的步骤是（如果我们要插入 $x$ ）：

1. 从第一行开始，在当前行中找到最小的比 $x$ 大的数 $y$ 。
2. 如果找到，用 $x$ 替换 $y$ ，移动到下一行继续插入 $y$ 。
3. 如果没有找到，直接放在该行末尾。

上图：

删除同理。我们如果删除 $x$ ，则在上一行找到最大的比 $x$ 小的数，用 $x$ 替换，移动到上一行继续删除。

然后我们可以用这个算法往杨表里插入一个排列，同时记录一个表，当第 $i$ 次在某个格子填上数的时候将另一个表的这个格子填上 $i$ ，那么最后这两个杨表的形态是一样的。也就是说，两个大小为 $n$ 的杨表对应一个长度为 $n$ 的排列。也就是说，我们有如下公式（Robinson-Schensted correspondence
定理）：

$$n!=\sum _{\lambda ⊢n}{f}_{\lambda }^2$$

其中 $\lambda ⊢n$ 是 $n$ 的一个整数拆分， $f_{\lambda }$ 是这种拆分在杨表的填法数。

然后关于这个填法数怎么求，我们还有一个公式。

勾长公式

对于杨表的一个方格 $v$ 定义其勾长 $\text{hook}(v)$ 为其同行右边的方格数加上同列下面的方格数，然后再加上自己。

！

然后我们有勾长公式：一个杨表的填法数等于 $n!$ 除以所有方格勾长的乘积。

$$f_{\lambda }=\frac{n!}{\prod _x\text{hook}(x)}$$

所以上面这张杨表的填法数为： $\frac{10!}{7\times 5\times 4\times 3\times 1\times 5\times 3\times 2\times 1\times 1}=288$ 。

于是我们可以通过暴力扫来求勾长。需要用到另一个形式：

$$f_{\lambda }=n!\frac{\prod _{1\le i<j\le m}({\lambda }_i-i-{\lambda }_j+j)}{\prod _{i=1}^m({\lambda }_i+m-i)!}$$

int solve(){
    int ret=1;
    for(int i=1;i<=a[0];i++){
        for(int j=i+1;j<=a[0];j++)ret=1ll*ret*(a[i]-i-a[j]+j+mod)%mod;
    }
    for(int i=1;i<=a[0];i++)ret=1ll*ret*inv[a[i]+a[0]-i]%mod;
    ret=1ll*ret*jc[n]%mod;
    return ret;
}

然后事实上这个可以多项式乘法实现一个 $\log$ 的复杂度计算。我们再变形一下：设 $r_i=a_i+m-i$ ，那么 $f_{\lambda }=n!\frac{\prod _{1\le i<j\le m}(r_i-r_j)}{\prod _{i=1}^m{r}_i}$ 。用一个数组记录 $r_i$ 出现的次数（ $r$ 显然互不相同），如果出现了就记录 $c_r=1$ ，没有就是 $0$ 。然后多项式卷积算出 $g_k=\sum _{i-j=k}{c}_i{c}_j$ ，上面的 $\prod _{1\le i<j\le m}(r_i-r_j)$ 就是 $\prod _{i=1}^n{i}^{g_i}$ 。代码在此不表。怎么暴力怎么算就行。

然后是杨表的一些结论：

1. 杨表第一行的长度就是它对应排列的LIS长度（不一定是排列的LIS）。
2. 杨表第一列的长度是这个排列的LDS（最长下降子序列）长度。
3. 对一个排列和它的杨表，这个排列倒过来的杨表就是这个杨表的转置。
4. 元素比较方式取反，则杨表的形状转置（元素不一定）。
5. 定义一个序列的 $k-\text{LIS}$ 为这个序列的最长的满足LIS长度不超过 $k$ 的子序列。那么它的长度就是这个序列对应杨表的前 $k$ 列长度和。

然后我们可以来水一道题：BJWC2018 最长上升子序列。

题意：求 $n$ 长度排列的LIS期望长度 $\mathrm{mod}998244353$ 。

根据上面的公式，我们知道答案就是

$$\frac{1}{n!}\sum _{\lambda ⊢n}{f}_{\lambda }^2{\lambda }_1$$

暴力枚举整数拆分即可。跑 $60$ 只需要 $0.6\text{s}$ 。

#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;
const int mod=998244353;
int n,ans,a[30],jc[30],inv[30];
int qpow(int a,int b){
    int ans=1;
    while(b){
        if(b&1)ans=1ll*ans*a%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return ans;
}
int solve(){
    int ret=1;
    for(int i=1;i<=a[0];i++){
        for(int j=i+1;j<=a[0];j++)ret=1ll*ret*(a[i]-i-a[j]+j+mod)%mod;
    }
    for(int i=1;i<=a[0];i++)ret=1ll*ret*inv[a[i]+a[0]-i]%mod;
    ret=1ll*ret*jc[n]%mod;
    return ret;
}
void dfs(int x,int mx){
    if(x==0){
        int ret=solve();
        ans=(ans+1ll*ret*ret%mod*a[1]%mod)%mod;
        return;
    }
    for(int i=min(x,mx);i>=1;i--){
        a[++a[0]]=i;
        dfs(x-i,i);
        a[0]--;
    }
}
int main(){
    scanf("%d",&n);jc[0]=inv[0]=1;
    for(int i=1;i<=n;i++){
        jc[i]=1ll*jc[i-1]*i%mod;
        inv[i]=qpow(jc[i],mod-2);
    }
    dfs(n,n);
    printf("%lld\n",1ll*ans*inv[n]%mod);
}

CTSC2017 最长上升子序列
题意：给你一个序列，多次询问，每次求它前 $m$ 个元素的 $k-\text{LIS}$ 。

首先显然将询问离线排序然后逐个插入元素回答询问。

据说这个题暴力维护前缀的杨表可以得到 $95$ 分。然后发现暴力维护的话单次查询最坏是 $O(n\log n)$ 的，考虑优化。

显然杨表行和列最小的一维长度不会超过 $\sqrt{n}$ ，于是我们只需要维护前 $\sqrt{n}$ 行和列，如果列数大于 $\sqrt{n}$ 就把比较方式取反，维护这个杨表的转置就行了，总复杂度 $O(n\sqrt{n}\log n)$ 。

代码比较简明。

#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int n,Q,sq,c[50010],ans[200010],a[50010];
int lowbit(int x){
    return x&-x;
}
void update(int x,int val){
    while(x<=n)c[x]+=val,x+=lowbit(x);
}
int query(int x){
    int sum=0;
    while(x)sum+=c[x],x-=lowbit(x);
    return sum;
}
struct Young{
    int a[310][50010];
    void ins(int x,int val,int id){
        if(x>sq)return;//只维护根号以内的
        int l=1,r=a[x][0]+1;
        while(l<r){
            int mid=(l+r)>>1;
            if(id^(val<=a[x][mid]))r=mid;
            else l=mid+1;
        }//二分第一个大于val的值
        swap(a[x][l],val);
        a[x][0]=max(a[x][0],l);//交换，更新大小
        if(val)ins(x+1,val,id);
        else{
            if(id)update(x,1);//直接更新上去
            else if(l>sq)update(l,1);//如果超过根号说明另一个没法维护 上树状数组
        }
    }
}a1,a2;
struct ques{
    int m,k,id;
    bool operator<(const ques &s)const{
        return m<s.m;
    }
}q[200010];
int main(){
    scanf("%d%d",&n,&Q);
    sq=sqrt(n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1;i<=Q;i++){
        scanf("%d%d",&q[i].m,&q[i].k);q[i].id=i;
    }
    sort(q+1,q+Q+1);
    int pos=0;
    for(int i=1;i<=Q;i++){
        while(pos<q[i].m){
            pos++;
            a1.ins(1,a[pos],0);a2.ins(1,a[pos],1);
        }
        ans[q[i].id]=query(q[i].k);
    }
    for(int i=1;i<=Q;i++)printf("%d\n",ans[i]);
}

随机游走：见这篇博客。

斜杨表

斜杨表就是一个大杨表砍掉一个小杨表。大概长成这样：

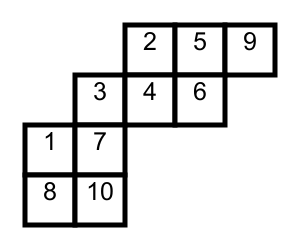
大的为 $\lambda$ ，小的为 $\mu$ 的话，这玩意记作 $\lambda /\mu$ 。

然后是斜半标准杨表计数。一个 $m$ 行，值域 $[1,z]$ 的斜半标准杨表可以表示为 $m$ 条 $({\mu }_i-i,1)\to ({\lambda }_i,z)$ 的不相交路径。如图：

使用LGV引理好像可以解决。

半标准杨表计数

直接上公式（完全不会证明）：（ $h_{\lambda }(i,j)$ 是这个整数拆分对应杨表坐标 $(i,j)$ 的勾长）

$$f_{\lambda }^{\prime }=\prod _{{}_i,j\in \lambda }\frac{n+j-i}{h_{\lambda }(i,j)}=\prod _{1\le i<j\le m}\frac{{\lambda }_i-i-{\lambda }_j+j}{j-i}$$

又一个二百多行的数学博客。格路计数还是不会。