笛卡尔树

笛卡尔树是一种二叉树，每个节点有两个键值 \(x,y\) ，一个满足BST，一个满足堆。上图：

一个性质是如果键值确定那么笛卡尔树是唯一的。

笛卡尔树如果暴力构造很简单：找到整个序列最大/小的一个元素，将它作为当前的根节点，然后左右两边向下递归。但是这并不优秀。事实上我们有 \(O(n)\) 的构建方法。

我们按照下标（满足BST性质的一维）递增顺序将每个元素插入笛卡尔树，同时用一个栈维护一条最右链。那么我们每次插入的元素一定在这条链的末端。再来图：

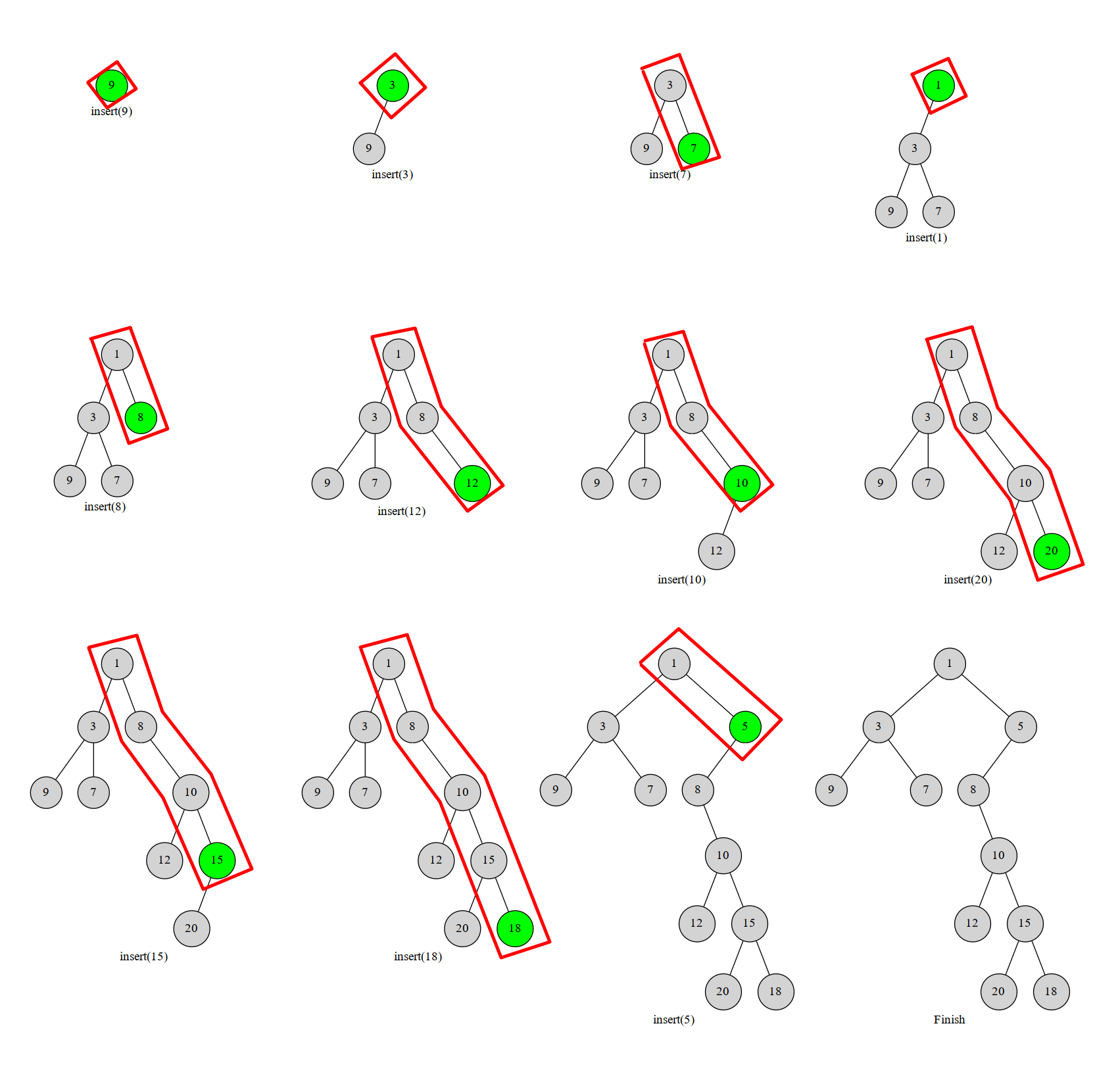
假设我们当前插入 \(a\) ，那么我们找到链上第一个 \(y\) 比 \(y_a\) 更大/小的节点，把它的右儿子设置为 \(a\) ，然后把它原来的右子树改成 \(x\) 的左子树（之前插入的都比 \(x\) 小所以接到左边）。

void build(){
    for(int i=1;i<=n;i++){
        a[i]=read();
        int ret=top;
        while(ret&&a[stk[ret]]>a[i])ret--;
        //在最右链中找第一个权值更小的节点（小根堆）
        if(ret)rson[stk[ret]]=i;
        //改成右儿子
        if(ret<top)lson[i]=s[ret+1];
        //把左儿子接过来
        s[++ret]=i;top=ret;//入栈
    }
}

然后是它的一个小性质：对一个序列建树之后区间 \([l,r]\) 的最大/小值就是笛卡尔树上节点 \(l,r\) 对应点的LCA。可以拿来搞 \(\pm1 \text{RMQ}\) ，还有个东西叫四毛子，以后再说。

别的似乎没什么大用处。

对了还有之前一个考试题，超级加倍 T3。