AC自动机

\(\text{AC}\) 自动机，一般可以处理一类多模式串匹配问题，也可以拿来 \(dp\) 。大概就是 \(\text{kmp}+\text{trie}\) 。

首先我们知道给定单个模式串和单个文本串来匹配可以 \(\text{kmp}\) 。然后现在要多个模式串个单个文本串匹配。而且一个一个搞复杂度会爆炸。那我们就需要构造 \(\text{AC}\) 自动机。

构建

类似 \(\text{kmp}\) 跳 \(next\) 指针的操作， \(\text{AC}\) 自动机也是通过不断地跳 \(fail\) 指针实现多个模式串的匹配的。

首先我们将所有的字符串扔到trie里。然后开始构建我们的 \(fail\) 指针。它的定义是：一个节点的 \(fail\) 指针指向所有模式串前缀中匹配当前状态的最长后缀。

啥没看懂？盗张图。

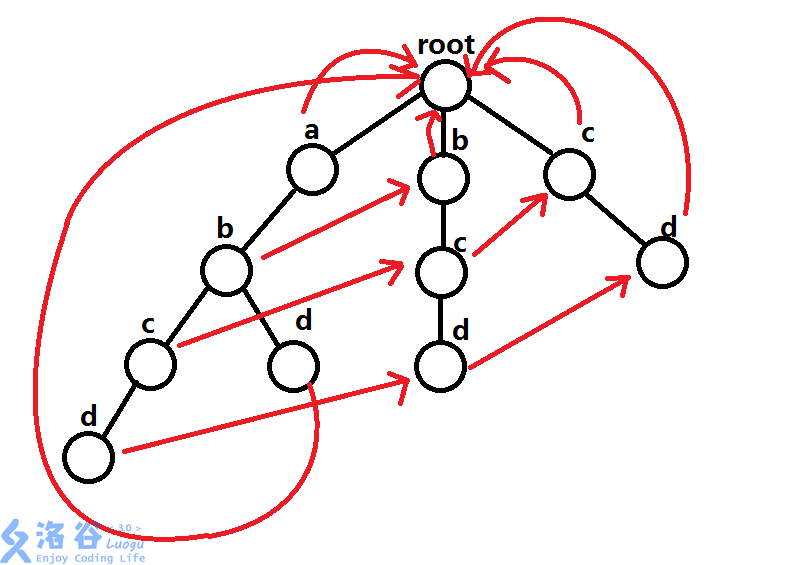
如图所示，以最左边的子树为例，字符串 \(abcd\) 在 \(\text{trie}\) 的最长的后缀是 \(bcd\) ，所以 \(d\) 的 \(fail\) 指针会连到 \(bcd\) 的 \(d\) 上。然而 \(abd\) 在 \(\text{trie}\) 上不存在后缀，所以 \(fail\) 指针指向根节点。其他的同理。容易发现，我们 \(n\) 个节点，有 \(n-1\) 个 \(fail\) 指针（不算根节点自己连自己的），所以所有 \(fail\) 指针构成了一棵树，我们一般称它为 \(fail\) 树。它有一些比较好的性质（一会例题会举例说明）。

然后考虑如何快速构建出整个自动机。暴力找最长后缀的复杂度显然是不能接受的，于是我们考虑一点人类智慧的方法。具体的，我们可以修改一下 \(\text{trie}\) 的结构。

首先我们通过 \(\text{bfs}\) 构造指针。首先将与根节点直接相连的所有节点入队，并将它们的 \(fail\) 指针指向根节点。然后每次取出队头节点 \(x\) 并遍历所有 \(26\) 个子节点（就拿小写字母集举例子）。容易发现该节点的子节点要么存在要么不存在。分类讨论一下：

1. 不存在：我们修改 \(\text{trie}\) 的结构，直接使 \(trie[x][i]=trie[fail[x]][i]\) ,也就是在之前的基础上扩展一个字符。这一步将空余位置连到了 \(fail\) 指针的对应状态，从而使得下次失配的时候如果跳到这个节点那么可以直接找到 \(fail\) 指针，而不需要重复跳。
2. 存在：我们将 \(trie[x][i]\) 的 \(fail\) 指针变成 \(trie[fail[x]][i]\) 。这里我们不需要通过一直跳 \(fail\) 指针来找到最长的后缀，因为我们有上一步修改字典树结构的操作。如果在 \(x\) 失配，则我们会跳转到他的 \(fail\) 指针。而我们用字典树的空余位置直接存下了下一次会跳到哪一个指针，实现了加速。最后将它入队。

如果实在难以理解可以找oiwiki的动图慢慢看，或者自己画一下图。实在不行可以背，反正也挺好背的。

查询其实也很简单，类似 \(\text{trie}\) ，我们每次仍然在原来的字典树上跳，然后每跳到一个节点就跳它的 \(fail\) 指针直到跳空。由于一个节点的 \(fail\) 指针是连到它的最长后缀，所以既然这个串已经出现过了，那 \(fail\) 指针对应的后缀串也是出现过的。

到此，我们切掉了这个板子。

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
int n,num,trie[500010][26],fail[500010];
int cnt[500010];
char s[1000010];
void ins(char s[]){
	int p=0,len=strlen(s);
	for(int i=0;i<len;i++){
		if(!trie[p][s[i]-'a'])trie[p][s[i]-'a']=++num;
		p=trie[p][s[i]-'a'];
	}cnt[p]++;
}
queue<int>q;
void build(){
	for(int i=0;i<26;i++)if(trie[0][i])q.push(trie[0][i]);
	while(!q.empty()){
		int u=q.front();q.pop();
		for(int i=0;i<26;i++){
			if(trie[u][i]){//存在这个节点 更新fail
				fail[trie[u][i]]=trie[fail[u]][i];
				q.push(trie[u][i]);
			}
			else trie[u][i]=trie[fail[u]][i];//不存在则修改trie使得子节点指向之前的失配指针
		}
	}
}
int query(char s[]){
	int p=0,ans=0,len=strlen(s);
	for(int i=0;i<len;i++){
		p=trie[p][s[i]-'a'];
		for(int j=p;j&&cnt[j]!=-1;j=fail[j]){//暴力跳所有的fail指针
			ans+=cnt[j];cnt[j]=-1;
		}
	}
	return ans;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%s",s);ins(s);
	}build();
	scanf("%s",s);
	printf("%d",query(s));
	return 0;
}

然后那个加强版的其实也可以过了，就是小修小补一下。记录文本串跳 \(fail\) 指针的时候每个节点被跳到的次数，然后统计所有字符串结尾的节点被跳过多少次即可。

然而这样是过不去那个二次加强版的。这时候就要用到之前提到的 \(fail\) 树。它有一个美妙的性质：如果对于一个节点 \(x\) ，它的父亲是 \(fail[x]\) ，那么考虑它子树的所有点在我们 \(\text{query}\) 函数中被扫到时都会使 \(x\) 被跳到一次。所以我们直接在原来的字典树里跑一个裸的查询，并记录每个节点的遍历次数（由于我们魔改过了字典树所以是可以扫完整个文本串的），然后从所有的叶子开始对整棵树跑一遍拓扑排序，最后找到每个字符串最后一个节点被扫多少次即可。

void query(char s[]){
	int p=0,len=strlen(s);
	for(int i=0;i<len;i++){
		p=trie[p][s[i]-'a'];
		ans[p]++;
	}
}
void tuopu(){
	for(int i=1;i<=num;i++){
		if(ind[i]==0)q.push(i);
	}	
	while(!q.empty()){
		int u=q.front();q.pop();
		cnt[vis[u]]=ans[u];
		ind[fail[u]]--;
		ans[fail[u]]+=ans[u];
		if(ind[fail[u]]==0)q.push(fail[u]);
	}
}

来点简单应用。

P5231 玄武密码

题意：给你一堆模式串和一个文本串，求每个模式串在文本串上匹配的最长前缀。

直接把所有模式串扔进AC自动机，然后跑一遍文本串的匹配并记录能跳到的所有节点，最后在字典树上查询一遍所有模式串即可。

P2444 病毒

题意：给一堆 \(01\) 串，判断是否存在无限长的一个 \(01\) 串满足这些模式串没有一个在这个无限长的串中出现。

\(\text{AC}\) 自动机有一个套路：每个节点可以继承 \(fail\) 指针的状态。因为如果这个节点出现过，那么 \(fail\) 指针所对应的字符串（后缀）也必然出现过。所以当前串的状态可以继承 \(fail\) 指针的状态。这个题就可以标记所有串在字典树上的最后一个节点，然后跑 \(\text{AC}\) 自动机的时候加一句话就行。

void build(){
	for(int i=0;i<2;i++){
		if(trie[0][i])q.push(trie[0][i]);
	}
	while(!q.empty()){
		int u=q.front();q.pop();
		for(int i=0;i<2;i++){
			if(trie[u][i]){
				fail[trie[u][i]]=trie[fail[u]][i];
				cnt[trie[u][i]]|=cnt[fail[trie[u][i]]];//就这一句 cnt是是否被标记
                //因为如果fail被标记那u一定被标记
				q.push(trie[u][i]);
			}
			else trie[u][i]=trie[fail[u]][i];
		}
	}
}

然后记录答案的时候直接在 \(\text{trie}\) 上 \(dfs\) ，我们需要找出一个从根节点开始可以不经过任何被标记的节点而到达的环。

void dfs(int x){
	if(v[x]){
		jud=true;return;
	}
	if(cnt[x])return;
	v[x]=cnt[x]=true;
	if(trie[x][0]&&!cnt[trie[x][0]])dfs(trie[x][0]);
	if(trie[x][1]&&!cnt[trie[x][1]])dfs(trie[x][1]);
	v[x]=false;
}

P2414 阿狸的打字机

题意：给若干模式串，多次询问，每次询问求第 \(x\) 个串在第 \(y\) 个串中出现多少次。

根据我们 \(fail\) 树的性质， \(x\) 在 \(y\) 中出现多少次就是 \(x\) 的最后一个节点在 \(fail\) 树的子树中 \(y\) 的节点有多少个。可以简单\(dfs\)序解决。

然后是另一个大头： \(\text{AC}\)上 \(dp\) 。

这个一般有一个套路：继承状态然后设 \(dp[i][j]\) 为 \(i\) 长度的串，走到自动机的第 \(j\) 个节点的答案。举个例子：

P4052 文本生成器

题意：给定若干模式串，求有多少 \(n\) 长度串包含任意模式串。

简易容斥一下，变成所有的（ \(26^n\) ）减去不包含任意模式串的。然后按照上面的设置状态，初值显然 \(dp[0][0]=1\) 。顺便标记所有的字符串最后一个节点并按 \(fail\) 转移。然后有一个显然的 \(dp\) 式子：（设 \(u\) 是某个节点， \(v\) 是它在字典树上的一个子节点）

\[dp[i][v]=\sum dp[i-1][u](u没有被标记) \]

意义显然，如果没有被标记就可以添加一个特定字符到下一个状态。只上 \(dp\) 部分代码算了。

for(int i=1;i<=m;i++){
	for(int j=0;j<=cnt;j++){
		if(!vis[j]){
			for(int k=0;k<26;k++){
				if(!vis[trie[j][k]])dp[i][trie[j][k]]=(dp[i][trie[j][k]]+dp[i-1][j])%mod;
			}
		}
	}
}

P4025 密码

题意：懒得说了。只讲解 \(dp\) 部分。

看数据范围一眼状压。所以设 \(dp[i][j][s]\) 为 \(i\) 长度到第 \(j\) 个节点，所包含字符集为 \(s\) 的方案数，然后可以在构建自动机的时候继承得到每个节点的状态。然后式子就显然了： \(dp[i][v][s|st[v]]=\sum dp[i-1][u][s]\) 。