李超线段树

线段树的一种变体。可以用来维护区间内一堆线段（就是一次函数）的取值问题（全局修改是一个\(\log\)的但是区间修改是两个\(\log\)的，因为线段树一个\(\log\)打标记一个\(\log\)）。

比如说板子。

题意：维护区间的一大堆线段的最大值。

李超线段树的大体思路是维护一个区间中点处的优势线段（感性理解就是取值最大的线段，但不完全是）。

考虑线段树的两个操作：修改和查询。

先看修改。我们类似普通线段树进行修改。因为只能单点查询所以我们不需要pushup操作。如果暴力修改，我们考虑这段区间中点处的线段取值。如果增加的线段比原来的线段大，将它们交换。

现在考虑如何打标记。盗张图：

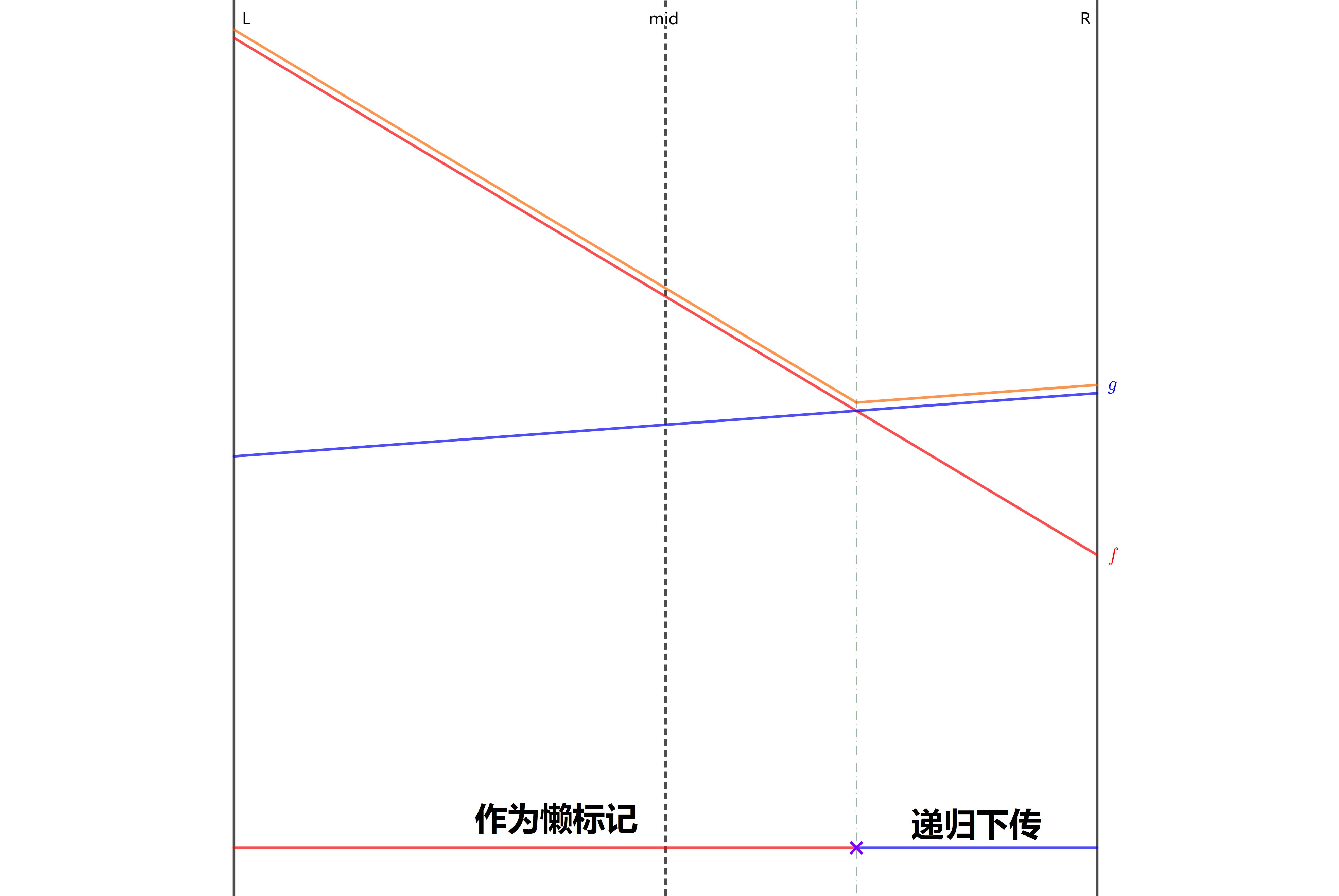
我们发现这个标记不好处理，因为中点处更优不一定全局更优。所以我们递归下传标记就行了。由于一条线段最多更新两个子树中的一个，所以标记下传的复杂度是一个\(\log\)的。

具体来说整个过程，我们找到一条线段\(a\)在中点处比当前线段\(b\)的取值更小。此时我们比较这两条线段在区间两个端点处的取值，如果\(a\)更大就递归下传，如果\(b\)更大直接不管。这样代码就非常好写。

然后是查询，我们容易发现李超线段树的修改操作使得它不支持普通的懒标记下传方法，即跟着修改/查询一起下传。所以我们可以使用标记永久化，查询一个位置时统计所有覆盖当前位置的答案的贡献。

随手上个代码。

#include <cstdio>
#include <algorithm>
#include <iostream>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
const double eps=1e-9;
const int mod1=39989,mod2=1000000000;
int n,ans,cnt;
struct line{
    double k,b;
}l[100010];
struct node{
    int l,r,id;
}tree[160010];
double y(int id,int x){
    return l[id].k*x+l[id].b;
}
int cmp(double x,double y){return x-y>eps?1:y-x>eps?-1:0;}
void pushtag(int rt,int id){
    int mid=(tree[rt].l+tree[rt].r)>>1;
    if(cmp(y(id,mid),y(tree[rt].id,mid))==1)swap(id,tree[rt].id);
    //当前优势线段取得取值更大的线段
    int ret=cmp(y(id,tree[rt].l),y(tree[rt].id,tree[rt].l));
    if(ret==1||(!ret&&id<tree[rt].id))pushtag(lson,id);
    //左端点下传
    ret=cmp(y(id,tree[rt].r),y(tree[rt].id,tree[rt].r));
    if(ret==1||(!ret&&id<tree[rt].id))pushtag(rson,id);
    //右端点下传
}
void build(int rt,int l,int r){
    tree[rt].l=l;tree[rt].r=r;
    if(l==r)return;
    int mid=(l+r)>>1;
    build(lson,l,mid);build(rson,mid+1,r);
}
void update(int rt,int l,int r,int id){
    if(l<=tree[rt].l&&tree[rt].r<=r){
        pushtag(rt,id);return;
    }
    int mid=(tree[rt].l+tree[rt].r)>>1;
    if(l<=mid)update(lson,l,r,id);
    if(mid<r)update(rson,l,r,id);
}
struct stu{
    double y;int id;
};
stu maxx(stu a,stu b){
    if(cmp(a.y,b.y)==-1)return b;
    else if(cmp(a.y,b.y)==1)return a;
    else return a.id<b.id?a:b;
}//比较两条线段取值
stu query(int rt,int pos){
    stu val={y(tree[rt].id,pos),tree[rt].id};//标记永久化
    if(tree[rt].l==tree[rt].r)return val;
    int mid=(tree[rt].l+tree[rt].r)>>1;
    if(pos<=mid)return maxx(val,query(lson,pos));
    else return maxx(val,query(rson,pos));
}
int main(){
    scanf("%d",&n);
    build(1,1,mod1);
    while(n--){
        int od;scanf("%d",&od);
        if(od==1){
            int x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            x1=(x1+ans-1+mod1)%mod1+1;
            x2=(x2+ans-1+mod1)%mod1+1;
            y1=(y1+ans-1+mod2)%mod2+1;
            y2=(y2+ans-1+mod2)%mod2+1;
            if(x1>x2)swap(x1,x2),swap(y1,y2);
            cnt++;
            if(x1==x2){
                l[cnt].k=0;l[cnt].b=max(y1,y2);
            }
            else{
                l[cnt].k=1.0*(y2-y1)/(x2-x1);
                l[cnt].b=y1-l[cnt].k*x1;
            }//一次函数
            update(1,x1,x2,cnt);
        }
        else{
            int x;scanf("%d",&x);
            x=(x+ans-1+mod1)%mod1+1;
            ans=query(1,x).id;
            printf("%d\n",ans);
        }
    }
}

P.S.其实你没必要把树建出来，但是我觉得这样可读性比较强就建了一手（

其实我不太习惯把区间左右端点跟着函数下传，都是先建一手树，这就导致常数贼大（