多项式全家桶

置顶：Delov大佬建议一定要封装多项式板子，不然日后会非常痛苦。

upd：换了多项式的板子。前面的不打算动了，毕竟不想把推导重修一遍。也作为一个常数较大但是较好理解的实现。跑的快的多项式板子在后半段。

对了如果直接找板子的话可以看挑战多项式的提交记录。没有封装。

多项式全家桶要来了。注意数组开4倍。

关于多项式代码实现细节：

1. 数组一定要清空！数组一定要清空！数组一定要清空！
2. 如果你觉得什么时候应该预处理一下当前长度的反转操作那就处理一下，要不然容易爆炸。

跑的不快的板子

多项式乘法逆

这个oiwiki上有三个方法，这里只说主流的倍增。

首先我们要求\(F(x)\)在\(\mod x^n\)意义下的逆元\(F^{-1}(x)\)，假设现在我们已经知道了它在模\(x^{\lceil\frac n2\rceil}\)意义下的逆元\(F_0^{-1}(x)\)，这样我们就可以递归求解逆元，边界是\(f^{-1}_0\)为\(f_0\)的逆元。

我们有

\[F(x)\times F^{-1}(x)\equiv 1(\mod x^{\lceil\frac n2\rceil}) \]

\[F(x)\times F_0^{-1}(x)\equiv 1(\mod x^{\lceil\frac n2\rceil}) \]

上下减一下，有：

\[F(x)\times (F^{-1}(x)-F_0^{-1}(x))\equiv 0(\mod x^{\lceil\frac n2\rceil}) \]

也就是

\[F^{-1}(x)-F_0^{-1}(x)\equiv 0(\mod x^{\lceil\frac n2\rceil}) \]

两边平方：

\[F^{-2}(x)-2F^{-1}(x)F_0^{-1}(x)+F_0^{-2}(x)\equiv 0(\mod x^n) \]

\[F^{-2}(x)\equiv F_0^{-1}(x)(2F^{-1}(x)-F_0^{-1}(x))(\mod x^n) \]

\[F^{-1}(x)\equiv F_0^{-1}(x)(2-F(x)F_0^{-1}(x))(\mod x^n) \]

递归即可，复杂度根据主定理是\(O(n\log n)\)。上个代码。

void getinv(int n,int a[],int b[]){
    if(n==1){
        b[0]=qpow(a[0],mod-2);
        return;
    }
    getinv((n+1)>>1,a,b);
    wl=1;get(n<<1);
    for(int i=0;i<n;i++)c[i]=a[i];
    for(int i=n;i<wl;i++)c[i]=0;
    ntt(b,wl,1);ntt(c,wl,1);
    for(int i=0;i<wl;i++)b[i]=1ll*(2-1ll*b[i]*c[i]%mod+mod)%mod*b[i]%mod;
    ntt(b,wl,-1);
    for(int i=n;i<wl;i++)b[i]=0;
}
int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++)scanf("%d",&a[i]);//要空出来一位 因为得清空
    getinv(n,a,b);
    for(int i=0;i<n;i++)printf("%d ",b[i]);
    return 0;
}

多项式对数函数

多项式对数函数由麦克劳林级数定义为：

\[\ln(F(x))=-\sum_{i=1}\frac{(1-F(x))^i}{i} \]

这个比较好搞。设\(G(x)=\ln F(x)\)，对两边求导，可以得到：

\[G'(x)=\frac {F'(x)}{F(x)} \]

然后求出来\(F(x)\)的逆元乘一下再积个分就行了。多项式的导数和积分和普通函数的一样。

void dao(int f[],int n){
	for(int i=1;i<n;i++)f[i-1]=1ll*f[i]*i%mod;
	f[n-1]=0;
}
void jifen(int f[],int n){
	for(int i=n;i>=1;i--)f[i]=1ll*f[i-1]*qpow(i,mod-2)%mod;
	f[0]=0;
}
void getln(int n,int a[],int b[]){
    for(int i=0;i<(n<<2);i++)b[i]=0;
    getinv(n,a,b);
    wl=1;get(n<<1);
    for(int i=0;i<n;i++)c[i]=a[i];
    for(int i=n;i<wl;i++)c[i]=0;
    dao(c,wl);
    ntt(c,wl,1);ntt(b,wl,1);
    for(int i=0;i<wl;i++)b[i]=1ll*c[i]*b[i]%mod;
    ntt(b,wl,-1);
    jifen(b,wl);
}

多项式指数函数

多项式指数函数同样是麦克劳林级数定义为：

\[\exp(F(x))=\sum_{i=0}\frac{F(x)^i}{i!} \]

这个不太好搞，因为你不管怎么求导积分它都带着个\(e^{F(x)}\)。这时候我们需要一个神奇的数学方法。

前置芝士：牛顿迭代法（Newton's Method）

这是一个已知一个函数\(g(x)\)，求满足\(g(F(x))\equiv 0(\mod x^n)\)的多项式\(F(x)\)的方法。它的原理是根据切线斜率来逐步逼近答案。让我盗张图。

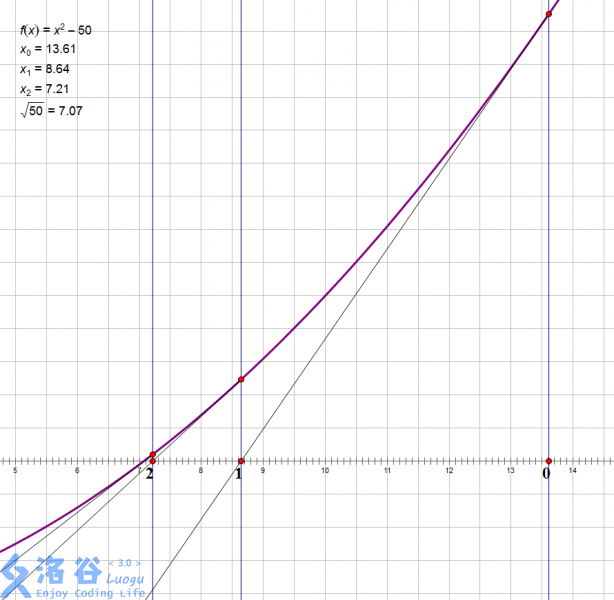
如图所示，我们一步步用切线的斜率找到切线斜率的零点，然后用这个零点继续迭代，最终得到一个较为精确的近似值。而这个套路式出奇地简单：

\[\Huge F_n(x)=F_{n-1}(x)-\frac {g(F_{n-1}(x))}{g'(F_{n-1}(x))} \]

它的重要性可以从字号看出来

这个东西非常重要，可以省去很多思维的难度。而且它是平方收敛的，也就是它迭代次数也不多。还有一个结论是多项式牛顿迭代的时候每次的逼近位数会翻倍，也就是从\(x^{\lceil \frac n2 \rceil}\)变成\(x^n\)。

我们使用牛顿迭代解决多项式\(\exp\)的问题。具体的，我们设一个要求出的多项式（假如说就叫\(G(x)\)），那么我们要解这么一个东西

\[G(x)=e^{F(x)} \]

我们再来说一句废话：

\[G(x)-e^{F(x)}=0 \]

我们考虑把我们要求的多项式看成自变量，把剩余的所有东西看成我们比较方便求的常量，那这就是一个以\(G(x)\)为自变量的函数，设成\(f(x)\)。我们要求的就是它的零点。

然而我们仍然带着一个\(e\)的次幂。考虑如何把它搞成比较方便求的量，看到\(e\)容易想到\(\ln\)。于是对这个函数取个\(\ln\)：

\[f(G(x))=\ln G(x)-F(x) \]

这样就可以牛迭了。注意牛迭的时候所有除自变量外的其他变量都要看做常数，求导的时候直接去掉。

\[\begin{aligned} G(x)&=G_0(x)-\frac {\ln G_0(x)-F(x)}{\frac 1{G_0(x)}}\\ &=G_0(x)(1-\ln G_0(x)+F(x)) \end{aligned}\]

类似地上个代码。

void getexp(int n,int a[],int b[]){
    if(n==1){
        b[0]=1;return;
    }
    getexp((n+1)>>1,a,b);
    getln(n,b,lnb);
    wl=1;get(n<<1);
    lnb[0]=(1-lnb[0]+a[0]+mod)%mod;
    for(int i=1;i<n;i++)lnb[i]=(a[i]-lnb[i]+mod)%mod;
    for(int i=n;i<wl;i++)b[i]=lnb[i]=0;
    ntt(lnb,wl,1);ntt(b,wl,1);
    for(int i=0;i<wl;i++)b[i]=1ll*b[i]*lnb[i]%mod;
    ntt(b,wl,-1);
    for(int i=n;i<wl;i++)b[i]=0;
}

多项式快速幂

首先套路考虑把指数拉下来，也就是两边都取个\(\ln\)。于是变成\(\ln G(x)=k\ln F(x)\)，然后取个\(\exp\)即可。注意因为我们首先对两边取了个\(\ln\)（没有在模意义下），所以导致这个\(k\)是要\(\mod 998244353\)的，不是\(\mod 998244352\)。

void getpow(int n,int a[],int b[],int k){
    getln(n,a,lnb);
    for(int i=0;i<n;i++)a[i]=1ll*lnb[i]*k%mod,lnb[i]=0;
    getexp(n,a,b);
}

然后洛谷这题还有个加强版，常数项不一定是\(1\)了所以\(\ln\)不好搞。我们可以找到最低的不为 \(0\) 的一项，然后把这一项连带着系数作为公因式提出来（就是乘个逆元然后系数平移一下），对这个式子进行普通快速幂，然后把原来消掉的指数乘个幂次补回来就行了。记得特判全是 \(0\) 的情况，还有还原幂次的时候要倒着扫。还有一点就是这个提出来的幂次的系数快速幂是对 \(\varphi(mod)\) 取模。

void getpow(int n,int a[],int b[],int k1,int k2){
    if(a[0]==0&&k3>=n)return;
    int pos;
    for(int i=0;i<n;i++){
        if(a[i]){
            pos=i;break;
        }
    }
    if(1ll*pos*k1>=n)return;
    int inv=qpow(a[pos],mod-2),p=qpow(a[pos],k2);
    for(int i=0;i<n;i++)a[i]=1ll*a[i+pos]*inv%mod;
    getln(n,a,lnb);
    for(int i=0;i<n;i++)a[i]=1ll*lnb[i]*k1%mod,lnb[i]=0;
    getexp(n,a,b);
    pos*=k1;
    for(int i=n-1;i>=pos;i--)b[i]=1ll*b[i-pos]*p%mod;
    for(int i=0;i<pos;i++)b[i]=0;
}
char s[100010];
int main(){
    scanf("%d%s",&n,s);
    int len=strlen(s);
    for(int i=0;i<len;i++){
        k1=(10ll*k1+s[i]-'0')%mod;
        k2=(10ll*k2+s[i]-'0')%(mod-1);
    }
    for(int i=0;i<min(7,len);i++)k3=10ll*k3+s[i]-'0';
    for(int i=0;i<n;i++)scanf("%d",&a[i]);
    getpow(n,a,b,k1,k2);
    for(int i=0;i<n;i++)printf("%d ",b[i]);
    return 0;
}

多项式开根

首先你可以取个 \(\ln\) 然后乘 \(\frac 12\) 最后 \(\exp\) 回去（当然常数大的要命而且没法处理 \(0\) 次项不为 \(1\) 的情况）。常用的方法还是考虑倍增。

仍然假设我们求出了模 \(x^{\lceil \frac n2\rceil}\) 意义下的答案 \(F_0(x)\) ,我们需要求出模 \(x^n\) 意义下的答案 \(F_1(x)\) 。那么我们有：

\[\begin{aligned} F(x)&\equiv \sqrt{F_0(x)}\pmod{x^{\lceil \frac n2\rceil}}\\ F^2(x)&\equiv {F_0(x)}\pmod{x^{\lceil \frac n2\rceil}}\\ F_1(x)&\equiv F_0(x)\pmod{x^{\lceil \frac n2\rceil}}\\ (F_1(x)-F_0(x))^2&\equiv 0\pmod {x^n}\\ F_1^2(x)-2F_1(x)F_0(x)+F_0^2(x)&\equiv 0\pmod{x^n}\\ F(x)-2F_1(x)F_0(x)+F_0^2(x)&\equiv 0\pmod{x^n}\\ F_1(x)&\equiv \frac{F(x)+F_0^2(x)}{2F_0(x)} \end{aligned} \]

大力模拟。记得清空。

void getsqrt(int n,int a[],int b[]){
    if(n==1){
        b[0]=1;return;
    }
    getsqrt((n+1)>>1,a,b);
    for(int i=0;i<wl;i++)inv[i]=0;
    getinv(n,b,inv);
    get(n<<1);
    for(int i=0;i<n;i++)c[i]=a[i];
    for(int i=n;i<wl;i++)c[i]=0;
    ntt(c,wl,1);ntt(b,wl,1);ntt(inv,wl,1);
    for(int i=0;i<wl;i++)b[i]=1ll*(1ll*c[i]*inv[i]%mod+b[i])%mod*inv2%mod;
    ntt(b,wl,-1);
    for(int i=n;i<wl;i++)b[i]=0;
}

这玩意有个加强版，但是需要二次剩余（而且最近二次剩余板子撤掉了）。所以先咕着。

多项式除法

首先我们因为有个余数所以没法直接求逆了事。所以考虑怎么把这个余数消掉。

设 \(F(x)\) 的度数为 \(n\) ，有变换 \(F_R(x)= x^nF(\frac 1x)\) 。容易发现这就是把 \(F(x)\) 的系数反转。

推式子：（假设我们需要算出 \(F(x)/G(x)\) 的商 \(Q(x)\) 和余数 \(R(x)\) ）

\[\begin{aligned} F(x)&=Q(x)\times G(x)+R(x)\\ F(\frac 1x)&=Q(\frac 1x)\times G(\frac 1x)+R(\frac 1x)\\ x^nF(\frac 1x)&=x^{n-m}Q(\frac 1x)\times x^mG(\frac 1x)+x^{n-m+1}\times x^{m-1}R(\frac 1x)\\ F_R(x)&=Q_R(x)\times G_R(x)+x^{n-m+1}R_R(x)\\ F_R(x)&=Q_R(x)\times G_R(x)\pmod {x^{n-m+1}}\\ Q_R(x)&=F_R(x)\times G_R^{-1}(x)\pmod {x^{n-m+1}} \end{aligned} \]

直接求逆得到 \(Q(x)\) ，然后根据 \(F(x)=Q(x)\times G(x)+R(x)\) 求出 \(R(x)\) 。

void getdiv(int n,int m,int a[],int b[],int q[],int res[]){
    for(int i=0;i<=n;i++)q[n-i]=a[i];
    for(int i=0;i<=m;i++)f[m-i]=b[i];
    getinv(n-m+1,f,inv);
    get(n<<1);
    ntt(q,wl,1);ntt(inv,wl,1);
    for(int i=0;i<wl;i++)q[i]=1ll*q[i]*inv[i]%mod;
    ntt(q,wl,-1);
    for(int i=n-m+1;i<wl;i++)q[i]=0;
    reverse(q,q+n-m+1);
    ntt(b,wl,1);ntt(q,wl,1);
    for(int i=0;i<wl;i++)b[i]=1ll*b[i]*q[i]%mod;
    ntt(b,wl,-1);ntt(q,wl,-1);
    for(int i=0;i<m;i++)res[i]=(a[i]-b[i]+mod)%mod;
}

多项式平移

已知 \(F(x)\) ，求 \(F(x+c)\) ， \(c\) 是常数。

考虑二项式定理展开：

\[\begin{aligned} F(x+c)&=\sum_{i=0}^na_i(x+c)^i\\ &=\sum_{i=0}^na_i\sum_{j=0}^i\binom ij c^{i-j}x^j\\ &=\sum_{j=0}^nx^j\sum_{i=j}^n\binom ij a_ic^{i-j}\\ &=\sum_{j=0}^n\frac{x^j}{j!}\sum_{i=j}^na_ii!\frac{c^{i-j}}{(i-j)!} \end{aligned} \]

一次卷积。

void move(int a[],int n,int k,int b[]){
    get(n<<1);int ret=1;
    for(int i=0;i<n;i++,ret=1ll*ret*k%mod)c[i]=1ll*a[i]*jc[i]%mod,b[i]=1ll*ret*inv[i]%mod;
    for(int i=n;i<wl;i++)b[i]=c[i]=0;
    reverse(c,c+n);
    ntt(b,wl,1);ntt(c,wl,1);
    for(int i=0;i<wl;i++)b[i]=1ll*b[i]*c[i]%mod;
    ntt(b,wl,-1);
    reverse(b,b+n);
    for(int i=0;i<n;i++)b[i]=1ll*b[i]*inv[i]%mod,c[i]=0;
    for(int i=n;i<wl;i++)b[i]=0;
}

连续点值平移

考虑拉格朗日插值：

\[\begin{aligned} &f(m+i)\\ =&\sum_{j=0}^nf(j)\prod_{k\neq j}\frac{m+i-j}{j-k}\\ =&\frac{(m+i)!}{(m-n-1+i)!}\sum_{j=0}^n\frac{f(j)(-1)^{n-j}}{j!(n-j)!}\frac 1{m+i-j} \end{aligned} \]

后边看着就很卷积。那 \(a_i=\dfrac{f(i)(-1)^{n-i}}{i!(n-i)!}\)，\(b_{i-j}=\dfrac 1{m+i-j}\)。然而发现上界是 \(n\) 不是 \(i\)，那把整个序列往后挪 \(n\) 位，让 \(f(m+i)\) 落在 \(n+i\) 位置上。这样 \(b_{i-j+n}=\dfrac 1{m+i-j}\)，即 \(b_i=\dfrac 1{m-n+i}\)。卷就行了。

void move(int n,int m,int f[],int g[]){
    jc[0]=mjc[0]=inv[0]=minv[0]=1;
	for(int i=1;i<=2*n+1;i++)jc[i]=1ll*jc[i-1]*i%mod,mjc[i]=1ll*mjc[i-1]*(m-n-1+i)%mod;
	inv[n<<1|1]=qpow(jc[n<<1|1],mod-2);minv[n<<1|1]=qpow(mjc[n<<1|1],mod-2);
	for(int i=2*n;i>=1;i--)inv[i]=1ll*inv[i+1]*(i+1)%mod,minv[i]=1ll*minv[i+1]*(m-n+i)%mod;
	get(n<<1);
	for(int i=0;i<=n;i++){
		f[i]=1ll*f[i]*inv[i]%mod*inv[n-i]%mod;
		if(n-i&1)f[i]=sub(0,f[i]);
	}
	for(int i=0;i<=(n<<1);i++)g[i]=1ll*minv[i+1]*mjc[i]%mod;
	DIF(f,wl);DIF(g,wl);mul(f,g,wl);DIT(f,wl);
	for(int i=n;i<=(n<<1);i++){
		g[i-n]=1ll*mjc[i+1]*minv[i-n]%mod*f[i]%mod;
	}
    for(int i=n+1;i<=wl;i++)g[i]=0;
    for(int i=0;i<wl;i++)f[i]=0;
}

下降幂多项式乘法

考察点值的 \(\rm EGF\) ：

\[\begin{aligned} F(n)&=\sum_{i=0}\frac{f(i)}{i!}x^i\\ &=\sum_{i=0}\frac{x^i}{i!}\sum_{j=0}f_ji^{\underline j}\\ &=\sum_{j=0}f_j\sum_{i=0}\frac{i^{\underline j}}{i!}x^i\\ &=\sum_{j=0}f_j\sum_{i=0}\frac1{(i-j)!}x^i\\ &=\sum_{j=0}f_jx^j\sum_{i=0}\frac1{i!}x^i\\ &=e^xf(x) \end{aligned} \]

所以转点值表示直接卷个 \(e^x\) 。转回来卷个 \(e^{-x}\) 。注意卷了以后是 \(2n\) 阶的多项式所以数组开四倍。

void fdt(int a[],int n,int tp){
    for(int i=0;i<n;i++){
        if((tp^1)&&(i&1))e[i]=mod-inv[i];
        else e[i]=inv[i];
    }
    get(n<<1);
    for(int i=n;i<wl;i++)e[i]=0;
    ntt(a,wl,1);ntt(e,wl,1);
    for(int i=0;i<wl;i++)a[i]=1ll*a[i]*e[i]%mod;
    ntt(a,wl,-1);
    for(int i=n;i<wl;i++)a[i]=0;
}
for(int i=0;i<n+m-1;i++)a[i]=1ll*a[i]*b[i]%mod*jc[i]%mod;

多项式三角函数

考虑使用欧拉公式展开三角函数：

\[\sin F(x)=\frac{e^{\text iF(x)}-e^{-\text iF(x)}}{2\text i} \]

\[\cos F(x)\frac{e^{\text iF(x)}+e^{-\text iF(x)}}2 \]

然后关于 \(\text i\) ，可以直接变成 \(\sqrt{-1}=\sqrt{998244353-1}\) 。

void getsin(int n,int a[],int b[],int type){
    for(int i=0;i<n;i++)a[i]=1ll*a[i]*I%mod,b[i]=mod-a[i];
    getexp(n,a,expa);getexp(n,b,expb);
    if(type==1){//cos
        const int inv2=(mod+1)>>1;
        for(int i=0;i<n;i++)b[i]=1ll*(expa[i]+expb[i])*inv2%mod;
    }
    else{//sin
        const int invI=qpow(2*I%mod,mod-2);
        for(int i=0;i<n;i++)b[i]=1ll*(expa[i]-expb[i]+mod)*invI%mod;
    }
}

多项式反三角函数

考虑先求导再积分：

\[\frac{\text d}{\text dx}\arcsin F(x)=\frac{F'(x)}{\sqrt{1-F^2(x)}} \]

\[\arcsin F(x)=\int\frac{F'(x)}{\sqrt{1-F^2(x)}}\text dx \]

\[\frac{\text d}{\text dx}\arcsin F(x)=-\frac{F'(x)}{\sqrt{1-F^2(x)}} \]

\[\arcsin F(x)=-\int\frac{F'(x)}{\sqrt{1-F^2(x)}}\text dx \]

\[\frac{\text d}{\text dx}\arctan F(x)=\frac{F'(x)}{1+F^2(x)} \]

\[\arctan F(x)=\int\frac{F'(x)}{1+F^2(x)}\text dx \]

依题意模拟即可。

void getarc(int n,int a[],int b[],int type){
    get(n<<1);
    for(int i=0;i<n;i++)b[i]=a[i];
    ntt(b,wl,1);
    for(int i=0;i<wl;i++)b[i]=1ll*b[i]*b[i]%mod;
    ntt(b,wl,-1);
    for(int i=n;i<wl;i++)b[i]=0;
    if(type==0||type==1){//0 sin 1 cos
        b[0]=(mod-b[0]+1)%mod;
        for(int i=1;i<n;i++)b[i]=mod-b[i];
        getsqrt(n,b,sq);
        for(int i=0;i<n;i++)b[i]=0;
        getinv(n,sq,b);
        dao(a,n);
        get(n<<1);
        ntt(a,wl,1);ntt(b,wl,1);
        for(int i=0;i<wl;i++)b[i]=1ll*a[i]*b[i]%mod;
        ntt(b,wl,-1);
        jifen(b,n);
        if(type==1){
            for(int i=1;i<n;i++)b[i]=mod-b[i];
        }
    }
    else{
        b[0]++;
        getinv(n,b,inv);
        dao(a,n);
        get(n<<1);
        ntt(a,wl,1);ntt(inv,wl,1);
        for(int i=0;i<wl;i++)b[i]=1ll*a[i]*inv[i]%mod;
        ntt(b,wl,-1);
        jifen(b,n);
    }
}

跑的快的板子

只有板子，所以原理部分直接滚蛋。

先把一些小的函数和宏定义放在这。

const int mod=998244353;
#define add(x,y) (x+y>=mod?x+y-mod:x+y)
#define sub(x,y) (x<y?x-y+mod:x-y)
#define mul(f,g,n) for(int i=0;i<n;i++)f[i]=1ll*f[i]*g[i]%mod
void get(int n){wl=1;while(wl<n)wl<<=1;}
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=1ll*ans*a%mod;
		a=1ll*a*a%mod;
		b>>=1;
	}
	return ans;
}

首先是 NTT。不觉得 1.3s 的 NTT 太 tm 慢了吗……于是改了一发。

参考了 yhx-12243 的 NTT 实现。把指针改成了数组，没有用 unsigned long long 优化。

void init(int n){
	int t=1;
	while((1<<t)<n)t++;
	t=min(t-1,21);
	w[0]=1;w[1<<t]=qpow(31,1<<21-t);
	for(int i=t;i;i--)w[1<<i-1]=1ll*w[1<<i]*w[1<<i]%mod;
	for(int i=1;i<(1<<t);i++)w[i]=1ll*w[i&(i-1)]*w[i&-i]%mod;
}
void DIF(int a[],int n){
	for(int mid=n>>1;mid>=1;mid>>=1){
		for(int i=0,k=0;i<n;i+=mid<<1,k++){
			for(int j=0;j<mid;j++){
				int x=1ll*a[i+j+mid]*w[k]%mod;
				a[i+j+mid]=sub(a[i+j],x);
				a[i+j]=add(a[i+j],x);
			}
		}
	}
}
void DIT(int a[],int n){
	for(int mid=1;mid<n;mid<<=1){
		for(int i=0,k=0;i<n;i+=mid<<1,k++){
			for(int j=0;j<mid;j++){
				int x=a[i+j+mid];
				a[i+j+mid]=1ll*sub(a[i+j],x)*w[k]%mod;
				a[i+j]=add(a[i+j],x);
			}
		}
	}
	int inv=qpow(n,mod-2);
	for(int i=0;i<n;i++)a[i]=1ll*a[i]*inv%mod;
	reverse(a+1,a+n);
}
void Mul(int a[],int b[],int n,int m,int c[]){
	static int A[300010],B[300010];
	get(n+m);
	for(int i=0;i<n;i++)A[i]=a[i];
	for(int i=0;i<m;i++)B[i]=b[i];
	DIF(A,wl);DIF(B,wl);mul(A,B,wl);DIT(A,wl);
	for(int i=0;i<n+m-1;i++)c[i]=add(c[i],A[i]);
	for(int i=0;i<wl;i++)A[i]=B[i]=0;
}

这玩意具体是个什么东西可以看这篇博客，讲的很清楚。

稍微说一下就是 DIF-DIT 这种东西可以省掉蝴蝶变换，然后这个预处理原根是蝴蝶变换之后的原根，可以使移动原根的次数从 \(O(n\log n)\) 变成 \(O(n)\)。

关于预处理的数字在模数不同时情况的问题，进一步的，我在询问博主本人并本机测试之后得到结论：设 NTT 模数为 \(r\times 2^k+1\)，那么这个预处理的数（\(31\)）应当是 \(g^r\)，同时 \(t\) 的阈值（\(21\)）应当是 \(k-2\)。

然后是多项式全家桶运算。其实需要优化的就四个基本的。

多项式乘法逆

参考论文哥博客的优化。

首先都 3202 年了相信大部分人都知道牛顿迭代不用递归了。

然后事实上只需要循环卷积优化和复用点值的优化就可以跑到 300ms 以内。

其实也可以看 cmd 的博客，有一份比较良好的实现，但是没有复用点值的优化。

void getinv(int n,int f[],int g[]){
    get(n);
    static int tmp[300010],ret[300010];
    g[0]=qpow(f[0],mod-2);
    for(int len=2;len<=wl;len<<=1){
        memcpy(tmp,f,4*len);memcpy(ret,g,2*len);
        DIF(tmp,len);DIF(ret,len);mul(tmp,ret,len);
        DIT(tmp,len);
        memset(tmp,0,2*len);tmp[0]=mod-1;
        DIF(tmp,len);mul(ret,tmp,len);
        DIT(ret,len);
        for(int i=len>>1;i<len;i++)g[i]=mod-ret[i];
    }
	for(int i=n;i<wl;i++)g[i]=0;
	for(int i=0;i<wl;i++)tmp[i]=ret[i]=0;
}

多项式对数函数

还是朴素的求逆乘一下。没看懂论文哥博客里的东西。

void dao(int f[],int n){
	for(int i=1;i<n;i++)f[i-1]=1ll*f[i]*i%mod;
	f[n-1]=0;
}
void jifen(int f[],int n){
	for(int i=n;i>=1;i--)f[i]=1ll*f[i-1]*inv[i]%mod;
	f[0]=0;
}
void getln(int n,int f[],int g[]){
    getinv(n,f,g);get(n<<1);
	for(int i=n;i<wl;i++)f[i]=g[i]=0;
    dao(f,wl);
    DIF(f,wl);DIF(g,wl);mul(g,f,wl);
    DIT(g,wl);
    jifen(g,wl);
	for(int i=n;i<wl;i++)g[i]=0;
}

多项式指数函数

别老惦记着牛顿迭代了。慢死了。

采用半在线卷积的方式。半在线卷积的板子已经写过，给个暴力的实现和接口。

void bruteexp(int f[],int g[],int l,int r){
	if(!l)f[l]=1;
	else f[l]=1ll*f[l]*inv[l]%mod;
	for(int i=l+1;i<=r;i++){
		for(int j=l;j<i;j++){
			int x=1ll*f[j]*g[i-j]%mod;
			f[i]=add(f[i],x);
		}
		f[i]=1ll*f[i]*inv[i]%mod;
	}
}
void getexp(int n,int f[],int g[]){
	for(int i=0;i<n;i++)f[i]=1ll*f[i]*i%mod;
	solve(g,f,n,bruteexp);
}

多项式开根

使用了论文哥的方法。看的时候看的不是很懂，所以给出一个实现，可以对着实现参考一下理解。

void getsqrt(int n,int f[],int g[]){
	get(n);
	const int inv2=(mod+1)>>1;
	static int tmp[300010],ret[300010],h[300010],g2[300010],ans[300010];
	g[0]=g2[0]=Cipolla::get(f[0]);h[0]=qpow(g[0],mod-2);
	for(int len=2;len<=wl;len<<=1){
		for(int i=0;i<(len>>1);i++)tmp[i]=h[i],ret[i]=1ll*g2[i]*g2[i]%mod;
		DIT(ret,len>>1);
		for(int i=0;i<(len>>1);i++)ans[i+(len>>1)]=sub(sub(ret[i],f[i]),f[i+(len>>1)]),ans[i]=0;
		DIF(ans,len);DIF(tmp,len);
		for(int i=0;i<len;i++)ans[i]=1ll*ans[i]*tmp[i]%mod*inv2%mod;
		DIT(ans,len);
		for(int i=len>>1;i<len;i++)g[i]=sub(0,ans[i]);
		if(len!=wl){
			for(int i=0;i<len;i++)ret[i]=g[i];
			DIF(ret,len);
			for(int i=0;i<len;i++)g2[i]=ret[i],ret[i]=1ll*ret[i]*tmp[i]%mod;
			DIT(ret,len);
			for(int i=1;i<(len>>1);i++)ret[i]=0;ret[0]=mod-1;
			DIF(ret,len);mul(ret,tmp,len);DIT(ret,len);
			for(int i=len>>1;i<len;i++)h[i]=sub(0,ret[i]);
		}
	}
}