二维计算几何基础
大概是大多数基础的部分，顺便附上长篇大论的结构体封装。
如果whk有不懂的建议先搞懂whk的几何部分。
感谢lin4xu老师的计算几何板子。快去给我关注（
图形的记录
- 点/向量：直接记录坐标。
- 线：直线记录直线上一点和方向向量。线段记录两个端点。曲线记录函数解析式。
- 多边形：按顺/逆时针记录每个顶点的坐标。
向量
以下向量均用\(\vec a,\vec b\)表示。
- 点积：\(\vec a\cdot \vec b=x_ax_b+y_ay_b\)
这个可以用来判断两个向量的前后关系。
- 叉积：\(\vec a \times \vec b=x_ay_b-x_by_a\)
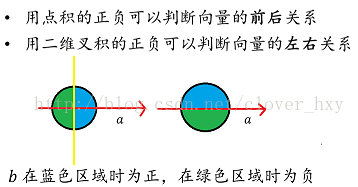
这个用的多，可以用来判断两个向量的左右关系。具体的我来盗个图。左边是点积，右边是叉积。学校可能看不见图，建议打开源码。
3. 向量旋转：我们图个直观先放到极坐标系里。
设原向量是\((r\cos A,r\sin A)\)，我们现在要将它逆时针旋转角度\(B\)，则现在的向量就是
然后我们套到平面直角坐标系里，用\(x\)替换\(r\cos A\)，用\(y\)替换\(r\sin A\)，就变成了
- 极角排序
cmath库中\(\text{atan2}(y,x)\)求的是\(\arctan \frac yx\)。我们就可以轻松地求出极角然后排序。
于是我们现在就有了一个基本算是全的封装好的向量结构体。
const double eps=1e-8;
struct node{
double x,y;
node operator-(){return node{-x,-y};}//取反
node operator+(const node &s)const{return node{x+s.x,y+s.y};}
node operator-(const node &s)const{return (node){x-s.x,y-s.y};}//加减
node operator*(const double a)const{return (node){x*a,y*a};}
node operator/(const double a)const{return (node){x/a,y/a};}//数乘
node operator+=(node s){x+=s.x;y+=s.y;return *this;}
node operator-=(node s){x-=s.x;y-=s.y;return *this;}
node operator*=(double a){x*=a;y*=a;return *this;}
node operator/=(double a){x/=a;y/=a;return *this;}
double operator*(node s){return x*s.x+y*s.y;}//点积
double operator^(node s){return x*s.y-y*s.x;}//叉积
double len(){return sqrt(x*x+y*y);}//模长
node operator&(const double &a)const{
double cs=cos(y),sn=sin(y);
return (node){cs*x-sn*y,sn*x+cs*y};//逆时针旋转角度a
}
};
bool cmp1(node a,node b){return fabs(a.x-b.x)<=eps?a.y<b.y:a.x<b.x;}//坐标序
bool cmp2(node a,node b){return atan(a.y,a.x)<atan(b.y,b.x);}//极角序
直线与线段
- 判断点在直线哪边：直接拿直线上一个点和该点的向量和直线的方向向量叉乘一下就行。形式化的，设\(P\)为直线上一点，\(Q\)为直线外一点，直线方向向量为\(\vec l\)。若\(\overrightarrow {PQ}\times \vec l>0\)则在直线右侧，反之在左侧。
- 两直线夹角：\(\theta=\text{atan2}(\vec x\times \vec y,\vec x \cdot \vec y)\)。直接把点积和叉积拆开即可得到。
- 点线距：直接算个叉积然后除以边长就是了。这个whk都会吧。
- 线段是否相交
这里要介绍一下两个东西：快速排斥实验和跨立实验。首先是快速排斥实验。这个用来排除那种“一眼看上去就离得很远”的那种线段。让我继续盗图。
举个例子，我们有这两条线段：
图中标出了线段和它们占用的空间。一眼看上去它们的占用空间就不相交，所以直接排除。这就是快速排斥实验。
然后是跨立实验。如果线段\(a,b\)相交，则\(b\)的两个端点一定在\(a\)两端，同理，\(a\)的两端点也一定在\(b\)两端。所以我们可以看两端点与另一直线的位置关系。这个可以用叉积表示。具体地说，我们设两线段端点分别为\(a_1,a_2,b_1,b_2\)，若\((b_1-a_1)\times (b_1-a_2)\)和\((b_2-a_1)\times (b_2-a_2)\)不同号，且\((a_1-b_1)\times (a_1-b_2)\)和\((a_2-b_1)\times (a_2-b_2)\)不同号，则两线段相交。这就是跨立实验。
注意到我们需要特判两线段共线的情况。如果不需要这个性质只做跨立实验就可以了。但是如果需要特判共线则需要把跨立实验的\(<0\)改成\(\le 0\)并加上快速排斥实验（判断共线但不相交）。
当然你也可以算个交点然后点积判一下位置关系……
- 直线/线段交点
首先上个图然后给证明。看不见的同样请扒源码。
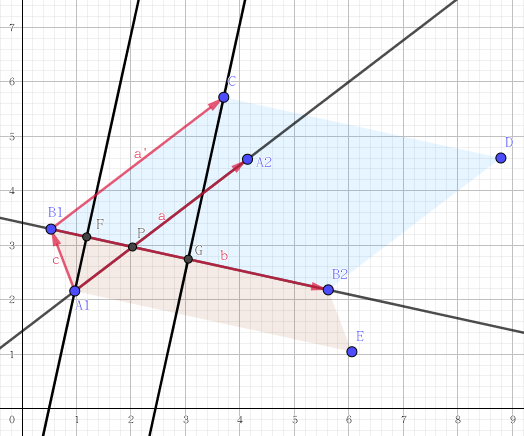
首先我们现在要找线段\(A_1A_2,B_1B_2\)的交点\(P\)。我们先作\(A_1F\bot B_1B_2\)于点\(F\),然后平移向量\(\vec a\)（即\(\overrightarrow {A_1A_2}\)）到\(\overrightarrow {B_1C}\)的位置，过点\(C\)作\(CG\bot B_1B_2\)于点\(G\)。
考虑向量叉积的几何意义，是以两向量为邻边的平行四边形面积。所以我们现在可以用叉积算出\(\frac {S_{B_1B_2DC}}{S_{A_1B_1B_2E}}\)的值。而由于两个平行四边形的底相等，所以可以把底除掉，剩下\(\frac {CG}{A_1F}\)。而我们发现\(\angle A_1PB_1=\angle PB_1C\)，则\(\bigtriangleup A_1PF \sim \bigtriangleup CB_1G\)，则\(\frac {CG}{A_1F}=\frac{B_1C}{A_1P}=\frac {A_1A_2}{A_1P}\)。直接算个数乘就行了。
仍然放上封装好的结构体：
struct line{
node x,y;//起点终点
double angle;//极角
bool operator&(const line &s){
return ((s.y-x)^(y-x))*((s.x-x)^(y-x))<0&&((y-s.x)^(s.y-s.x))*((x-s.x)^(s.y-s.x))<0;
}//跨立实验判断线段相交
friend bool operator<(const node &x,const line &y){
return (x-y.x^y.y-y.x)<0;//点是否在线左侧
}
friend bool operator<(const line &x,const line &y){
return abs(x.angle-y.angle)<=eps?x.x<y.x:x.angle<y,angle;//极角序
}
friend bool operator>(const node&x,const line &y){return !(x<y);}
friend double operator*(const line&x,const node &y){
return abs(y-x.x^y-x.y)/!(x.y-x.x);//点线距
}
friend node operator*(const line &x,const line &y){
return x.x+(x.y-x.x)*(x.x-y.x^y.y-y.x)/(y.y-y.x^x.y-x.x);//直线交点
}
};
多边形
- 判断一点是否在多边形内部
首先我们从该点向正右方引一条射线，然后统计这条射线与多边形的交点个数。奇数则在内部，偶数则在外部。然后是正好经过顶点的情况，判断纵坐标是否相同，相同直接忽略。
- 求多边形面积
我们曾经有一个把多边形三角剖分以后求三角形面积和的法子，但是那个太复杂了，现在我们需要一个更简洁的方法。还记的叉积的几何意义吗？叉积大小是以两向量为邻边的平行四边形的面积大小。所以我们可以直接将所有点按极角排序之后以随便某个点为起点两两算个叉积，最后由于我们是算的三角形，但是按照平行四边形算了，所以要除以\(2\)。
double area(node a[],int n){
double ans=0;
for(int i=3;i<=n;i++)ans+=(q[i-1]-q[1])^(q[i]-q[1]);
return ans/2;
}
- 判定一个点是否在凸包内部
首先判是否在边界上，然后找到与其极角相邻的两个点判断（需要\(a[1]=(0,0)\)，如果凸包不满足要转换一下坐标）。
bool in(node q[],int n,node x){
if((x-q[1])^(q[n]-q[1])<0||(x-q[1]^(q[2]-q[1])>0))return false;
int pos=lower_bound(q+2,q+t+1,[](const node &x,const node &y){
double tmp=x-q[1]^y-q[1];
return abs(tmp)<=eps?!(x-q[1])<!(y-q[1]):tmp>0;//极角序排序 找极角相邻的两个点
})-q-1;
return (x-q[pos]^q[pos+1]-q[pos])<=0;
}
圆
- 求直线与圆交点
首先算个圆心和直线距离判断一下位置关系。如果相离直接没有，相切可以直接勾股定理算交点，相交可以勾股算出两个交点的中点（有斜边：半径，一条直角边：圆心到直线距离）然后数学怎么算这个怎么算就行。
- 两圆交点
还是算圆心距离判一下位置关系。如果外离（\(O_1O_2>R_1+R_2\)）或内含（\(O_1O_2<\min(R_1,R_2)\)）直接没有。如果相切也好算，一眼就能出就不多说了。如果相交则有两个交点，且关于圆心连线对称。我们将两个圆心与任意一个交点相连（另一个交点在算出这一个之后对称一下就行了），然后知道三边，我们就可以求出两个圆心和一个交点组成的这个三角形中圆心连线与交点成角的大小，也就知道了方向向量。于是求就好了。
最后是一些注意事项：
- 注意精度。
- 注意卡常。
