WQS二分（凸完全单调性优化dp）
wqs二分是巨佬王钦石在2012年论文中提出的一种二分方法。或者叫做带权二分。或者叫dp凸优化，一般用于\(n\)选\(m\)求最小权值一类的问题。这类问题一般有两个特点：
- 复杂度一般都是\(O(nm)\)及以上，不能接受。
- 如果把这个限制\(m\)的条件去了那就很水。
其实主要是你觉得这个题能用那就能用（
既然叫凸优化，那么它就只使用于答案构成一个凸包的问题。首先手搓一个题举例子。
\(n\)个物品，每个都有权值，以某种方式计算权值，要求权值最大，选的方式和选哪些物品都会影响权值。
首先我们有一个相当显然的dp：设\(dp[i][j]\)为到第\(i\)个，选了\(j\)个的最大权值，那么有
于是这个是\(O(nm)\)的，看上去就很退化。然后看把\(m\)去了会怎样，发现可以直接单调队列\(O(n)\)搞。事实上如果你打个表会发现\(dp[n][1]\)到\(dp[n][m]\)是个上凸包，于是考虑wqs二分。（我来盗个图）
如图，我们有这样一个凸包。
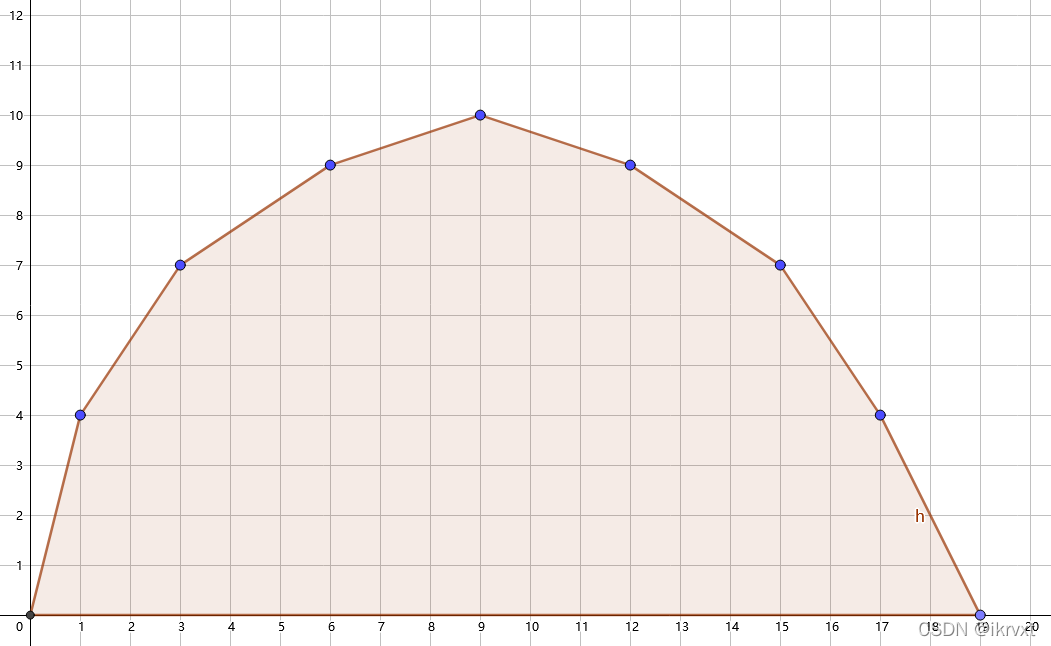
然后我们用一条直线来切这个凸包，直到切到我们想要的\(m\)位置的最大值。
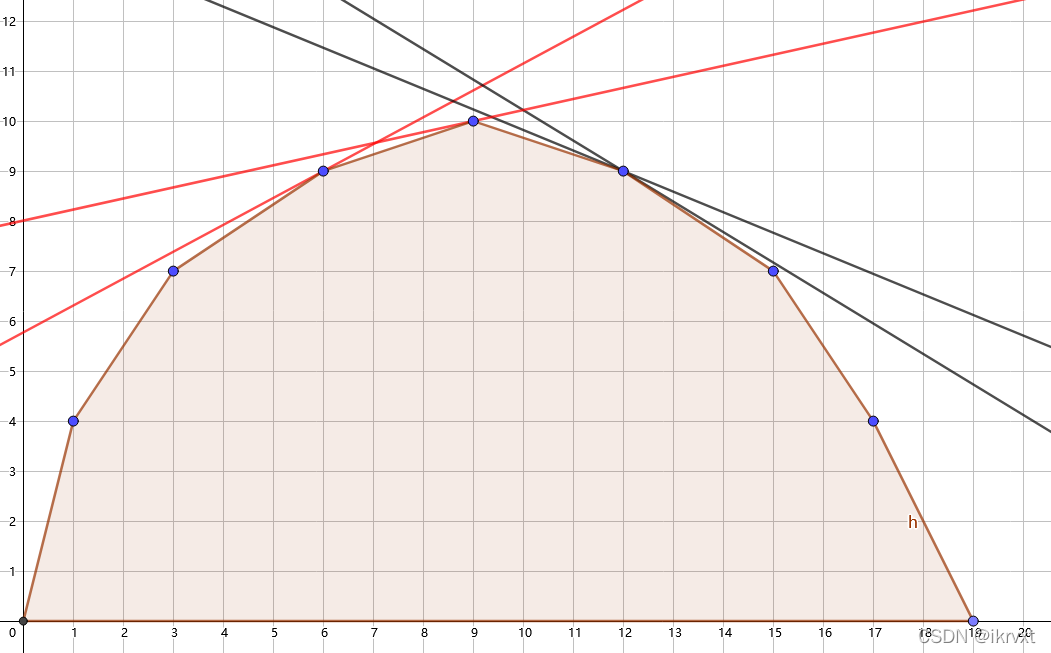
大体过程就是这样，每次二分判断当前答案是否合法（就是\(x\)是否满足条件）。然后是这样一个问题：我们现在知道了斜率，那么如何求出最大值？
假如说这条直线是\(y=kx+b\)，我们现在可以dp一次，从而知道了\(y\)的值。而\(x\)就是我们选择的数量，即\(m\)。\(k\)又是已知量，所以最大值\(b\)就有了。
然后是注意事项。非常重要。
二分最后一定要减去\(m\times k\)，而不是你最后check出的答案\(mid\)乘\(k\)或直接不重新跑一遍斜率直接输出答案。
为什么？考虑这样一种情况：
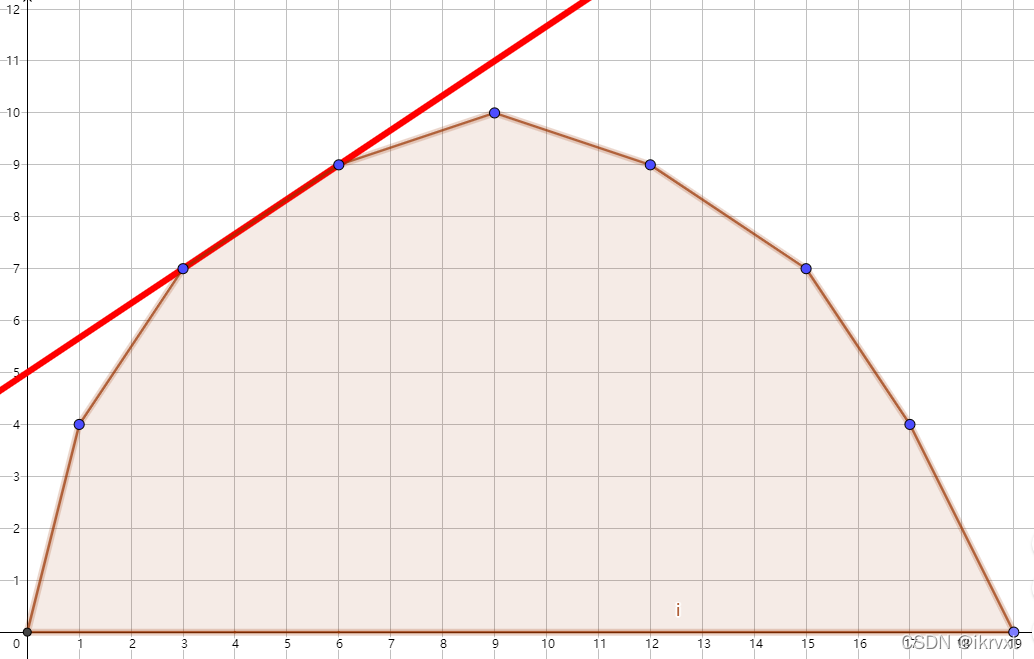
你的一条直线同时切到了一堆点。而如果你\(m\)在中间，而减去\(mid\)计算答案，那么答案显然是错的。怎么做？小数二分？怒T。
实际上，我们不需要精确得到我们最后的斜率，因为最后减掉了。我们可以在每次\(\ge m\)时接受答案，因为这一大段上的斜率都是一样的。
然后上题：Tree I
题意：\(n\)个点\(m\)条边，有白边和黑边，求有\(need\)条白边的最小生成树。
直接套路wqs二分。每次二分一个权值给白边加上，然后最小生成树，最后回代一下斜率就行了。然后，这个题在黑白边相同的时候，你有两种选择：选黑或白。这时（还是用上面那张图）：
如果你选白边，那么最后切出来的点是\(\ge m\)的，要在\(mid\ge m\)时转移答案。
如果你选黑边，那么最后切出来的点是\(\le m\)的，要在\(mid \le m\)时转移答案。
int main(){
scanf("%d%d%d",&n,&m,&nd);
for(int i=1;i<=m;i++){
int u,v,w,col;scanf("%d%d%d%d",&u,&v,&w,&col);
edge[i]={u,v,w,col};
if(col==0)swap(edge[++cnt],edge[i]);
}
sort(edge+1,edge+cnt+1);sort(edge+cnt+1,edge+m+1);
int l=-100,r=100;//注意因为这个题斜率有负数所以要-100
while(l<r){
int mid=(l+r+1)>>1,ans=0,i=1,j=cnt+1;
for(int i=0;i<n;i++)fa[i]=i;
for(i=1,j=cnt+1;i<=cnt&&j<=m;){
edge[i].w+mid<=edge[j].w?ans+=add(i++):add(j++);//优先选白边加入
}
while(i<=cnt)ans+=add(i++);
if(ans<nd)r=mid-1;
else l=mid;
}
int mid=l;//最后回代斜率
for(int i=0;i<n;i++)fa[i]=i;
int ans=0,i=1,j=cnt+1;
while(i<=cnt&&j<=m){
if(edge[i].w+mid<=edge[j].w)ans+=(edge[i].w+mid)*add(i),i++;
else ans+=edge[j].w*add(j),j++;
}
while(i<=cnt)ans+=(edge[i].w+mid)*add(i),i++;
while(j<=m)ans+=edge[j].w*add(j),j++;
printf("%d",ans-nd*mid);
}
忘情
题意：\(n\)个数分\(m\)段，每段权值为\((\sum a_i+1)^2\)，求权值和的最小值。
首先如果没有这个\(m\)显然可以斜率优化。然后我们加上\(m\)，考虑wqs二分。每次给一段附带一个权值\(val\)，即权值为\((\sum a_i+1)^2+val\)。然后跑普通的斜率优化记录答案。
int y(int x){
return dp[x]+s[x]*s[x]-2*s[x];
}
double slope(int x1,int x2){
return 1.0*(y(x2)-y(x1))/(1.0*s[x2]-s[x1]);
}
bool check(int val){
int l=1,r=1;
for(int i=1;i<=n;i++){
while(l<r&&slope(q[l],q[l+1])<=2*s[i])l++;
dp[i]=dp[q[l]]+(s[i]-s[q[l]]+1)*(s[i]-s[q[l]]+1)+val;
cnt[i]=cnt[q[l]]+1;
while(l<r&&slope(q[r-1],q[r])>=slope(q[r],i))r--;
q[++r]=i;
}//斜率优化板子
return cnt[n]>=m;//我是在>=m时记录答案的 因为斜率优化的时候记录的是当前斜率最大的数 可能比m大所以要>=m
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++){
int a;scanf("%lld",&a);
s[i]=s[i-1]+a;
}
int l=0,r=1e15,ans;
while(l<r){
int mid=(l+r)>>1;
if(check(mid))l=mid+1,ans=mid;
//这个题求最小值 是上凸包 如果答案超过m就记录顺便增大斜率来使切点横坐标减小 反之增大
else r=mid;
}
check(ans);
printf("%lld",dp[n]-m*ans);
return 0;
}
后记：这个东西是我在写这篇博客顺便给joke3579调代码的时候突然“我逐渐理解一切”的。
